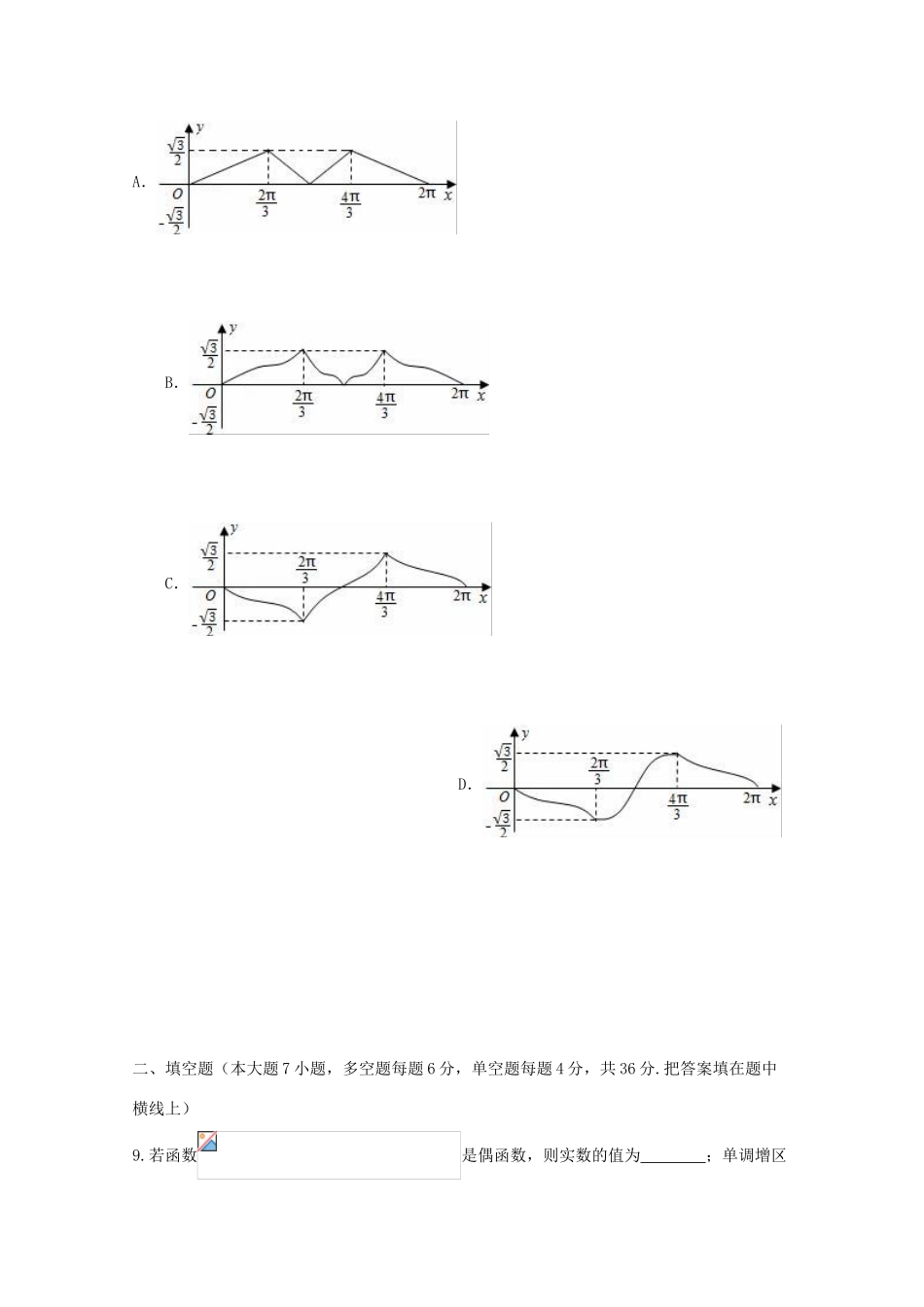
2017浙江省高考压轴卷数学(文)球的表面积公式球的体积公式其中R表示球的半径柱体的体积公式其中S表示柱体的底面积,h表示柱体的高椎体的体积公式其中S表示椎体分底面积,h表示椎体的高台体的体积公式其中分别表示台体的上、下底面面积,h表示台体的高一、选择题(本大题10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知全集U=R,集合A={x|2x<1},B={x|log3x>0},则A∩(∁UB)=()A.{x|x>1}B.{x|x>0}C.{x|0<x<1}D.{x|x<0}2.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积为()A.B.C.D.3.已知实数{an}是等比数列,若a2a5a8=8,则a1a9+a1a5+a5a9()A.有最小值12B.有最大值12C.有最小值4D.有最大值44.已知命题p:∃x0∈R,x02+2x0+1≤0,则¬p为()A.∃x0∈R,x02+2x0+1>0B.∀x∈R,x2+2x+1≤0C.∀x∈R,x2+2x+1≥0D.∀x∈R,x2+2x+1>05.已知双曲线C:﹣=1(a>0,b>0)的左、右焦点分别为F1,F2,过F2作平行于C的渐近线的直线交C于点P.若PF1⊥PF2,则C的离心率为()A.B.C.2D.6.已知实数x,y满足约束条件且目标函数z=2x+y的最大值是6,最小值是1,则的值是()A.1B.2C.3D.47.已知直线ax+by=1(其中a,b为非零实数)与圆x2+y2=1相交于A,B两点,O为坐标原点,且△AOB为直角三角形,则+的最小值为()A.2B.3C.4D.58.如图,正△ABC的中心位于点G(0,1),A(0,2),动点P从A点出发沿△ABC的边界按逆时针方向运动,设旋转的角度∠AGP=x(0≤x≤2π),向量在=(1,0)方向的射影为y(O为坐标原点),则y关于x的函数y=f(x)的图象是()A.B.C.D.二、填空题(本大题7小题,多空题每题6分,单空题每题4分,共36分.把答案填在题中横线上)9.若函数是偶函数,则实数的值为;单调增区间为.10.已知f(x)=lg(2x﹣4),则方程f(x)=1的解是,不等式f(x)<0的解集是.11.已知平面向量,若,则=,若,则=;12.直线ax+by=1与圆x2+y2=1相交于A,B两点,若△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(2,2)之间距离的最小值为,最大值.13.已知F1、F2分别为双曲线(a>0,b>0)的左、右焦点,若在右支上存在点A,使得点F2到直线AF1的距离为2a,则该双曲线的离心率的取值范围是.14.已知函数f(x)的定义域为R,若存在常数m>0,对任意x∈R,有|f(x)|≤m|x|,则称函数f(x)为F﹣函数.给出下列函数:①f(x)=x2;②f(x)=;③f(x)=2x;④f(x)=sin2x.其中是F﹣函数的序号为.15.某同学的作业不小心被墨水玷污,经仔细辨认,整理出以下两条有效信息:①题目:“在平面直角坐标系中,已知椭圆的左顶点为,过点作两条斜率之积为2的射线与椭圆交于,…”②解:“设的斜率为,…点,,…”据此,请你写出直线的斜率为.(用表示)三、解答题(本大题共5小题迷宫74分.解答应写出文字说明,证明过程或演算步骤)16.在△ABC中,a,b,c分别为内角A,B,C的对边,且2cos(B﹣C)=4sinB•sinC﹣1.(1)求A;(2)若a=3,sin=,求b.17.数列{an}满足a1=1,(n∈N+).(1)证明:数列是等差数列;(2)求数列{an}的通项公式an;(3)设bn=n(n+1)an,求数列{bn}的前n项和Sn.18.在三棱柱ABC﹣A1B1C1中,侧面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=,设D为CC1中点,(Ⅰ)求证:CC1⊥平面A1B1D;(Ⅱ)求DH与平面AA1C1C所成角的正弦值.19.已知抛物线y2=2px,过焦点且垂直x轴的弦长为6,抛物线上的两个动点A(x1,y1)和B(x2,y2),其中x1≠x2且x1+x2=4,线段AB的垂直平分线与x轴交于点C.(1)求抛物线方程;(2)试证线段AB的垂直平分线经过定点,并求此定点;(3)求△ABC面积的最大值.20.已知函数,,(1)当时,求函数的最小值;(2)若对任意,恒成立,试求实数的取值范围.2017浙江省高考压轴卷数学(文)1.【答案】D【解析】A={x|x<0},B={x|x>1},则CUB={x|x≤1},∴A∩(∁UB)={x|x<0},故选D.2.【答案】B【解析】由三视图知该几何体是高为的三棱柱截去同底且高为的三棱锥所得几何体,体积等于,选B.3.【答案】A【解析】 {an}...