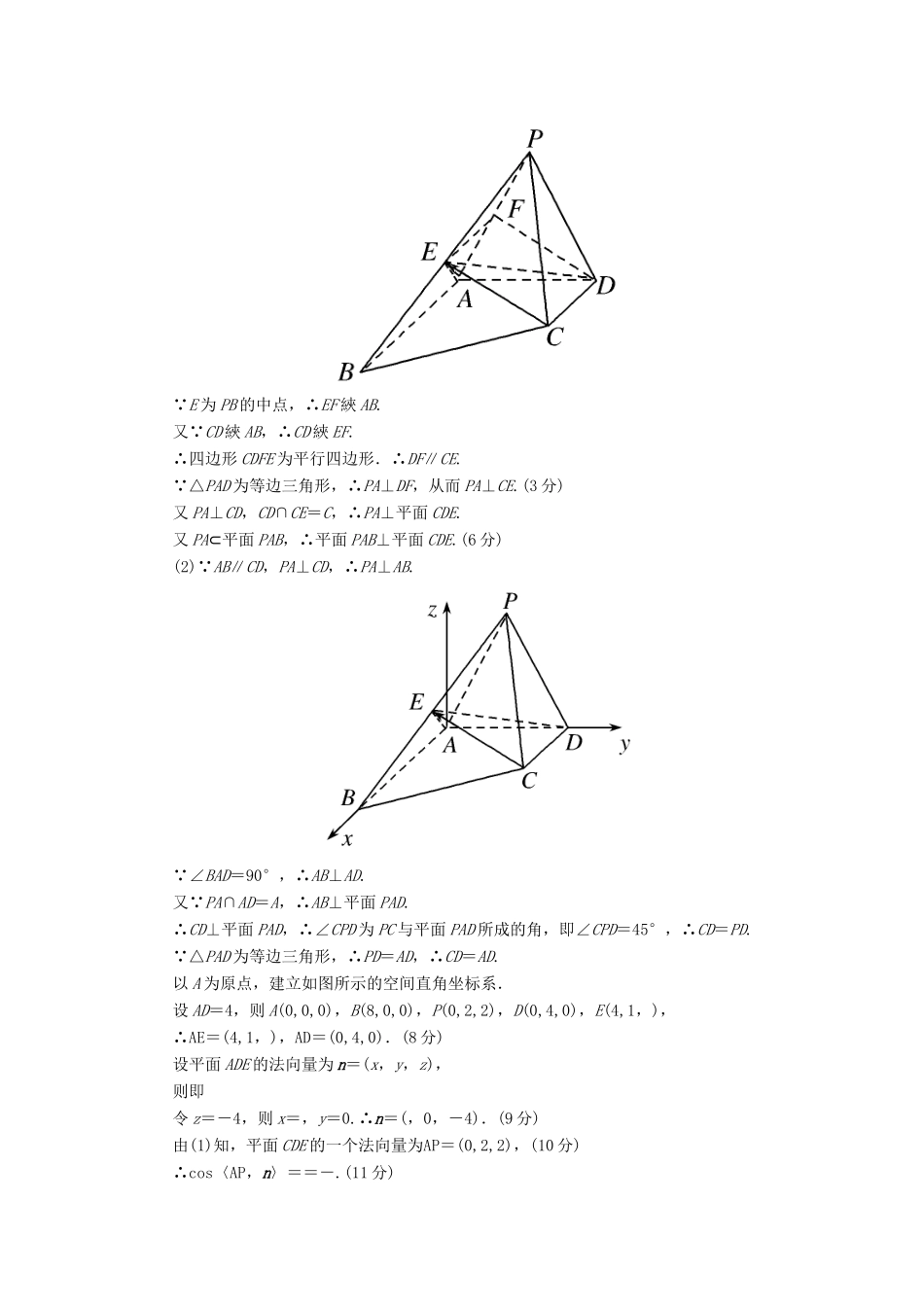
规范练(三)(时间:45分钟满分:46分)1.(12分)在△ABC中,角A,B,C的对边分别为a,b,c,且满足cos2A+cos2C-cos2B=1+sinAsinC.(1)求角B的大小;(2)若a=3,点D在AC边上且BD⊥AC,BD=,求c.[规范解答及评分标准](1)由cos2A+cos2C-cos2B=1+sinAsinC得1-sin2A+1-sin2C-(1-sin2B)=1+sinAsinC.即sin2A+sin2C-sin2B=-sinAsinC.(3分)由正弦定理得a2+c2-b2=-ac,由余弦定理得cosB==-.因为B∈(0,π),所以B=.(6分)(2)由(1)及a=3知,b2=a2+c2+ac=c2+3c+9.因为BD⊥AC,所以△ABC的面积S=acsin∠ABC=b·BD.(9分)所以×3×c×=×b×,解得b=c.所以2=c2+3c+9,解得c=5(负值已舍去).(12分)2.(12分)如图,四棱锥P—ABCD中,△PAD为等边三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点.(1)求证:平面PAB⊥平面CDE;(2)若直线PC与平面PAD所成角为45°,求二面角A—DE—C的余弦值.[规范解答及评分标准](1)证明:如图,取AP的中点为F,连接EF,DF. E为PB的中点,∴EF綊AB.又 CD綊AB,∴CD綊EF.∴四边形CDFE为平行四边形.∴DF∥CE. △PAD为等边三角形,∴PA⊥DF,从而PA⊥CE.(3分)又PA⊥CD,CD∩CE=C,∴PA⊥平面CDE.又PA⊂平面PAB,∴平面PAB⊥平面CDE.(6分)(2) AB∥CD,PA⊥CD,∴PA⊥AB. ∠BAD=90°,∴AB⊥AD.又 PA∩AD=A,∴AB⊥平面PAD.∴CD⊥平面PAD,∴∠CPD为PC与平面PAD所成的角,即∠CPD=45°,∴CD=PD. △PAD为等边三角形,∴PD=AD,∴CD=AD.以A为原点,建立如图所示的空间直角坐标系.设AD=4,则A(0,0,0),B(8,0,0),P(0,2,2),D(0,4,0),E(4,1,),∴AE=(4,1,),AD=(0,4,0).(8分)设平面ADE的法向量为n=(x,y,z),则即令z=-4,则x=,y=0.∴n=(,0,-4).(9分)由(1)知,平面CDE的一个法向量为AP=(0,2,2),(10分)∴cos〈AP,n〉==-.(11分)由图可知二面角A—DE—C的平面角为钝角,∴二面角A—DE—C的余弦值为-.(12分)3.(12分)某电商2018年计划与所在地区的樱桃果园合作进行樱桃的销售,为了了解该地区果园的樱桃销售情况,现从中随机抽取60个樱桃果园,统计各果园2017年的销售量(单位:万斤),得到下面的频率分布直方图.(1)从样本中销售量不低于9万斤的果园中随机选取3个,求销售量不低于10万斤的果园的个数X的分布列及其数学期望;(2)该电商经过6天的试运营,得到销售量(单位:万斤)的情况统计表如下:运营第n天123456第n天电商的销售量yn1.211.311.451.712.022.54根据相关性分析,前n天累计总销量Tn与n之间具有较强的线性相关关系,由最小二乘法得回归直线方程为T=1.78n+a,用样本估计总体的思想,预测该电商至少运营多少天可使总销量不低于该地区各果园2017年的平均销量的2倍.注:1.前n天累计总销售量Tn=yi.2.在频率分布直方图中,同一组数据用该区间的中点值作为代表.3.1斤=0.5千克.[规范解答及评分标准](1)由频率分布直方图可得样本中2017年销售量不低于9万斤的果园有(0.10+0.05)×60=9(个),销售量不低于10万斤的果园有0.05×60=3(个).(2分)随机变量X的可能取值为0,1,2,3.P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==,∴随机变量X的分布列为X0123P(4分)∴E(X)=0×+1×+2×+3×=1.(6分)(2)由运营期间销售量的情况统计表可得前n天累计总销售量Tn(单位:万斤)如下表:运营第n天123456前n天累计总销售量Tn1.212.523.975.687.7010.24∴n==3.5,T==5.22(万斤)(8分)将样本的中心点(3.5,5.22)代入回归直线方程T=1.78n+a,得a=-1.01,∴T=1.78n-1.01.(9分)用频率分布直方图中各区间的中点值作为代表,估计该地区2017年的平均销量为4.5×0.05+5.5×0.15+6.5×0.20+7.5×0.30+8.5×0.15+9.5×0.10+10.5×0.05=7.35(万斤).由题意,得1.78n-1.01≥14.7,解得n≥8.83(11分) n∈N*,∴该电商至少运营9天可使总销量不低于该地区各果园2017年的平均销量的2倍.(12分)选考题:共10分.请考生在第4、5题中任选一题作答.如果多做,那么按所做的第一题计分.4.[选修4-4:坐标系与参数方程](10分)已知直线l的参数方程为(t为参数).以O为极点,x轴的非...