全国名校高考数学试题分类汇编（12月 第一期）G11 空间角与距离的求法（含解析）VIP免费

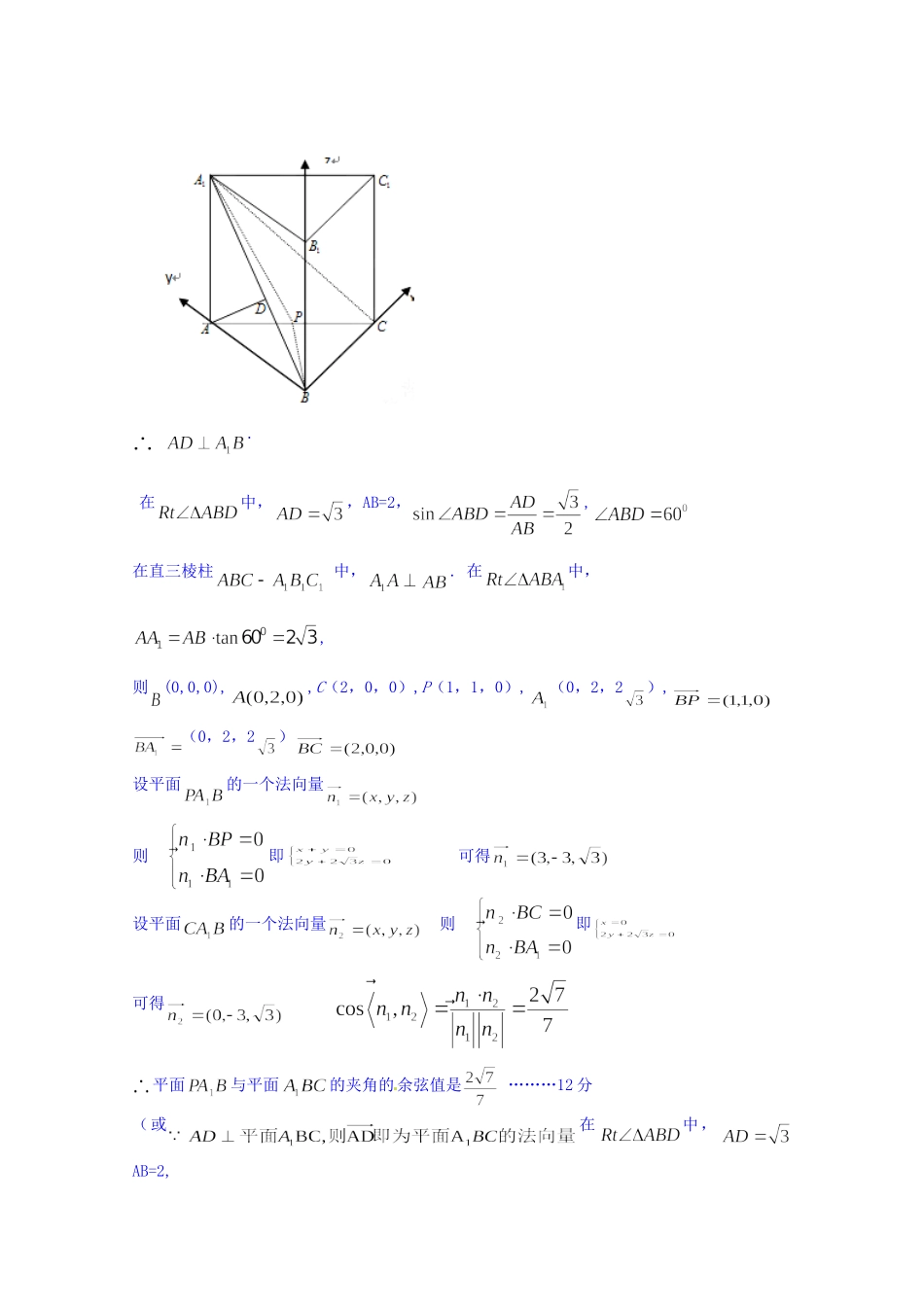
G11空间角与距离的求法【数学理卷·届河北省衡水中学高三上学期期中考试（11）】18、（本小题满分12分）如图，四棱锥中，底面为菱形，是的中点（1）若，求证：平面平面；（2）若平面平面，且，在线段上是否存在点，使二面角的大小为，若存在，试确定点M的位置，若不存在，请说明理由。【知识点】空间角与空间中的位置关系.G4,G5,G11【答案】【解析】(1)略(2)略解析：（1）证明： PA=PD，Q为AD的中点，∴PQ⊥AD，又 底面ABCD为菱形，∠BAD=60°，∴BQ⊥AD，又PQ∩BQ=Q，∴AD⊥平面PQB，又 AD⊂平面PAD，∴平面PQB⊥平面PAD．（2）解： 平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，PQ⊥AD，∴PQ⊥平面ABCD，以Q为坐标原点，分别以QA，QB，QP为x，y，z轴，建立空间直角坐标系，如图则Q（0，0，0），），B（0，设0＜λ＜1，则平面CBQ的一个法向量=（0，0，1），设平面MBQ的法向量为=（x，y，z），由， 二面角M-BQ-C的大小为60°，解得λ=，∴存在点M为线段PC靠近P的三等分点满足题意【思路点拨】1）由已知得PQ⊥AD，BQ⊥AD，由此能证明平面PQB⊥平面PAD．（2）以Q为坐标原点，分别以QA，QB，QP为x，y，z轴，建立空间直角坐标系，利用向量法能求出存在点M为线段PC靠近P的三等分点满足题意．【数学理卷·届江西省赣州市十二县（市）高三上学期期中联考（11）】19．（本小题满分12分）如图,在直三棱柱中，平面，其垂足落在直线上．（1）求证：⊥（2）若，，为的中点，求二面角的余弦值.【知识点】用空间向量求平面间的夹角；空间中直线与直线之间的位置关系．G4G5G11【答案】【解析】(1)见解析；(2)解析：(1)证明：三棱柱为直三棱柱，平面，又平面，-平面，且平面，.又平面,平面,，平面，又平面，⊥…………………………5分(2)由（1）知,如图,以B为原点建立空间直角坐标系平面，其垂足落在直线上,.在中，，AB=2，,在直三棱柱中，.在中，,则(0,0,0),,C（2，0，0）,P（1，1，0）,（0，2，2）,（0，2，2）设平面的一个法向量则即可得设平面的一个法向量则即可得平面与平面的夹角的余弦值是………12分（或在中，AB=2,则BD=1可得D(平面与平面的夹角的余弦值是………12分）【思路点拨】(1)由已知得平面，，．由此能证明．(2)由（1）知,如图,以B为原点建立空间直角坐标系，利用向量法能求出二面角的平面角的余弦值．【数学文卷·届江西省师大附中高三上学期期中考试（11）】19.（本小题12分）如图1，在直角梯形ABCD中，CDAB//，ADAB，且121CDADAB．现以AD为一边向梯形外作正方形ADEF，然后沿边AD将正方形ADEF翻折，使平面ADEF与平面ABCD垂直，M为ED的中点，如图2．（1）求证：AM∥平面BEC;（2）求证：BDEBC平面;（3）求点D到平面BEC的距离.【知识点】线面平行线面垂直点到平面的距离G4G5G11【答案】【解析】（1）略；（2）略；（3）36解析：（1）证明：取EC中点N，连结BNMN,．M在△EDC中，,MN分别为,ECED的中点，所以MN∥CD，且12MNCD．由已知AB∥CD，12ABCD，所以MN∥AB，且MNAB．所以四边形ABNM为平行四边形．所以BN∥AM．又因为BN平面BEC，且AM平面BEC，所以AM∥平面BEC．（2）在正方形ADEF中，EDAD．又因为平面ADEF平面ABCD，且平面ADEF平面ABCDAD，所以ED平面ABCD．所以EDBC．在直角梯形ABCD中，1ADAB，2CD，可得2BC．在△BCD中，2,2CDBCBD，所以222CDBCBD．所以BCBD．所以BC平面BDE．（3）：BE平面BDE,所以BCBE，所以,1222121BCBDSBCD.26322121BCBESBCE又BCEDBCDEVV，设点D到平面BEC的距离为.h则3131DESBCDhSBCE，所以36261BCEBCDSDESh，所以点D到平面BEC的距离等于36.【思路点拨】证明线面平行及线面垂直主要利用其判定定理进行证明，求点到平面的距离，若直接求距离不方便时，可利用三棱锥的等体积法求距离.【数学文卷·届四川省成都外国语学校高三11月月考（11）】18．（12分）在四棱锥中，，，点是线段上的一点，且，．（1）证明：面面；（2）求直线与平面所成角的正弦值．【知识点】面面垂直的判定；线面角的求法.G5G11【答案】【解析】（1）证明：见解析...