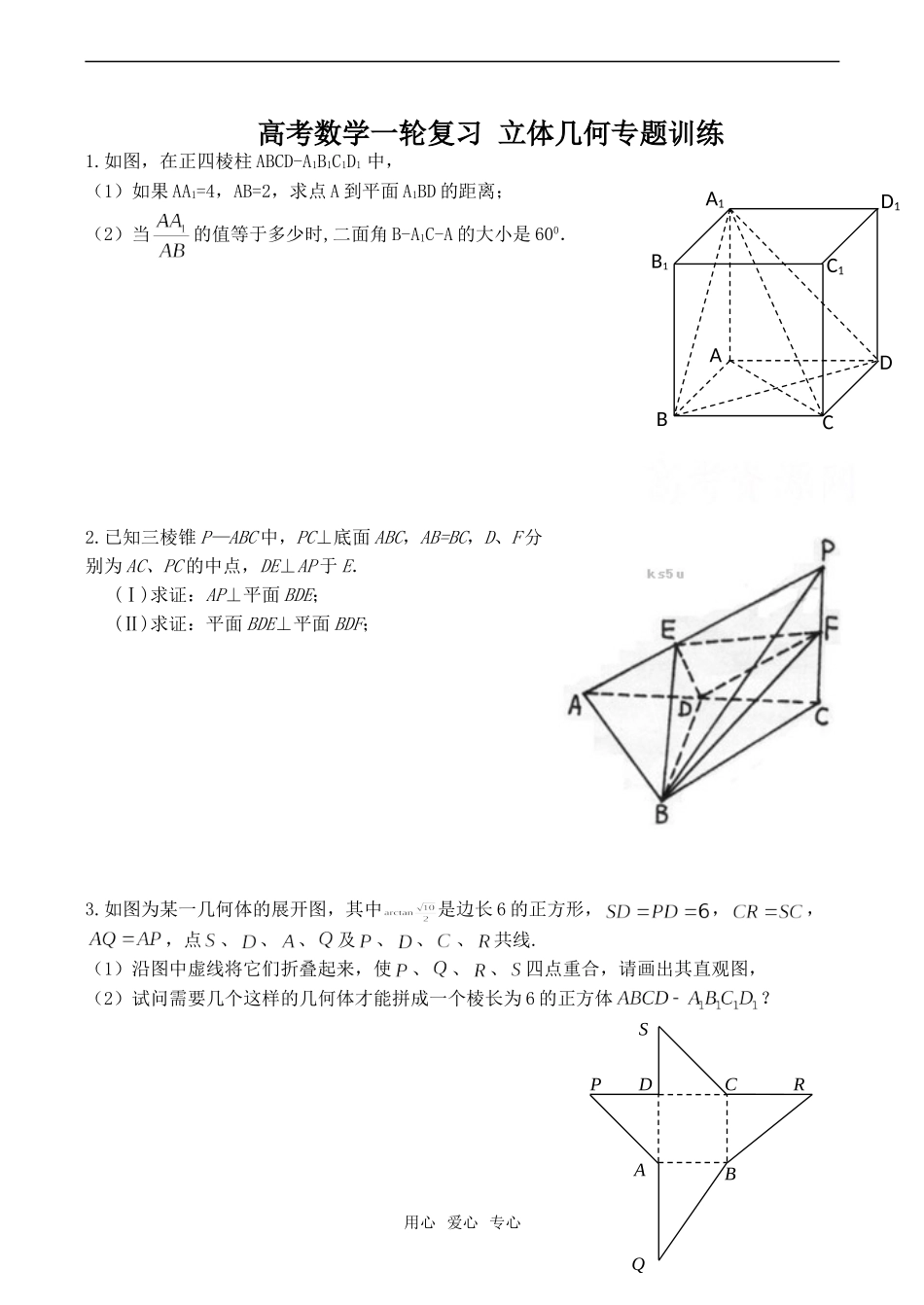
高考数学一轮复习立体几何专题训练1.如图,在正四棱柱ABCD-A1B1C1D1中,w.w.w.k.s.5.u.c.o.m(1)如果AA1=4,AB=2,求点A到平面A1BD的距离;(2)当的值等于多少时,二面角B-A1C-A的大小是600.2.已知三棱锥P—ABC中,PC⊥底面ABC,AB=BC,D、F分别为AC、PC的中点,DE⊥AP于E.(Ⅰ)求证:AP⊥平面BDE;(Ⅱ)求证:平面BDE⊥平面BDF;3.如图为某一几何体的展开图,其中是边长6的正方形,,,,点、、、及、、、共线.(1)沿图中虚线将它们折叠起来,使、、、四点重合,请画出其直观图,(2)试问需要几个这样的几何体才能拼成一个棱长为6的正方体?用心爱心专心B1C1CADD1A1BAQBPDSCR4.已知在侧棱垂直于底面的三棱柱ABC—A1B1C1中AC=3,AB=5,.(Ⅰ)求证:;(Ⅱ)求证:AC1//平面CDB1;(Ⅲ)求三棱锥A1—B1CD的体积.5.如图,在正四棱柱ABCD—A1B1C1D1中,AA1=AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.(Ⅰ)求证:EM∥平面A1B1C1D1;(Ⅱ)求二面角B—A1N—B1的正切值.6.已知四面体ABCD沿AB,AC,AD剪开展成的平面图形正好是下图所示的直角梯形A1A2A3D(梯形中的三点A1,A2,A3重合于四面体中的点A).(1)证明:AB⊥CD;(2)当A1D=10,A1A2=8时,求二面角A—CD—B的平面角;用心爱心专心210arctan(3)在(2)的条件下,求四面体ABCD的体积.7.已知长方体ABCD-中,棱AB=BC=3,=4,连结,过B点作的垂线交于E,交于F奎屯王新敞新疆(1)求证:⊥平面EBD;(2)求ED与平面所成角的大小;(3)求二面角E-BD-C的大小奎屯王新敞新疆8.如图:四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,点F是PB的中点,点E在边BC上移动.(Ⅰ)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;(Ⅱ)证明:无论点E在BC边的何处,都有PE⊥AF;(Ⅲ)当BE等于何值时,PA与平面PDE所成角的大小为45°9.如图,三棱柱ABC—A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.(Ⅰ)求证:AB1//面BDC1;(Ⅱ)求二面角C1—BD—C的余弦值;用心爱心专心EC1B1A1CBA(Ⅲ)在侧棱AA1上是否存在点P,使得CP⊥面BDC1?并证明你的结论.10.如图,在三棱拄中,侧面,已知(1)求证:;(2)试在棱(不包含端点上确定一点的位置,使得;(3)在(2)的条件下,求二面角的平面角的正切值.11.如下图,正三角形ABC边长为2a,CD是AB所在直线上的高,E,F分别是AC和BC边上的中点,现将⊿ABC沿CD翻折成直角二面角A-DC-B(1)试判断翻折后直线AB与面DEF的位置关系,并说明理由。(2)求二面角B-AC-D的大小。(3)求点C到平面DEF的距离。12.如图,在直三棱柱ABC—A1B1C1中,AC=BC=,AA1=1,∠ACB=90°.用心爱心专心DFECBADECBA(Ⅰ)求异面直线A1B与CB1所成角的大小;(Ⅱ)问:在A1B1边上是否存在一点Q,使得平面QBC与平面A1BC所成的角为30°,若存在,请求点Q的位置,若不存在,请说明理由.13.如图,已知四棱锥P—ABCD的侧面PAD与底面ABCD垂直,△PAD是边长为a的正三角形,ABCD为直角梯形,AB//CD,DC=2a,∠ADC=90°,∠DCB=45°,E为BP中点,F在PC上且PF=PC.(Ⅰ)求证EF//平面PAD;(Ⅱ)求三棱锥E—PCD的体积.14.如图,已知直三棱柱ABC—A1B1C1中,AB=AC,D为BC中点,F为BB1上一点,BF=BC=2,FB1=1.(Ⅰ)求证AD⊥平面BB1C1C;(Ⅱ)若E为AD上不同于A、D的任一点,求证:EF⊥FC1;(Ⅲ)若A1B1=3,求FC1与平面AA1B1B所成角的大小.15.如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1.(1)在BC边上是否存在点Q,使得PQ⊥QD,说明理由;(2)若BC边上有且仅有一个点Q,使PQ⊥QD,求AD与平面PDQ所成角的正弦大小;(3)在(2)的条件下,求平面PQD与平面PAB所成角的余弦大小.用心爱心专心A1AB1BC1CPABCDFEABCA1B1C1DFE16.如图,在四棱锥中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=,,.(1)求点D到平面PBC的距离;(2)求二面角的大小.17.如图所示,四棱锥P—ABCD中,侧棱PA与底面ABCD垂直,DC=1,AD=AP=2,AB=5,∠CDA=∠DAB=90°,E是PB的中点.(1)求证:BC⊥平面PAC;(2)求异面直线PD、AE所成角的大小;(3)求二面角A-CE-B的...