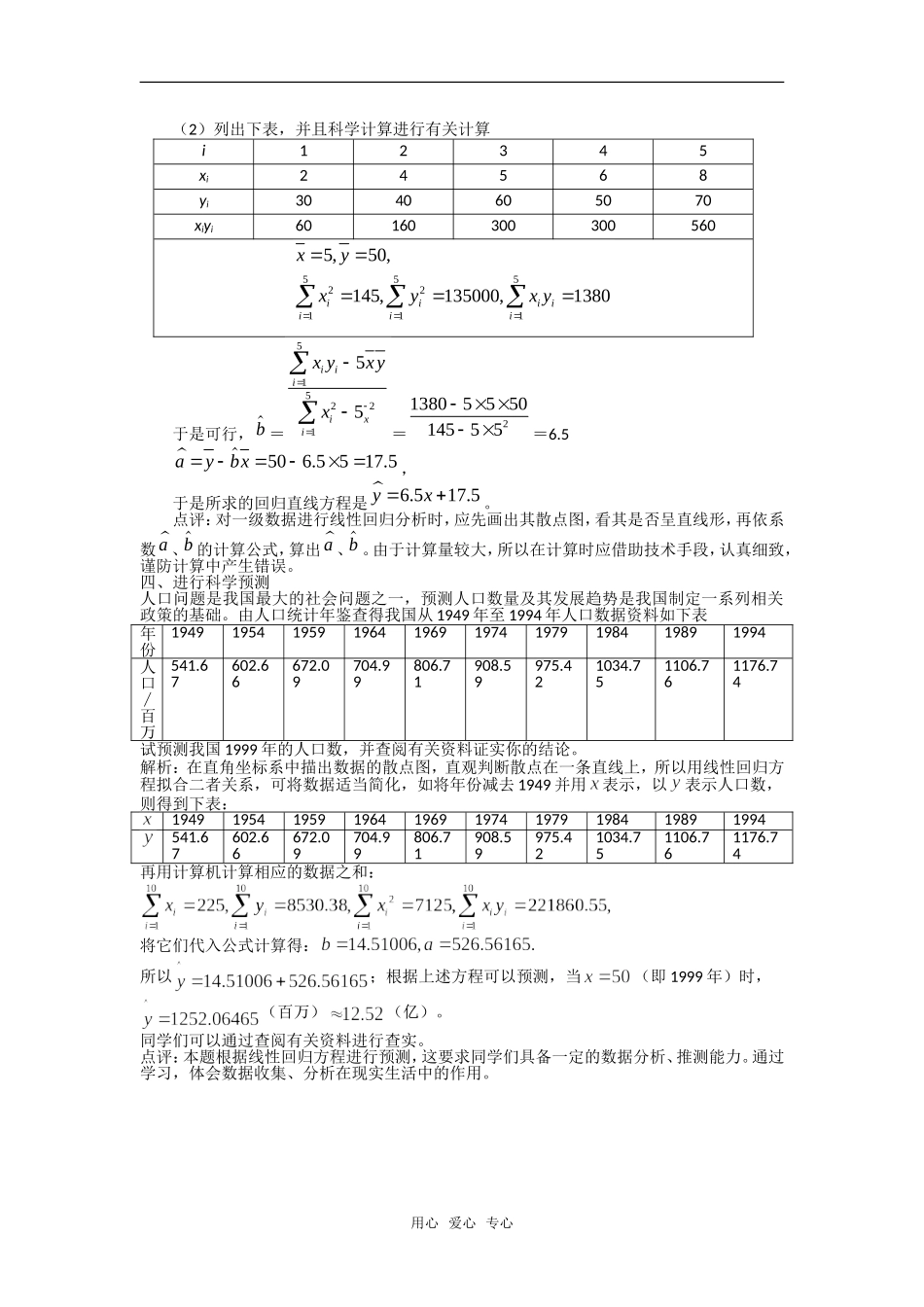
变量相关性的考点分析变量的相关性在2007年高考中开始涉及,预测今后的高考中,利用散点图判断两个变量之间是否具有相关关系,求解回归方程,并进行相应的预测将是考查的重点。下面就其考查的知识点进行分析,以期对同学们有所帮助。一、相关关系的考查例1:下列关系中,是带有随机性相关关系的是。①正方形的边长与面积之间的关系;②水稻产量与施肥量之间的关系;③人的身高与年龄之间的关系;④降雪量与交通事故的发生率之间的关系分析:两变量之间的关系有两种:函数关系与带有随机性的相关关系。①正方形的边长与面积之间的关系是函数关系。②水稻产量与施肥量之间不是严格的函数关系,但是具有相关性,因而是相关关系。③人的身高与年龄之间的关系既不是函数关系,也不是相关关系,因为人的年龄达到一定时期身高就不发生明显变化了,因而他们不具相关关系。④降雪与交通事故的发生率之间具有相关关系。答案:②④点评:准确理解变量间的相关关系是解答本题的关键。二、散点图的考查例2:现随机抽取某校10名学生在入学考试中的数学成绩x与入学后的第一次数学成绩y,数据如下:学号12345678910X12010811710410311010410599108Y84648468696869465771问这10名学生的两次数学考试成绩是否具有相关关系?解::应用散点图分析:两次数学考试成绩散点图如图所示,由散点图可以看出两个变量的对应点集中在一条直线的周围,且y随x的变大而变大,具有正相关关系。因此,这10名学生的两次数学考试成绩具有相关关系。点评:两个变量是否具有相关关系,主要依据散点图加以判断,看变量对应的点是否分布在一条直线附近,或是,则具有相关关系,否则,不具有相关关系。三、求线性回归直线方程例3:某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:x24568y3040605070(1)画出散点图;(2)求回归直线方程。解:(1)散点图如图用心爱心专心(2)列出下表,并且科学计算进行有关计算i12345xi24568yi3040605070xiyi60160300300560555221115,50,145,135000,1380iiiiiiixyxyxy于是可行,b=51522155iiiixixyxyx=21380555014555=6.5506.5517.5aybx,于是所求的回归直线方程是6.517.5yx。点评:对一级数据进行线性回归分析时,应先画出其散点图,看其是否呈直线形,再依系数a、b的计算公式,算出a、b。由于计算量较大,所以在计算时应借助技术手段,认真细致,谨防计算中产生错误。四、进行科学预测人口问题是我国最大的社会问题之一,预测人口数量及其发展趋势是我国制定一系列相关政策的基础。由人口统计年鉴查得我国从1949年至1994年人口数据资料如下表年份1949195419591964196919741979198419891994人口∕百万541.67602.66672.09704.99806.71908.59975.421034.751106.761176.74试预测我国1999年的人口数,并查阅有关资料证实你的结论。解析:在直角坐标系中描出数据的散点图,直观判断散点在一条直线上,所以用线性回归方程拟合二者关系,可将数据适当简化,如将年份减去1949并用表示,以表示人口数,则得到下表:1949195419591964196919741979198419891994541.67602.66672.09704.99806.71908.59975.421034.751106.761176.74再用计算机计算相应的数据之和:将它们代入公式计算得:所以;根据上述方程可以预测,当(即1999年)时,(百万)(亿)。同学们可以通过查阅有关资料进行查实。点评:本题根据线性回归方程进行预测,这要求同学们具备一定的数据分析、推测能力。通过学习,体会数据收集、分析在现实生活中的作用。用心爱心专心