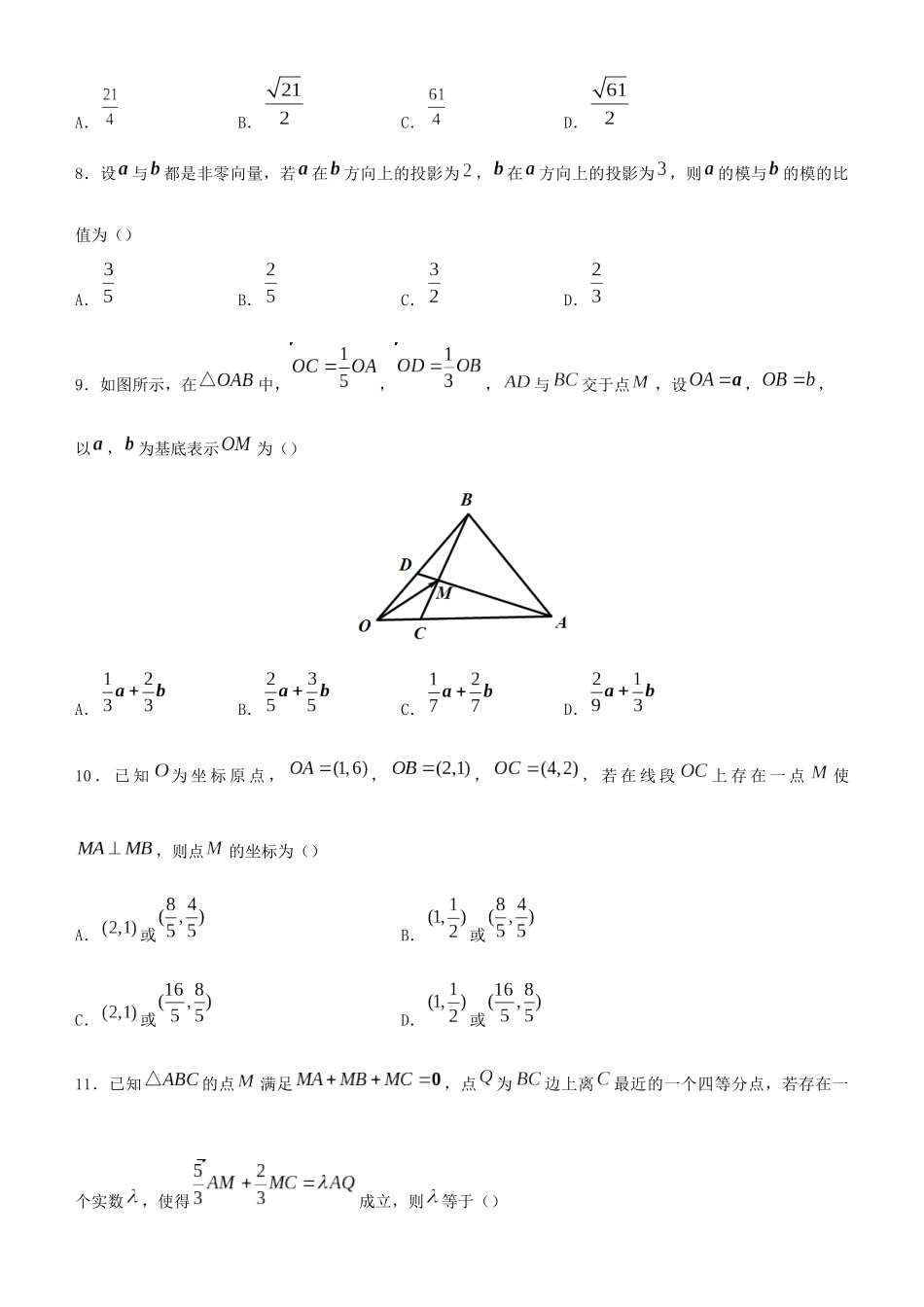
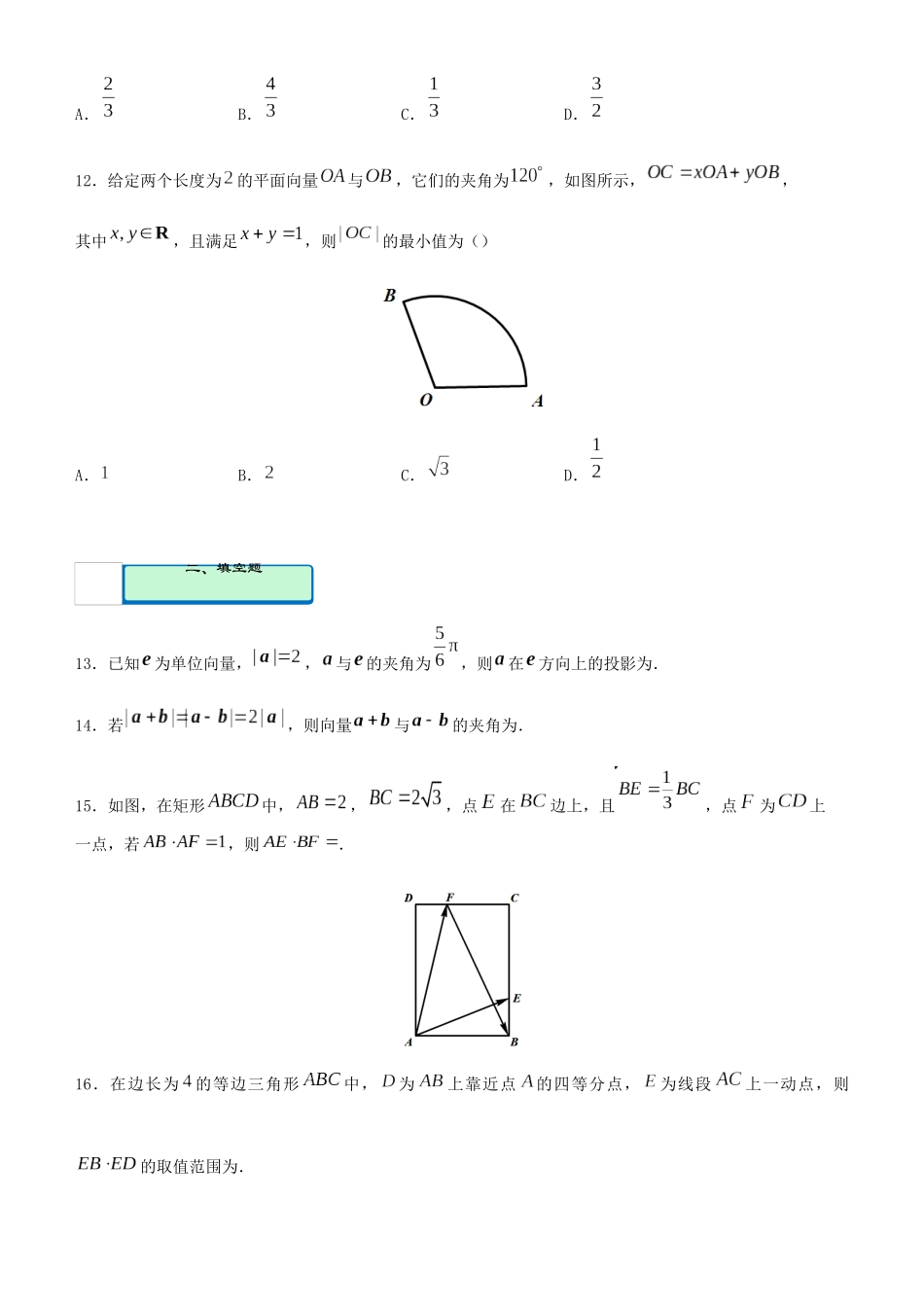
一、选择题疯狂专练19平面向量1.下列说法正确的是()A.与是相等向量B.零向量与任何向量都是共线向量C.平行向量是共线向量D.共线的单位向量都相等2.已知平面向量,,则向量()A.B.C.D.3.设,,若,则实数的值为()A.B.C.D.4.设,,分别为的三边,,的中点,则()A.B.C.D.5.已知点,,则与向量同方向的单位向量为()A.B.C.D.6.已知平面向量,,且,则()A.B.C.D.7.已知向量,夹角为,且,,则()A.B.C.D.8.设与都是非零向量,若在方向上的投影为,在方向上的投影为,则的模与的模的比值为()A.B.C.D.9.如图所示,在中,,,与交于点,设,,以,为基底表示为()A.B.C.D.10.已知为坐标原点,,,,若在线段上存在一点使,则点的坐标为()A.或B.或C.或D.或11.已知的点满足,点为边上离最近的一个四等分点,若存在一个实数,使得成立,则等于()二、填空题A.B.C.D.12.给定两个长度为的平面向量与,它们的夹角为,如图所示,,其中,且满足,则的最小值为()A.B.C.D.13.已知为单位向量,,与的夹角为,则在方向上的投影为.14.若,则向量与的夹角为.15.如图,在矩形中,,,点在边上,且,点为上一点,若,则.16.在边长为的等边三角形中,为上靠近点的四等分点,为线段上一动点,则的取值范围为.答案与解析一、选择题1.【答案】C【解析】与是相反向量,故A错误;零向量与任何向量共线,但不是共线向量,故B错误;平行向量也称为共线向量,故C正确;共线的单位向量模长相等,方向相同或相反,方向相同时为相等向量,方向相反时为相反向量,故D错误.2.【答案】B【解析】,,∴,故选B.3.【答案】A【解析】,∵,∴,则有,解得,故选A.4.【答案】D【解析】∵,,分别为的三边,,的中点,∴.5.【答案】A【解析】由题意可得,选项B与方向相反,选项,均不与共线,故选A.6.【答案】B【解析】∵,∴,得,∴,,,∴.7.【答案】D【解析】依题可得,∴,故选D.8.【答案】D【解析】由题意可知,,,则.9.【答案】C【解析】设,则,.∵,,三点共线,∴,即①;而,,∵,,三点共线,∴,即②;联立①②解得,∴.10.【答案】C【解析】设存在点,且,,,∵,∴,∴,即,,解得或.当时,,点的坐标为;当时,,点的坐标为.故点的坐标为或.11.【答案】B【解析】∵,可知为中线交点,延长交于,则为中点,∵为边上离最近的一个四等分点,∴为中点,∵成立,,二、填空题∴.12.【答案】A【解析】如下图所示,以为平面直角坐标原点,方向为的正方向,与垂直方向轴,建立平面直角坐标系,则,,.∵,∴,,当时,有最小值为,∴的最小值为.13.【答案】【解析】依题意有在方向上的投影为.14.【答案】【解析】∵,∴,∴,∵,得,设向量与的夹角为,∴,∴.15.【答案】【解析】由题意可得,∴,∴,得,∴,又∵,,∴,∴.16.【答案】【解析】由题意得,与的夹角为,设,∴,由于为线段上一动点,∴.令,∴当时,,当时,,∴的取值范围为.