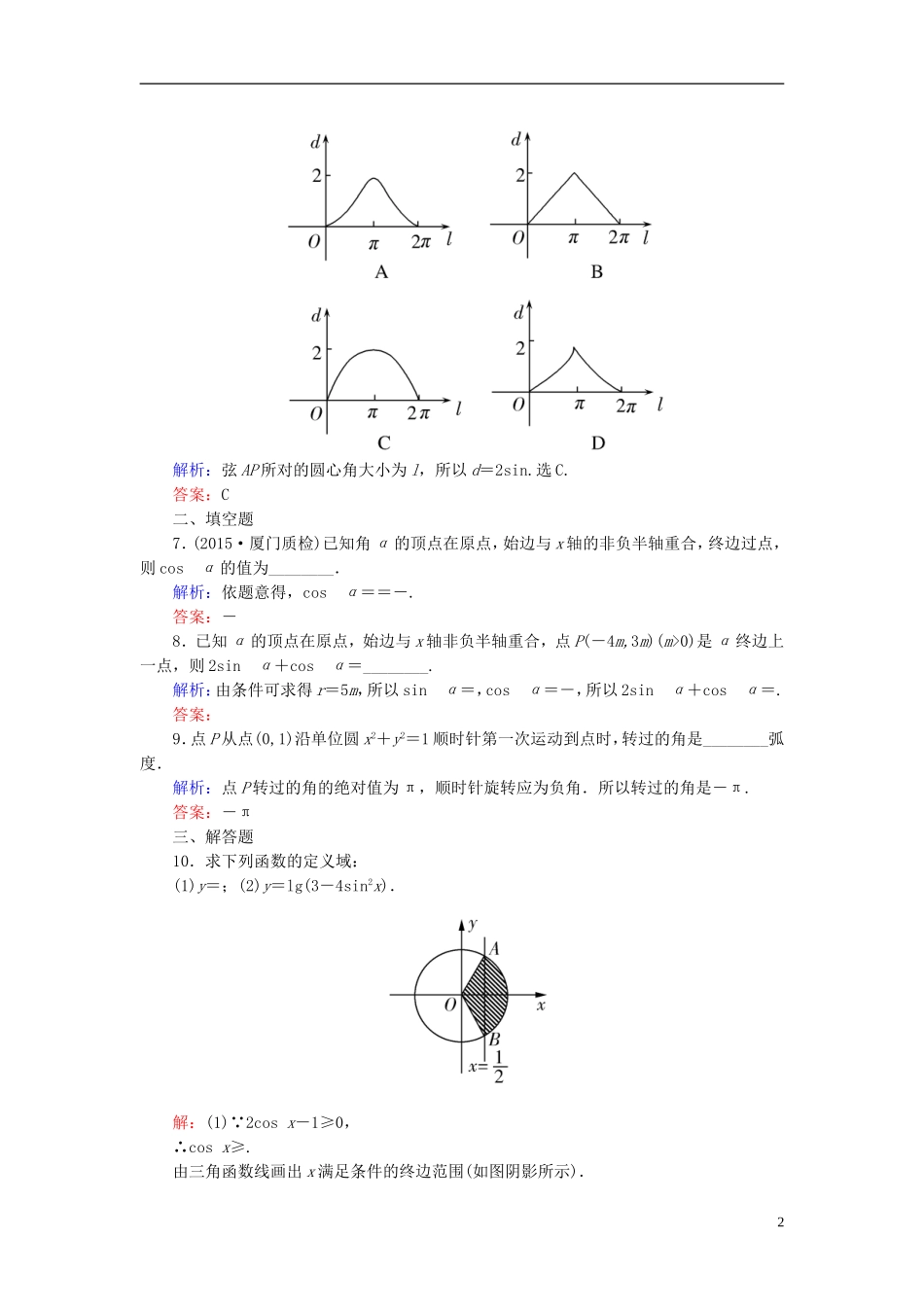
【与名师对话】2016版高考数学一轮复习3.1任意角和弧度制及任意角的三角函数课时跟踪训练文一、选择题1.若α=k·180°+45°(k∈Z),则α在()A.第一或第三象限B.第一或第二象限C.第二或第四象限D.第三或第四象限解析:当k=2m+1(m∈Z)时,α=2m·180°+225°=m·360°+225°,故α为第三象限角;当k=2m(m∈Z)时,α=m·360°+45°,故α为第一象限角.答案:A2.若角α和角β的终边关于x轴对称,则角α可以用角β表示为()A.2kπ+β(k∈Z)B.2kπ-β(k∈Z)C.kπ+β(k∈Z)D.kπ-β(k∈Z)解析:因为角α和角β的终边关于x轴对称,所以α+β=2kπ(k∈Z).所以α=2kπ-β(k∈Z).答案:B3.若-<α<0,则点P(tanα,cosα)位于()A.第一象限B.第二象限C.第三象限D.第四象限解析:∵-<α<0,∴tanα<0,cosα>0,∴点P在第二象限.答案:B4.(2014·北京东城模拟)点P从(1,0)出发,沿单位圆x2+y2=1逆时针方向运动弧长到达Q点,则Q点的坐标为()A.B.C.D.解析:设α=∠POQ,由三角函数定义可知,Q点的坐标(x,y)满足x=cosα,y=sinα,∴x=-,y=,∴Q点的坐标为.答案:A5.已知点P落在角θ的终边上,且θ∈[0,2π),则θ的值为()A.B.C.D.解析:由sin>0,cos<0知角θ是第四象限的角,∵tanθ==-1,θ∈[0,2π),∴θ=.答案:D6.如图,设点A是单位圆上的一定点,动点P从A出发在圆上按逆时针方向转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图象大致为()1解析:弦AP所对的圆心角大小为l,所以d=2sin.选C.答案:C二、填空题7.(2015·厦门质检)已知角α的顶点在原点,始边与x轴的非负半轴重合,终边过点,则cosα的值为________.解析:依题意得,cosα==-.答案:-8.已知α的顶点在原点,始边与x轴非负半轴重合,点P(-4m,3m)(m>0)是α终边上一点,则2sinα+cosα=________.解析:由条件可求得r=5m,所以sinα=,cosα=-,所以2sinα+cosα=.答案:9.点P从点(0,1)沿单位圆x2+y2=1顺时针第一次运动到点时,转过的角是________弧度.解析:点P转过的角的绝对值为π,顺时针旋转应为负角.所以转过的角是-π.答案:-π三、解答题10.求下列函数的定义域:(1)y=;(2)y=lg(3-4sin2x).解:(1)∵2cosx-1≥0,∴cosx≥.由三角函数线画出x满足条件的终边范围(如图阴影所示).2∴x∈(k∈Z).(2)∵3-4sin2x>0,∴sin2x<,∴-0时,r=t,sinα===,cosα===,tanα===2;当t<0时,r=-t,sinα===-,cosα===-,tanα===2.综上可知,sinα=,cosα=,tanα=2或sinα=-,cosα=-,tanα=2.3