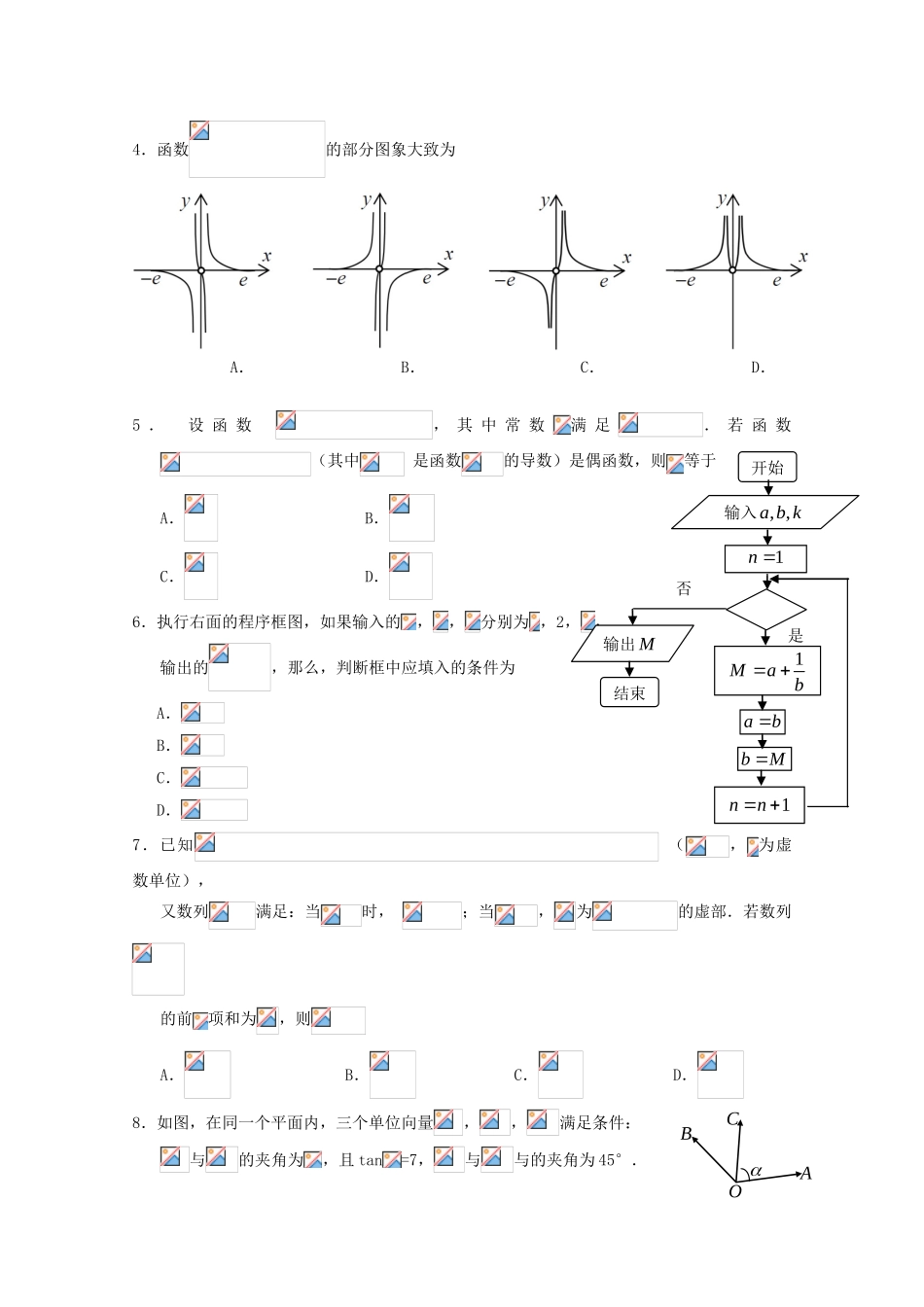
广东省六校2018届高三数学下学期第三次联考试题理满分:150分考试时间:120分钟注意事项:1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上.用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码横贴在答题卡右上角“条形码粘贴处”.2.作答选择题时,选出每小题答案后,用2B铅笔在答题卡上对应题目选项的答案信息点涂黑;如需要改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液.不按以上要求作答无效.4.考生必须保证答题卡的整洁.考试结束后,将试卷和答题卡一并交回.一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合为实数,且,为实数,且,则的元素个数为A.0B.1C.2D.32.设等差数列的前项和为,若,,则A.B.C.D.3.若变量满足约束条件,则的取值范围是A.B.C.D.4.函数的部分图象大致为A.B.C.D.5.设函数,其中常数满足.若函数(其中是函数的导数)是偶函数,则等于A.B.C.D.6.执行右面的程序框图,如果输入的,,分别为,2,,输出的,那么,判断框中应填入的条件为A.B.C.D.7.已知(,为虚数单位),又数列满足:当时,;当,为的虚部.若数列的前项和为,则A.B.C.D.8.如图,在同一个平面内,三个单位向量,,满足条件:与的夹角为,且tan=7,与与的夹角为45°.否1n输入,,abk输出M开始是1Mabab结束1nnbMAOCB若(),则的值为A.B.C.D.9.四面体中,三组对棱的长分别相等,依次为5,4,,则的取值范围是A.B.C.D.10.从2个不同的红球、2个不同的黄球、2个不同的蓝球共六个球中任取2个,放入红、黄、蓝色的三个袋子中,每个袋子至多放入一个球,且球色与袋色不同,那么不同的放法有A.种B.种C.种D.种11.已知点为双曲线的右焦点,直线与交于,两点,若,设,且,则该双曲线的离心率的取值范围是A.B.C.D.12.已知是函数与图象的两个不同的交点,则的取值范围是A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分.13.已知函数是定义在上的奇函数,则__________.14.已知函数,若,则函数恒过定点_____.15.已知几何体的三视图如图所示,其中俯视图为一正方形,则该几何体的表面积为.16.若函数的图象上存在不同的两点,,其中使得的最大值为0,则称函数是“柯西函数”.给出下列函数:①;②;③;④.其中是“柯西函数”的为(填上所有正确答案的序号)三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第1721题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)设数列的前项和为,数列的前项和为,满足.(Ⅰ)求的值;(Ⅱ)求数列的通项公式.18.(12分)某小店每天以每份5元的价格从食品厂购进若干份食品,然后以每份10元的价格出售.如果当天卖不完,剩下的食品还可以每份1元的价格退回食品厂处理.(Ⅰ)若小店一天购进16份,求当天的利润(单位:元)关于当天需求量(单位:份,)的函数解析式;(Ⅱ)小店记录了100天这种食品的日需求量(单位:份),整理得下表:日需求量14151617181920频数10201616151310以100天记录的各需求量的频率作为各需求量发生的概率.(i)小店一天购进16份这种食品,表示当天的利润(单位:元),求的分布列及数学期望;(ii)以小店当天利润的期望值为决策依据,你认为一天应购进食品16份还是17份?19.(12分)如图,在四棱锥中,是平行四边形,,,,,,分别是,的中点.(Ⅰ)证明:平面平面;(Ⅱ)求二面角的余弦值.20.(12分)已知椭圆的离心率为,、分别为椭圆的左、右顶点,点满足.(Ⅰ)求椭圆的方程;(Ⅱ)设直线经过点且与交于不同的两点、,试问:在轴上是否存在点,使得直线与直线的斜率的和为定值?若存在,请求出点的坐标及定值;若不存在,请说明理由.21.(12分)已知函数,其中.(Ⅰ)函...