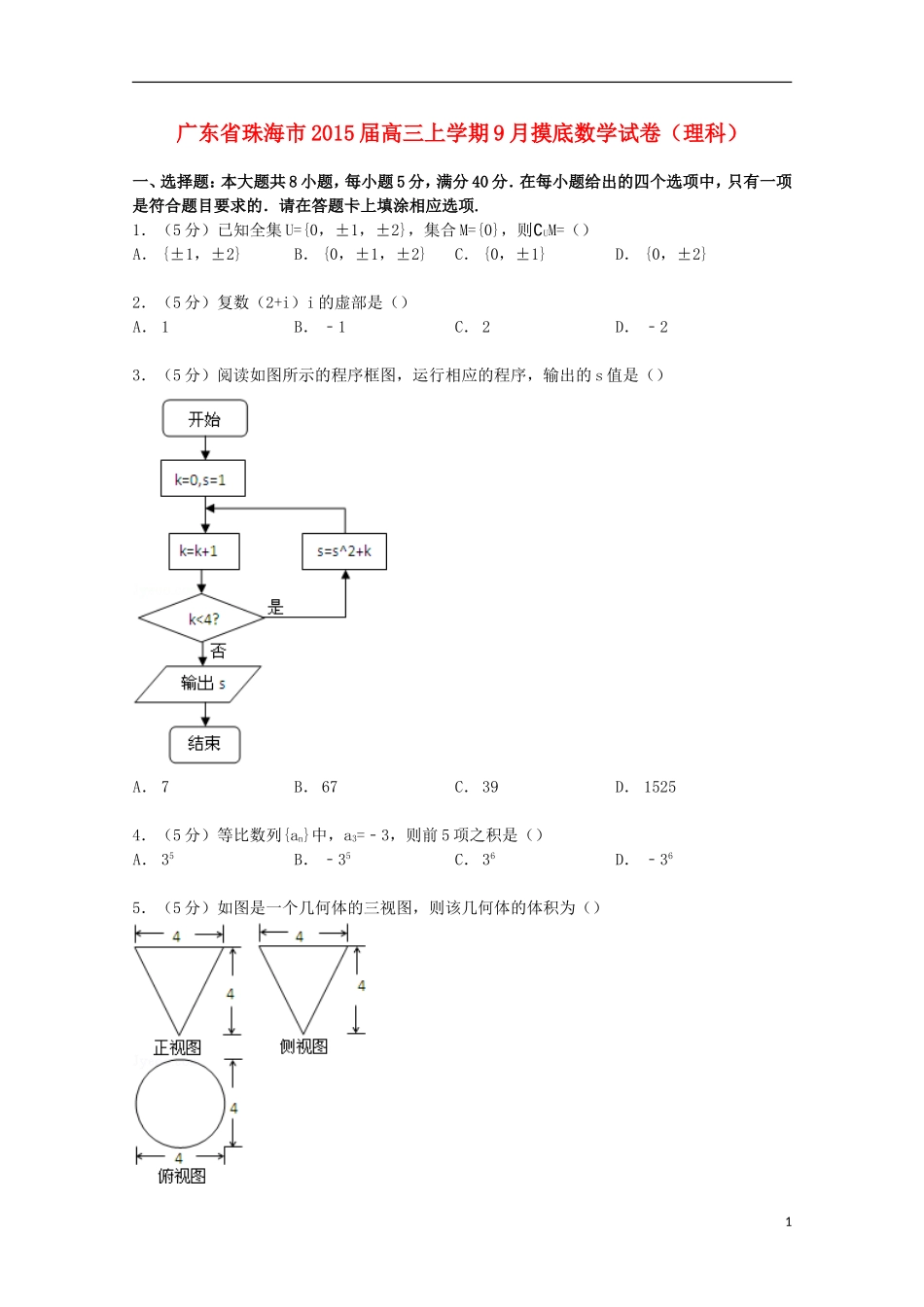
广东省珠海市2015届高三上学期9月摸底数学试卷(理科)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项.1.(5分)已知全集U={0,±1,±2},集合M={0},则∁UM=()A.{±1,±2}B.{0,±1,±2}C.{0,±1}D.{0,±2}2.(5分)复数(2+i)i的虚部是()A.1B.﹣1C.2D.﹣23.(5分)阅读如图所示的程序框图,运行相应的程序,输出的s值是()A.7B.67C.39D.15254.(5分)等比数列{an}中,a3=﹣3,则前5项之积是()A.35B.﹣35C.36D.﹣365.(5分)如图是一个几何体的三视图,则该几何体的体积为()1A.B.16πC.D.8π6.(5分)向量=(0,1,﹣1),=(0,1,0),则与的夹角为()A.0°B.30°C.45°D.60°7.(5分)在区间[0,2]上随机取两个数x,y其中满足y≥2x的概率是()A.B.C.D.8.(5分)下列命题中是真命题的是()A.∀α、β∈R,均有cos(α+β)=cosα﹣cosβB.若f(x)=cos(2x﹣φ)为奇函数,则φ=kπ,k∈ZC.命题“p”为真命题,命题“q”为假命题,则命题“¬p∨q”为假命题D.x=0是函数f(x)=x3﹣2的极值点二、填空题:本大题共5小题,每小题5分,考生作答6小题,满分25分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.请将答案填在答题卡相应位置.9.(5分)不等式|3x﹣4|≤4的解集是.10.(5分)的展开式中x3的系数为10,则实数a=.11.(5分)=.12.(5分)已知变量x,y满足约束条件,则目标函数z=x+y的最大值为.13.(5分)在平面直角坐标系xOy中,曲线C:x2=﹣2py(p>0)的焦点F,点M(p,yM)∈C,若M为圆心的圆与曲线C的准线相切,圆面积为36π,则p=.(几何证明选讲选做题)14.(5分)如图,在Rt△ABC中,斜边AB=12,直角边AC=6,如果以C为圆心的圆与AB相切于D,则⊙C的半径长为.2(极坐标选做题)15.以直角坐标系的原点为极点,x轴非负半轴为极轴,建立极坐标系,在两种坐标系中取相同的单位长度,点A的极坐标为(2,),曲线C的参数方程为,则曲线C上的点B与点A距离的最大值为.三、解答题:本题共有6个小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(12分)已知函数f(x)=2sinx•cosx+2cos2x,x∈R.(1)求f(x)的最小正周期;(2)已知f()=,α∈[0,π],求cos(α+)的值.17.(12分)某校兴趣小组进行了一项“娱乐与年龄关系”的调查,对15~65岁的人群随机抽取1000人的样本,进行了一次“是否是电影明星追星族”调查,得到如下各年龄段样本人数频率分布直方图和“追星族”统计表:“追星族”统计表组数分组“追星族”人数占本组频率一[15,25)a0.75二[25,35)2000.40三[35,45)50.1四[45,55)3b五[55,65]20.1(1)求a,b的值.(2)设从45岁到65岁的人群中,随机抽取2人,用样本数据估计总体,ξ表示其中“追星族”的人数,求ξ分布列、期望和方差.318.(14分)如图,长方体ABCD﹣A1B1C1D1中,E、F、G分别为AB、C1D1、DC中点,AB=2,AD=,AC1=3(1)求证:C1E∥平面AFC.(2)求二面角F﹣AC﹣G的正切值.19.(14分)已知数列{an},an≠2,an+1=,a1=3.(1)证明:数列{}是等差数列.(2)设bn=an﹣2,数列{bnbn+1}的前n项和为Sn,求使(2n+1)•2n+2•Sn>(2n﹣3)•2n+1+192成立的最小正整数n.20.(14分)焦点在x轴的椭圆C1:+=1(3≤a≤4),过C1右顶点A2(a,0)的直线l:y=k(x﹣a)(k>0)与曲线C2:y=x2﹣相切,交C1于A2、E二点.(1)若C1的离心率为,求C1的方程.4(2)求|A2E|取得最小值时C2的方程.21.(14分)已知函数f(x)=(1)若函数f(x)在(a﹣1,a+1)(a>1)上有极值点,求实数a的范围.(2)求证:x≥1时,x(x+1)f(x)>.广东省珠海市2015届高三上学期9月摸底数学试卷(理科)参考答案与试题解析一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项.1.(5分)已知全集U={0,±1,±2},集合M={0},则∁UM=()A.{±1,±2}B.{0,±1,±2}...