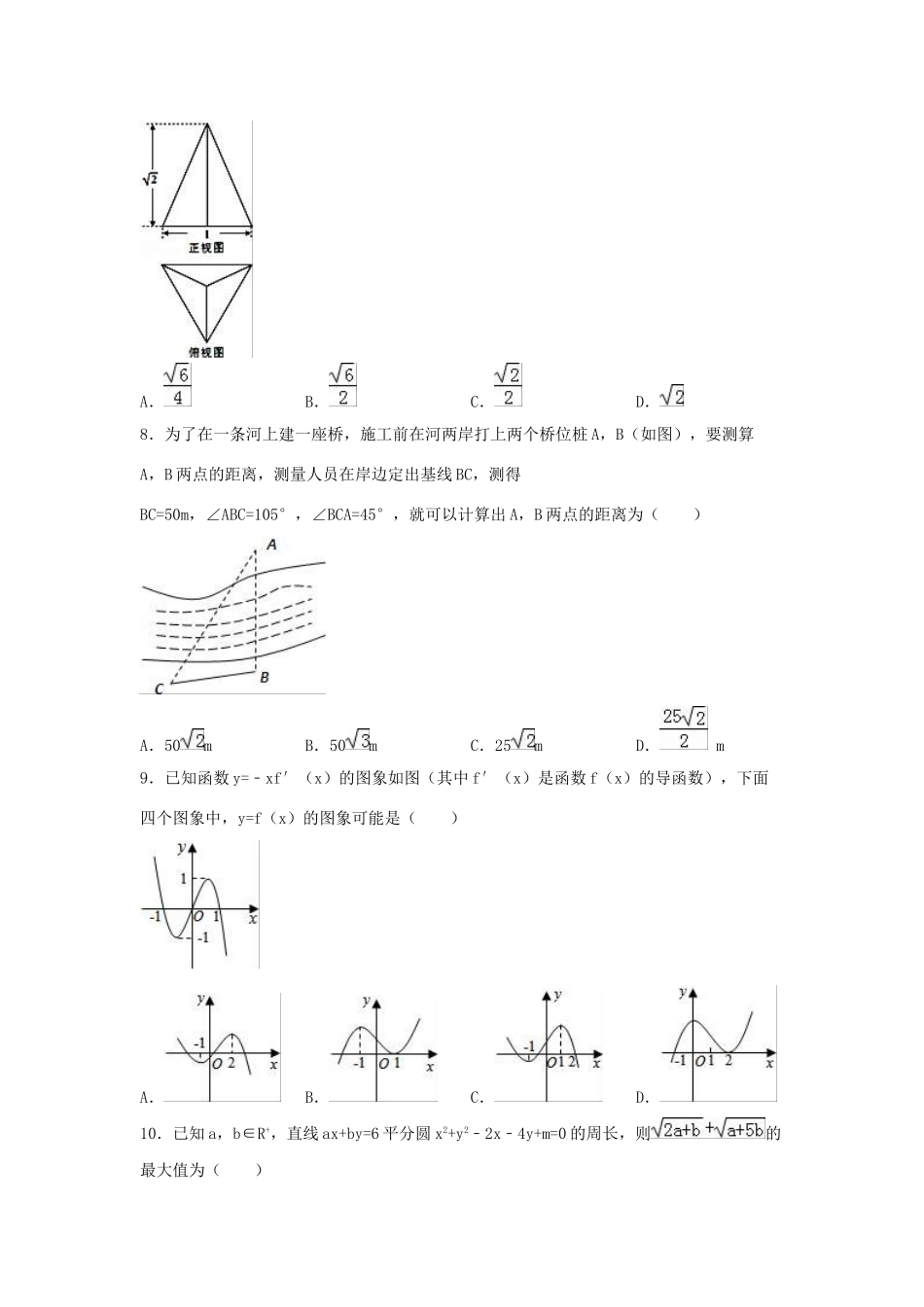
2014-2015学年河南省漯河高中高三(上)周测数学试卷(文科)(12.25)一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集U={x∈N+|x<6},集合A={1,3},B={3,5},则∁U(A∪B)=()A.{1,4}B.{1,5}C.{2,4}D.{2,5}2.已知复数z1=3﹣bi,z2=1﹣2i,若是实数,则实数b的值为()A.6B.﹣6C.0D.3.A.||=||||B.()2=C.若⊥(﹣)则=D.若=则=4.已知sinαcosα=,且<α<,则cosα﹣sinα的值为()A.B.C.D.5.已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2等于()A.﹣10B.﹣8C.﹣6D.﹣46.下列判断正确的是()A.“正四棱锥的底面是正方形”的逆命题为真命题.B.“ac2>bc2”的充要条件是“a>b”.C.不等式>1的解集为{x|x<2}.D.若“p或q”是真命题,则p,q中至少有一个真命题.7.已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为()A.B.C.D.8.为了在一条河上建一座桥,施工前在河两岸打上两个桥位桩A,B(如图),要测算A,B两点的距离,测量人员在岸边定出基线BC,测得BC=50m,∠ABC=105°,∠BCA=45°,就可以计算出A,B两点的距离为()A.50mB.50mC.25mD.m9.已知函数y=﹣xf′(x)的图象如图(其中f′(x)是函数f(x)的导函数),下面四个图象中,y=f(x)的图象可能是()A.B.C.D.10.已知a,b∈R+,直线ax+by=6平分圆x2+y2﹣2x﹣4y+m=0的周长,则的最大值为()A.6B.4C.3D.11.已知函数f(x)=满足对任意的实数x1≠x2都有<0成立,则实数a的取值范围为()A.(﹣∞,2)B.(﹣∞,]C.(﹣∞,2]D.[,2)12.(5分)(2014赤峰模拟)若函数y=f(x)图象上的任意一点P的坐标(x,y)满足条件|x|≥|y|,则称函数f(x)具有性质S,那么下列函数中具有性质S的是()A.f(x)=ex﹣1B.f(x)=ln(x+1)C.f(x)=sinxD.f(x)=tanx二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)(2016春宜春校级月考)设变量x,y满足约束条件:,则目标函数z=的最小值为.14.(5分)(2014秋东湖区校级期中)已知函数的图象与直线y=m有且只有两个交点,且交点的横坐标分别为x1,x2(x1<x2),那么x1+x2=.15.(5分)(2014郑州一模)已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若AB=AA1=2,AC=1,∠BAC=60°,则此球的表面积等于.16.(5分)(2014长春一模)定义[x]表示不超过x的最大整数,例如:[1.5]=1,[﹣1.5]=﹣2,若f(x)=sin(x﹣[x]),则下列结论中:正确的序号为①y=f(x)是奇函数;②y=f(x)是周期函数,周期为2π;③y=f(x)的最小值为0,无最大值;④y=f(x)无最小值,最大值为sin1.三、解答题:本大题共6小题,共计70分.解答应写出文字说明.证明过程或演算步骤17.(10分)(2009西城区一模)设等差数列{an}的前n项和为Sn,且(c是常数,n∈N*),a2=6.(Ⅰ)求c的值及数列{an}的通项公式;(Ⅱ)证明:.18.(12分)(2015漳州模拟)在四棱锥P﹣ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.(1)若F为PC的中点,求证:PC⊥平面AEF;(2)求四棱锥P﹣ABCD的体积V.19.(12分)(2014秋濠江区校级期末)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.(Ⅰ)求函数f(x)的解析式;(Ⅱ)若,求cosα的值.20.(12分)(2015春微山县校级月考)如图所示,在直三棱柱ABC﹣A1B1C1中,AC⊥BC.(1)求证:平面AB1C1⊥平面AC1;(2)若AB1⊥A1C,求线段AC与AA1长度之比;(3)若D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,试确定点E的位置;若不存在,请说明理由.21.(12分)(2009江苏一模)已知圆x2+y2+2ax﹣2ay+2a2﹣4a=0(0<a≤4)的圆心为C,直线l:y=x+m.(1)若m=4,求直线l被圆C所截得弦长的最大值;(2)若直线l是圆心下方的切线,当a在(0,4]变化时,求m的取值范围.22.(12分)(2015甘肃二模)设函数f(x)=ax﹣lnx,g(x)=ex﹣ax,其中a...