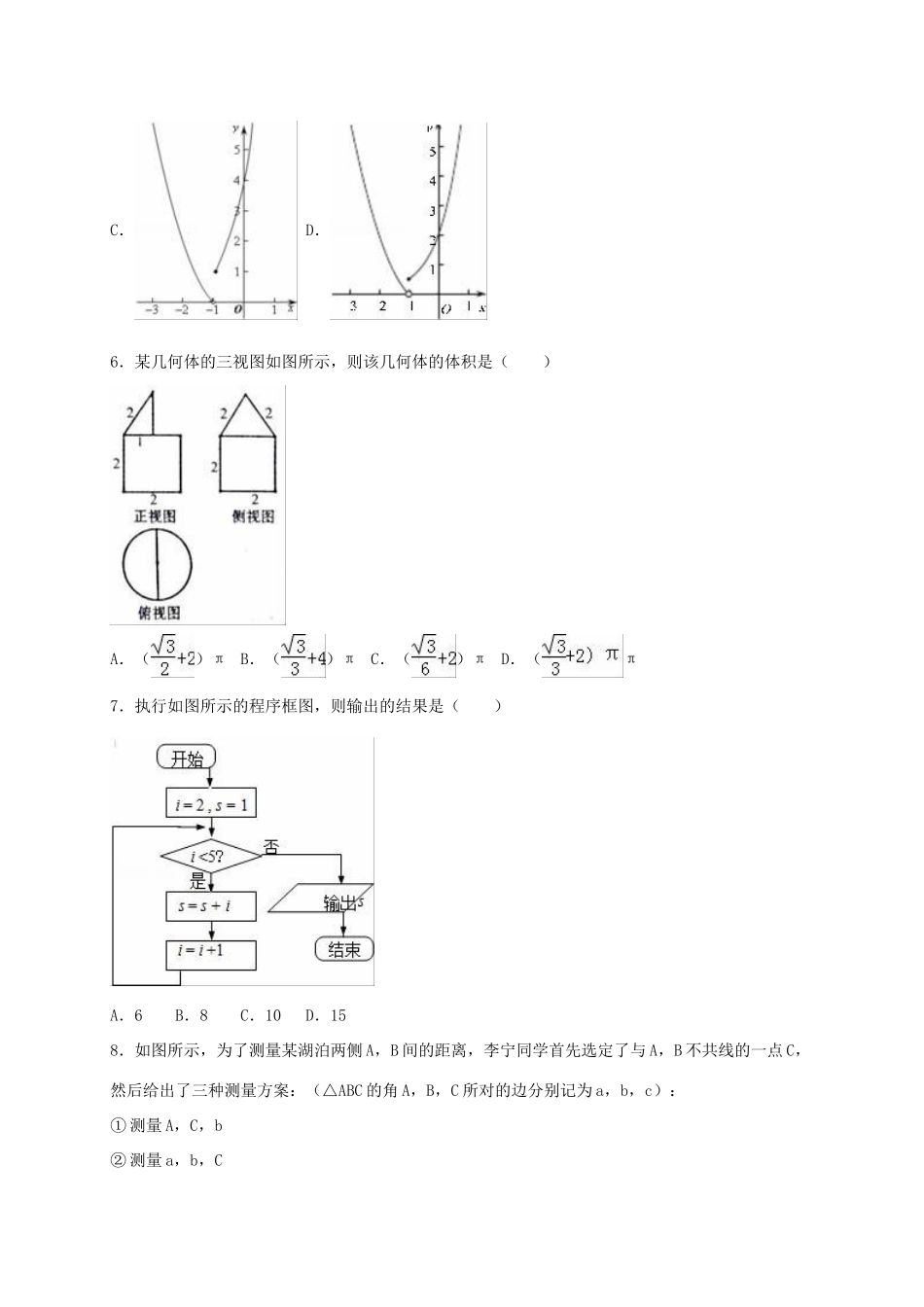
2016年海南省三亚四中高考数学模拟试卷(文科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={x||x|≤1},集合B=Z,则A∩B=()A.{0}B.{x|﹣1≤x≤1}C.{﹣1,0,1}D.∅2.设i是虚数单位,复数在复平面上所表示的点为()A.第一象限B.第二象限C.第三象限D.第四象限3.已知向量,,条件p:,条件q:m=2,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要4.函数f(x)=cos2x+sinxcosx的一个对称中心是()A.(,0)B.(,0)C.(﹣,0)D.(﹣,0)5.定义运算“*”为:a*b=,若函数f(x)=(x+1)*x,则该函数的图象大致是()A.B.C.D.6.某几何体的三视图如图所示,则该几何体的体积是()A.()πB.()πC.()πD.(π7.执行如图所示的程序框图,则输出的结果是()A.6B.8C.10D.158.如图所示,为了测量某湖泊两侧A,B间的距离,李宁同学首先选定了与A,B不共线的一点C,然后给出了三种测量方案:(△ABC的角A,B,C所对的边分别记为a,b,c):①测量A,C,b②测量a,b,C③测量A,B,a则一定能确定A,B间距离的所有方案的个数为()A.3B.2C.1D.09.已知a>0,x,y满足约束条件,若z=2x+y的最小值为,则a=()A.B.C.1D.210.已知点An(n,an)(n∈N*)都在函数f(x)=logax(a>0且a≠1)的图象上,则a2+a10与2a6的大小关系为()A.a2+a10>2a6B.a2+a10<2a6C.a2+a10=2a6D.a2+a10与2a6的大小与a有关11.若函数f(x)=2x3﹣3mx2+6x在区间(2,+∞)上为增函数,则实数m的取值范围是()A.(﹣∞,2)B.(﹣∞,2]C.(﹣∞,)D.(﹣∞,]12.P为双曲线﹣=1的右支上一点,M,N分别是(x+5)2+y2=4圆和(x﹣5)2+y2=1上的点,则|PM|﹣|PN|的最大值为()A.8B.9C.10D.7二、填空题:本大题共4小题,每小题5分.13.高三某学习小组对两个相关变量收集到6组数据如下表:x102030405060y3928mn4341由最小二乘法得到回归直线方程=0.82x+11.3,发现表中有两个数据模糊不清,则这两个数据的和是.14.直三棱柱ABC﹣A1B1C1的顶点在同一个球面上,AB=3,AC=4,AA1=2,∠BAC=90°,则球的表面积.15.设抛物线x2=4y的焦点为F,经过点P(1,4)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,则||+||=.16.观察下列等式:(1+1)=2×1(2+1)(2+2)=22×1×3(3+1)(3+2)(3+3)=23×1×3×5…照此规律,第n个等式可为.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知等差数列{an}中,a1=﹣2,公差d=3;数列{bn}中,Sn为其前n项和,满足(n∈N+).(1)记,求数列{cn}的前n项和Tn;(2)求证:数列{bn}是等比数列.18.解放军某部在实兵演练对抗比赛中,红、蓝两个小组均派6人参加实弹射击,其所得成绩的茎叶图如图所示.(1)根据射击数据,计算红、蓝两个小组射击成绩的均值与方差,并说明红军还是蓝军的成绩相对比较稳定;(2)若从蓝军6名士兵中随机抽取两人,求所抽取的两人的成绩之差不超过2的概率.19.如图,四棱锥P﹣ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA上的动点.(1)求四棱锥P﹣ABCD的体积;(2)如果E是PA的中点,求证:PC∥平面BDE;(3)是否不论点E在侧棱PA的任何位置,都有BD⊥CE?证明你的结论.20.在平面直角坐标系xOy中,以动圆经过点(1,0)且与直线x=﹣1相切,若该动圆圆心的轨迹为曲线E.(1)求曲线E的方程;(2)已知点A(5,0),倾斜角为的直线l与线段OA相交(不经过点O或点A)且与曲线E交于M、N两点,求△AMN面积的最大值,及此时直线l的方程.21.已知函数f(x)=x2+2alnx.(Ⅰ)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;(Ⅱ)求函数f(x)的单调区间;(Ⅲ)若函数在[1,2]上是减函数,求实数a的取值范围.22.选修4﹣1:几何证明选讲切线AB与圆切于点B,圆内有一点C满足AB=AC,∠CAB的平分线AE交圆于D,E,延长EC交圆于F,延长DC交圆于G,连接FG.(Ⅰ)证明:AC∥FG;(Ⅱ)求证:EC=EG.23.以直角坐标系的原点O为...