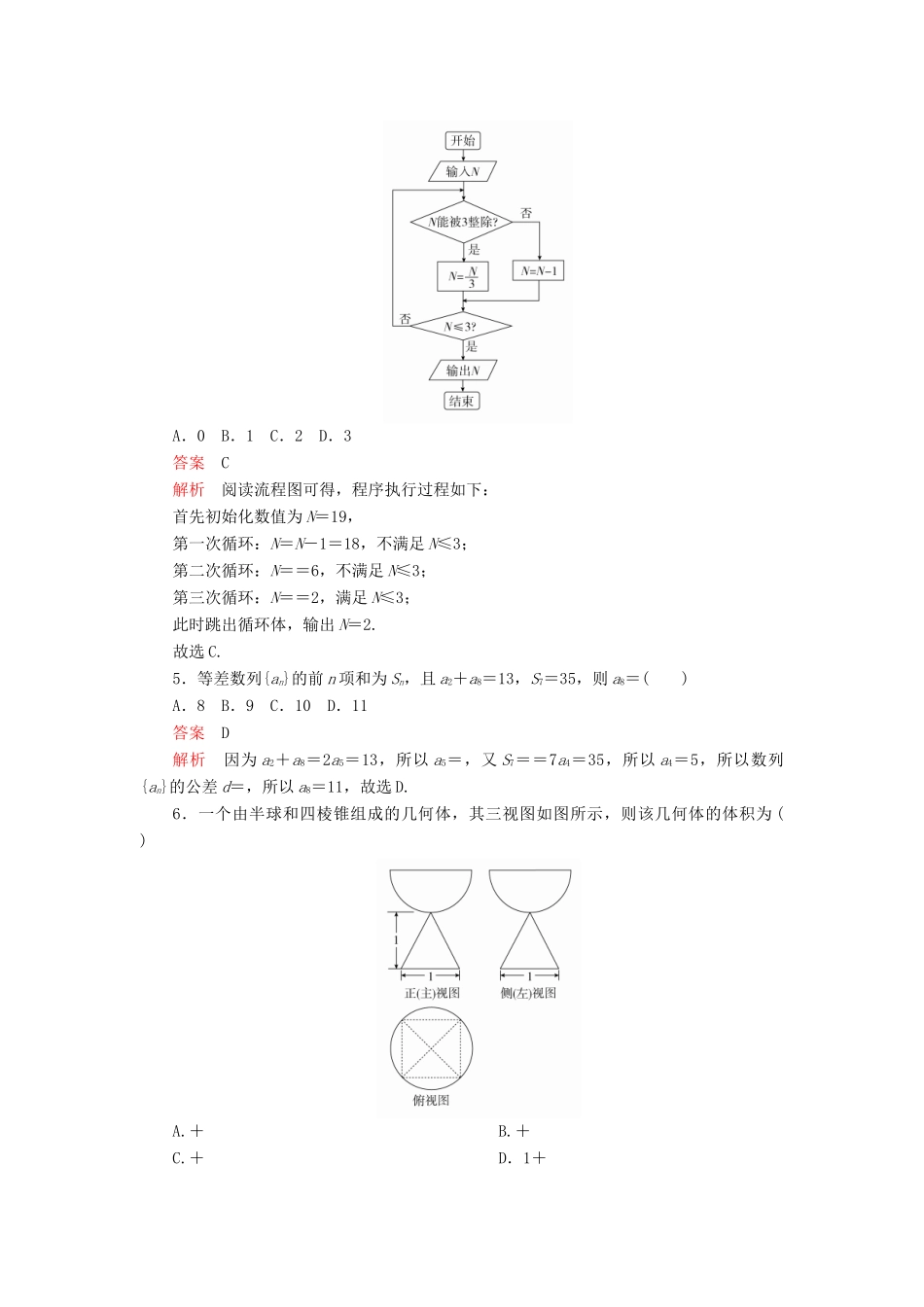
仿真模拟(三)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中只有一项是符合题目要求的.1.已知全集为实数集R,集合A={x|x2-3x<0},B={x|log2x>0},则(∁RA)∩B=()A.(-∞,0]∪(1,+∞)B.(0,1]C.[3,+∞)D.∅答案C解析因为A=(0,3),所以∁RA=(-∞,0]∪[3,+∞).又B=(1,+∞),所以(∁RA)∩B=[3,+∞).2.在复平面内,复数z=所对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限答案A解析z==1+i.3.若x,y满足则2x+y的最大值为()A.0B.3C.4D.5答案C解析画出可行域,如图中阴影部分所示,令z=2x+y,则y=-2x+z,当直线y=-2x+z过点A(1,2)时,z最大,zmax=4.故选C.4.阅读下面的程序框图,运行相应的程序,若输入N的值为19,则输出N的值为()A.0B.1C.2D.3答案C解析阅读流程图可得,程序执行过程如下:首先初始化数值为N=19,第一次循环:N=N-1=18,不满足N≤3;第二次循环:N==6,不满足N≤3;第三次循环:N==2,满足N≤3;此时跳出循环体,输出N=2.故选C.5.等差数列{an}的前n项和为Sn,且a2+a8=13,S7=35,则a8=()A.8B.9C.10D.11答案D解析因为a2+a8=2a5=13,所以a5=,又S7==7a4=35,所以a4=5,所以数列{an}的公差d=,所以a8=11,故选D.6.一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为()A.+B.+C.+D.1+答案C解析由三视图可知四棱锥为正四棱锥,底面正方形的边长为1,四棱锥的高为1,球的直径为正四棱锥底面正方形的外接圆的直径,所以球的直径2R=,则R=,所以半球的体积为R3=,又正四棱锥的体积为×12×1=,所以该几何体的体积为+.故选C.7.已知数列{an}满足a1=0,an+1=(n∈N*),则a20=()A.0B.-C.D.答案B解析易知a1=0,a2=-,a3=,a4=0,a5=-,…所以数列{an}是周期为3的周期性摆动数列.所以a20=a2+18=a2=-.故选B.8.如图,在圆O中,已知弦AB=4,弦AC=6,那么AO·BC的值为()A.10B.2C.D.-10答案A解析如图,延长AO,交圆O于点D,连接BD,CD,则△ACD和△ABD均为直角三角形.于是AO·BC=AD·(BA+AC)=AD·BA+AD·AC=(AB+BD)·BA+(AC+CD)·AC=(-|BA|2+|AC|2)=(-16+36)=10.故选A.9.若双曲线2x2-y2=k的焦距是6,则k的值是()A.6B.±6C.24D.±24答案B解析若k>0,则双曲线的标准方程为-=1,所以a2=,b2=k,c2=,又c=3,所以=9,k=6;若k<0,则双曲线的标准方程为-=1,所以a2=-k,b2=-,c2=-,又c=3,所以-=9,k=-6;综上可知,k=±6.10.中国古代名词“刍童”原来是草堆的意思,关于“刍童”体积计算的描述,《九章算术》注曰:“倍上袤,下袤从之.亦倍下袤,上袤从之.各以其广乘之,并,以高乘之,六而一.”其计算方法是:将上底面的长乘二,与下底面的长相加,再与上底面的宽相乘;将下底面的长乘二,与上底面的长相加,再与下底面的宽相乘;把这两个数值相加与高相乘,再取其六分之一.已知一个“刍童”的下底面是周长为18的矩形,上底面矩形的长为3,宽为2,“刍童”的高为3,则该“刍童”的体积的最大值为()A.B.C.39D.答案B解析设下底面的长为x,则下底面的宽为=9-x.由题可知上底面矩形的长为3,宽为2,“刍童”的高为3,所以其体积V=×3×[(3×2+x)×2+(2x+3)·(9-x)]=-x2++,故当x=时,体积取得最大值,最大值为-2+×+=.故选B.11.已知函数f(x)=x3-4x,若f(x1)=f(x2)=f(x3)=m,其中x1-2B.x+x<4C.x+x<6D.x3>2答案C解析因为f(x)=x3-4x,所以f′(x)=3x2-4,令f′(x)>0,得x<-或x>,令f′(x)<0,得-4,04,x+...