（新课标）高考数学大一轮复习 7.7.2利用空间向量求空间角课时作业 理-人教版高三全册数学试题VIP免费

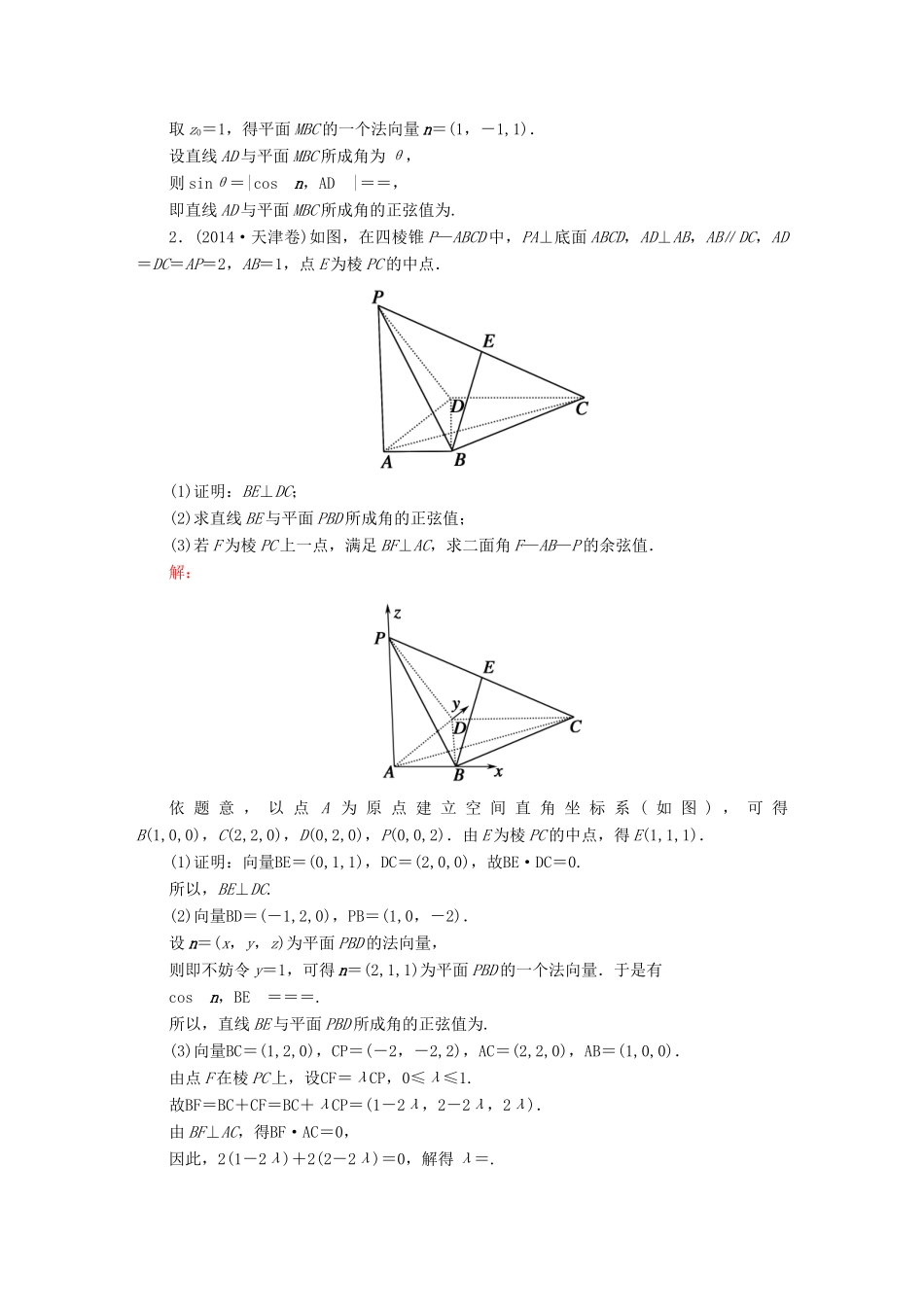
课时作业51利用空间向量求空间角1．(2014·福建卷)在平面四边形ABCD中，AB＝BD＝CD＝1，AB⊥BD，CD⊥BD.将△ABD沿BD折起，使得平面ABD⊥平面BCD，如图．(1)求证：AB⊥CD；(2)若M为AD中点，求直线AD与平面MBC所成角的正弦值．解：(1) 平面ABD⊥平面BCD，平面ABD∩平面BCD＝BD，AB⊂平面ABD，AB⊥BD，∴AB⊥平面BCD.又CD⊂平面BCD，∴AB⊥CD.(2)过点B在平面BCD内作BE⊥BD，如图．由(1)知AB⊥平面BCD，BE⊂平面BCD，BD⊂平面BCD，∴AB⊥BE，AB⊥BD.以B为坐标原点，分别以BE，BD，BA的方向为x轴，y轴，z轴的正方向建立空间直角坐标系．依题意，得B(0,0,0)，C(1,1,0)，D(0,1,0)，A(0,0,1)，M(0，，)，则BC＝(1,1,0)，BM＝(0，，)，AD＝(0,1，－1)．设平面MBC的法向量n＝(x0，y0，z0)，则即取z0＝1，得平面MBC的一个法向量n＝(1，－1,1)．设直线AD与平面MBC所成角为θ，则sinθ＝|cosn，AD|＝＝，即直线AD与平面MBC所成角的正弦值为.2．(2014·天津卷)如图，在四棱锥P—ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，点E为棱PC的中点．(1)证明：BE⊥DC；(2)求直线BE与平面PBD所成角的正弦值；(3)若F为棱PC上一点，满足BF⊥AC，求二面角F—AB—P的余弦值．解：依题意，以点A为原点建立空间直角坐标系(如图)，可得B(1,0,0)，C(2,2,0)，D(0,2,0)，P(0,0,2)．由E为棱PC的中点，得E(1,1,1)．(1)证明：向量BE＝(0,1,1)，DC＝(2,0,0)，故BE·DC＝0.所以，BE⊥DC.(2)向量BD＝(－1,2,0)，PB＝(1,0，－2)．设n＝(x，y，z)为平面PBD的法向量，则即不妨令y＝1，可得n＝(2,1,1)为平面PBD的一个法向量．于是有cosn，BE＝＝＝.所以，直线BE与平面PBD所成角的正弦值为.(3)向量BC＝(1,2,0)，CP＝(－2，－2,2)，AC＝(2,2,0)，AB＝(1,0,0)．由点F在棱PC上，设CF＝λCP，0≤λ≤1.故BF＝BC＋CF＝BC＋λCP＝(1－2λ，2－2λ，2λ)．由BF⊥AC，得BF·AC＝0，因此，2(1－2λ)＋2(2－2λ)＝0，解得λ＝.即BF＝.设n1＝(x，y，z)为平面FAB的法向量，则即不妨令z＝1，可得n1＝(0，－3,1)为平面FAB的一个法向量．取平面ABP的法向量n2＝(0,1,0)，则cosn1，n2＝＝＝－.易知，二面角F—AB—P是锐角，所以其余弦值为.3．在长方体ABCD—A1B1C1D1中，AB＝，AD＝1，M是线段AD的中点．(1)试在平面ABCD内过M点作出与平面A1B1CD平行的直线l，说明理由，并证明：l⊥平面AA1D1D；(2)若(1)中的直线l交直线AC于点N，且二面角A—A1N—M的余弦值为，求AA1的长．解：(1)在平面ABCD内过M点作直线l∥DC， l⊄平面A1B1CD，DC⊂平面A1B1CD，∴l∥平面A1B1CD.在长方体ABCD—A1B1C1D1中，DC⊥AD，DC⊥DD1，则l⊥AD，l⊥DD1.又AD∩DD1＝D，∴l⊥平面AA1D1D.(2)由(1)知，l∥DC且M是线段AD的中点，∴N是线段AC的中点．设AA1＝h，以A1为坐标原点，分别以A1B1，A1D1，A1A所在直线为x轴，y轴，z轴，建立空间直角坐标系A1—xyz.则A1(0,0,0)，A(0,0，h)，N(，，h)，M(0，，h)．∴A1A＝(0,0，h)，A1N＝(，，h)，A1M＝(0，，h)，MN＝(，0,0)．设平面A1AN的法向量n1＝(x1，y1，z1)，则，∴，取x1＝1，∴n1＝(1，－，0)．设平面A1MN的法向量n2＝(x2，y2，z2)，则，∴，取z2＝1，∴n2＝(0，－2h,1)． 二面角A—A1N—M的余弦值为，∴cos〈n1，n2〉＝，即＝，∴＝，解得h＝1，即AA1＝1.1．等边三角形ABC的边长为3，点D、E分别是边AB、AC上的点，且满足＝＝(如图1)．将△ADE沿DE折起到△A1DE的位置，使二面角A1—DE—B为直二面角，连接A1B、A1C(如图2)．(1)求证：A1D⊥平面BCED；(2)在线段BC上是否存在点P，使直线PA1与平面A1BD所成的角为60°？若存在，求出PB的长，若不存在，请说明理由．解：(1)证明：因为等边△ABC的边长为3，且＝＝，所以AD＝1，AE＝2.在△ADE中，∠DAE＝60°，由余弦定理得DE＝＝.因为AD2＋DE2＝AE2，所以AD⊥DE.折叠后有A1D⊥DE，因为二面角A1—DE—B是直二面角，所以平面A1DE⊥平面BCED，又平面A1DE∩平面BCED＝DE，A1D⊂平面A1DE，A1D⊥DE，所以A1D⊥平面BCED.(2)由(1)的证明，可知ED⊥DB，A1D⊥平面BCED，以D为坐标原点，以射线DB、DE、DA1分别为x轴、y轴、z轴的正半轴，建立空间直角坐标系D—xyz如...