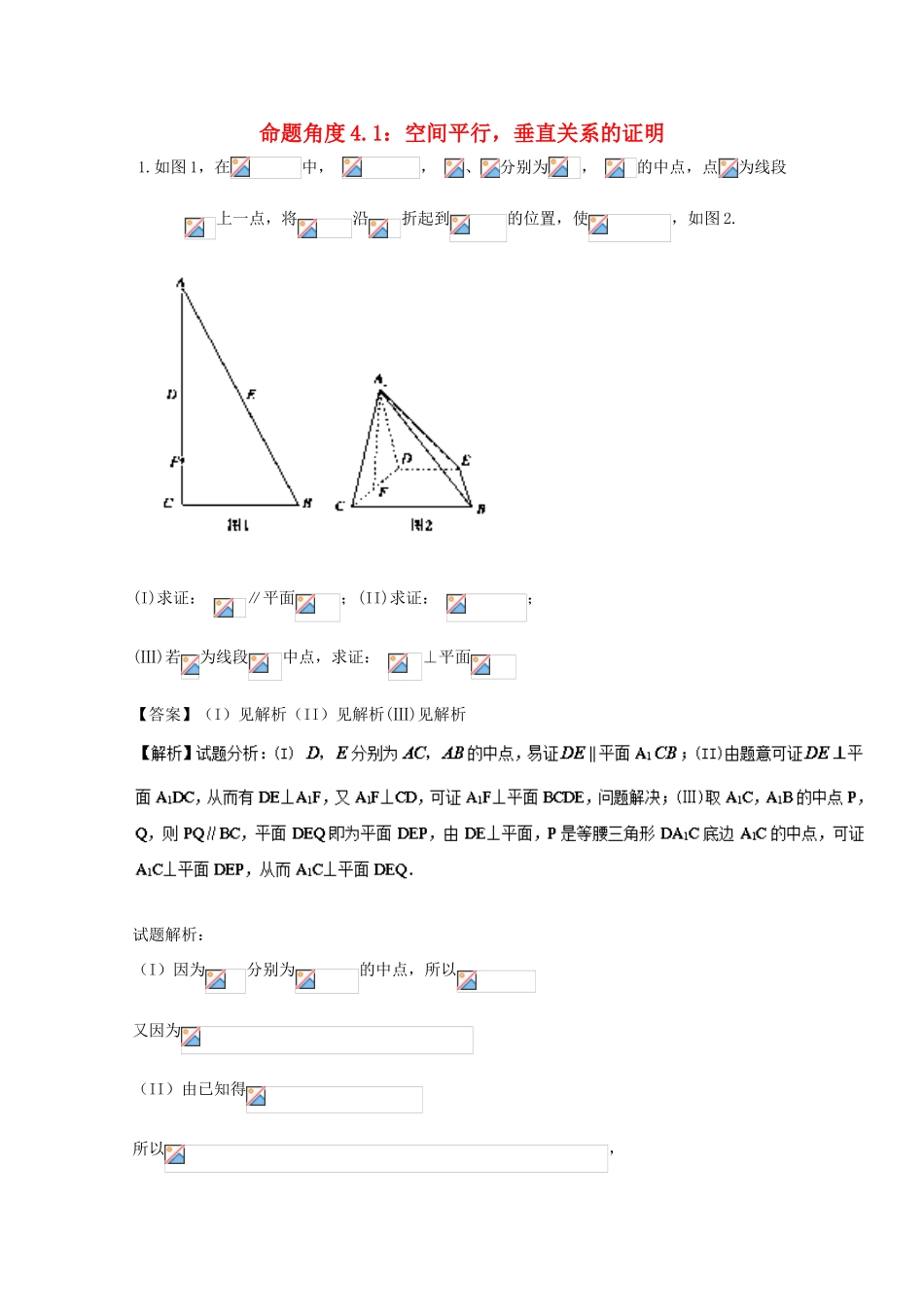
命题角度4.1:空间平行,垂直关系的证明1.如图1,在中,,、分别为,的中点,点为线段上一点,将沿折起到的位置,使,如图2.(I)求证:∥平面;(II)求证:;(Ⅲ)若为线段中点,求证:⊥平面【答案】(I)见解析(II)见解析(Ⅲ)见解析试题解析:(I)因为分别为的中点,所以又因为(II)由已知得所以,,又因为所以点睛:本题考查直线与平面平行的判定,直线与平面垂直的判定与性质,对空间想象能力有很高要求.2.如图,在三棱锥中,已知平面平面.(1)若,求证:;(2)若过点作直线平面,求证:平面.【答案】(1)见解析(2)见解析【解析】【试题分析】(1)依据题设借助面面垂直的性质定理证明平面平面,然后运用线面垂直的性质定理证明;(2)借助题设条件先证明平面,进而确定,然后再运用线面平行的性质定理推证:证明:(1)因为平面平面,平面平面,平面,,所以平面.因为平面,所以.又因为平面所以平面又因为平面所以.3.如图,在四棱锥中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.(1)求到平面的距离(2)在线段上是否存在一点,使?若存在,求出的值;若不存在,说明理由.【答案】(I)(II)见解析.【解析】试题分析:(1)利用等体积法结合题意可求得到平面的距离为;(2)当时满足题意,利用题中所给的条件进行证明即可.试题解析:解:(1)方法一:因为平面,,又,所以平面,又,所以到平面的距离为.方法二:等积法求高.4.如图,四棱柱中,平面,,,为的中点.(Ⅰ)证明:;(Ⅱ)若,,求证:平面平面.【答案】(I)详见解析;(II)详见解析.【解析】试题分析:(Ⅰ)分别取的中点,连结,可证明四边形是平行四边形,所有又根据中,中位线的性质,,根据平行线的传递性可知;(Ⅱ)根据条件可证明,所有平面,即,也可证明,所有平面,即证明了平面平面.试题解析:(Ⅰ)分别取中的中点为,并连接,则由,得,,,可得四边形为平行四边形,那么,,又,,所以,且,得四边形是平行四边形,可得,又,所以.(Ⅱ)取中点,连接,则,可得,则,即,,那么,又,得平面,那么,由,得,又,那么,同理,,即得,可得平面,即得平面平面.【点睛】本题考查了平行与垂直的证明,而垂直的证明是难点,若是证明线线垂直,一般转化为证明线面垂直,线线垂直,或是三边满足勾股定理,证明线线垂直;若是证明线面垂直,一般根据判断定理,证明线与平面内的两条相交直线垂直,则线面垂直;若是证明面面垂直,同样是根据判断定理转化为证明线面垂直,则面面垂直.5.如图,四边形与均为平行四边形,分别是的中点.(1)求证:平面;(2)求证:平面平面.【答案】(1)见解析(2)见解析【解析】试题分析:(1)连接,结合题意证得,利用线面平行的判断定理即可证得平面.(2)结合题意首先证得线面平行:平面,平面,且与为平面内的两条相交直线,据此可得平面平面.(2)因为分别为平行四边形的边的中点,所以,又平面,平面,所以平面.又为中点,所以为的中位线,所以,又平面,平面,所以平面,又与为平面内的两条相交直线,所以平面平面.点睛:证明两个平面平行的方法有:①用定义,此类题目常用反证法来完成证明;②用判定定理或推论(即“线线平行⇒面面平行”),通过线面平行来完成证明;③根据“垂直于同一条直线的两个平面平行”这一性质进行证明;④借助“传递性”来完成.6.在正方体中,分别是的中点.(1)证明:平面平面;(2)棱上是否存在点,使平面?请证明你的结论.【答案】(1)见解析(2)在棱上取点,使得,则平面.【解析】试题分析:(1)证明平面平面,可先证明平面,可先证明,.(2)延长,交于,连交于,得且,四边形为平行四边形,所以,即.即证得平面试题解析:(2)解:在棱上取点,使得,则平面.证明如下:延长,交于,连交于.因为,为中点,所以为中点.因为,所以,且.因为,为中点,所以且,即四边形为平行四边形,所以,即.又平面,平面,所以平面.点睛:存在性问题,可以由果索因,找出所求点的位置,写过程时把结论先写上,利用这一条件证出结果.7.如图,在多面体中,平面平面,四边形是菱形,四边形是矩形,,是的中点.(1)求证:平面;...