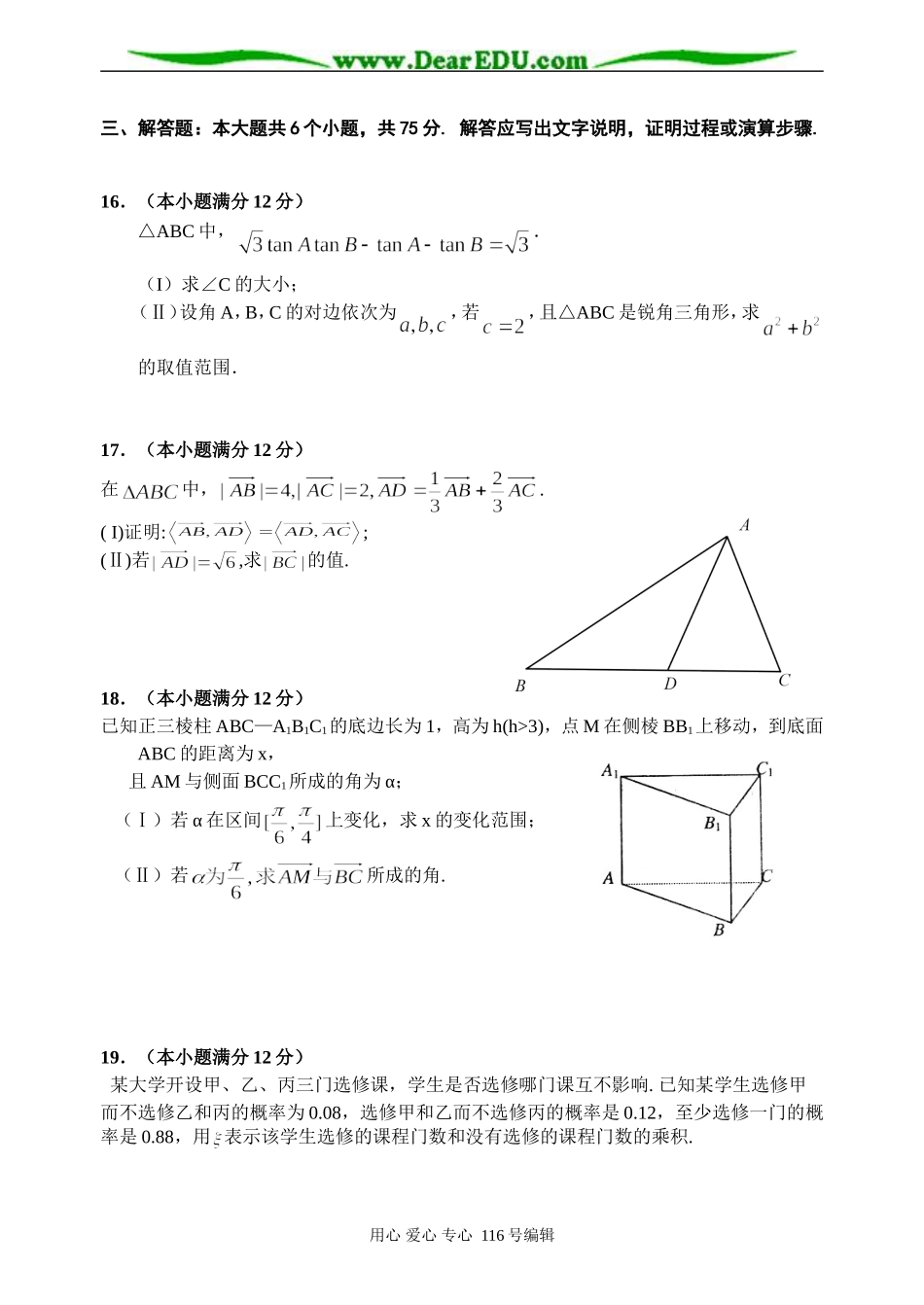
孝昌二中期末考试理科数学试卷温馨提示:好好活就是干有意义的事情一、选择题:本大题共10小题,每小题5分,共50分.1、设A、B是两个集合,定义,R},则M-N=(★★★)A.[-3,1]B.[-3,0)C.[0,1]D.[-3,0]2、函数在同一直角坐标系下的图象大致是(★★★)3、已知正方体--中,M为AB中点,棱长为2,P是底面ABCD上的动点,且满足条件,则动点P在底面ABCD上形成的轨迹是(★★★)A.圆B.椭圆C.双曲线D.抛物线4、如图,平面内的两条相交直线和将该平面分割成四个部分I、II、III、Ⅳ(不包含边界)。设,且点P落在第III部分,则实数m,n满足(★★★)A.B.C.D.5.等差数列中,,若数列的前项和为,则的值为(★★★)A、14B、15C、16D、186.方程满足且0<,则实数a的取值范围是(★★★)A.B.C.D.用心爱心专心116号编辑7.已知,则的值(★★★)A、随的增大而增大B、有时随的增大而增大,有时随的增大而减小C、随的增大而减小D、是一个与无关的常数8.从集合中任取三个数排成一列,则这三个数成等差数列的概率是(★★★)A、B、C、D、9.称为两个向量、间的“距离”.若向量、满足:①;②;③对任意的,恒有则(★★★)A、B、C、D、10.已知双曲线的左、右顶点分别为A、B,双曲线在第一象限的图像上有一点P,,则(★★★)A、B、C、D、二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.11.设,则(请把答案填写在答题卷上).12.设(其中是虚数单位),则展开式中的第4项是(请把答案填写在答题卷上).13.约束条件:,目标函数的最小值是(请把答案填写在答题卷上).14.已知椭圆的右焦点为过作与轴垂直的直线与椭圆相交于点,过点的椭圆的切线与轴相交于点,则点的坐标为(请把答案填写在答题卷上).15.已知集合,对它的非空子集A,先将A中的每个元素分别乘以,再求和(如A={1,3,6},可求得和为),则对M的所有非空子集,这些和的总和是(请把答案填写在答题卷上).用心爱心专心116号编辑三、解答题:本大题共6个小题,共75分.解答应写出文字说明,证明过程或演算步骤.16.(本小题满分12分)△ABC中,.(I)求∠C的大小;(Ⅱ)设角A,B,C的对边依次为,若,且△ABC是锐角三角形,求的取值范围.17.(本小题满分12分)在中,.(I)证明:;(Ⅱ)若,求的值.18.(本小题满分12分)已知正三棱柱ABC—A1B1C1的底边长为1,高为h(h>3),点M在侧棱BB1上移动,到底面ABC的距离为x,且AM与侧面BCC1所成的角为α;(Ⅰ)若α在区间上变化,求x的变化范围;(Ⅱ)若所成的角.19.(本小题满分12分)某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知某学生选修甲而不选修乙和丙的概率为0.08,选修甲和乙而不选修丙的概率是0.12,至少选修一门的概率是0.88,用表示该学生选修的课程门数和没有选修的课程门数的乘积.用心爱心专心116号编辑(I)记“函数为R上的偶函数”为事件A,求事件A的概率;(Ⅱ)求的分布列和数学期望.20.(本小题满分13分)已知椭圆的右准线与轴相交于点,右焦点到上顶点的距离为,点是线段上的一个动点.(I)求椭圆的方程;(Ⅱ)是否存在过点且与轴不垂直的直线与椭圆交于、两点,使得,并说明理由.21.(本小题满分14分)已知函数求:(I)求证:函数的图象关于点中心对称,并求的值;(II)设,且1<a1<2,求证+…+<2.孝昌二中理科数学知识·数学能力检测卷(十二)参考答案1.B2.D3.A4.B5.C6.D7.A8.B9.C10.C用心爱心专心116号编辑11.212.13.014.15.9616.解:(1)依题意:,即,又,∴,∴,(2)由三角形是锐角三角形可得,即。由正弦定理得∴,∴, ,∴,∴即。17.设,则=,,,又,.(2)=,18.解:(I)设BC的中点为D,连结AD、DM,在正△ABC中,易知AD⊥BC,又侧面BCC1与底面ABC互相垂直,∴AD⊥平面BCC1,即∠AMD为AM与侧面BCC1所成的角,∴∠AMD=α,用心爱心专心116号编辑∴在Rt△ADM中,cosAMD=依题意BM即为点B到度面ABC的距离,∴BM=x,且,由已知即x的变化范围是;(II)19.20.解:设该学生选修甲、乙、丙的概率分别为x、y、z依题意得…………4分(1)若函数为R上的偶函数,则=0…………5分当=0时,表示该学生选修三门功课或三门功...