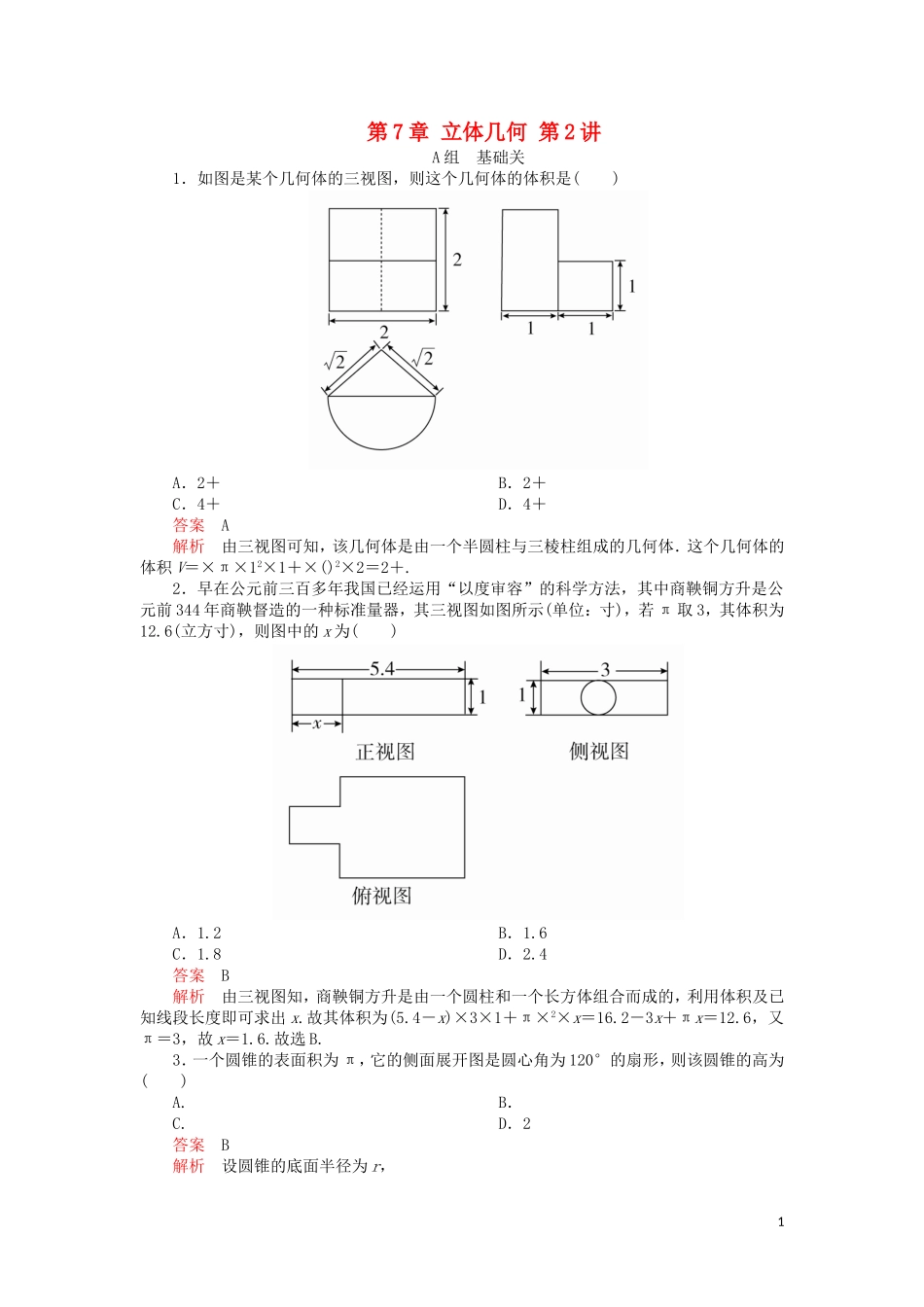
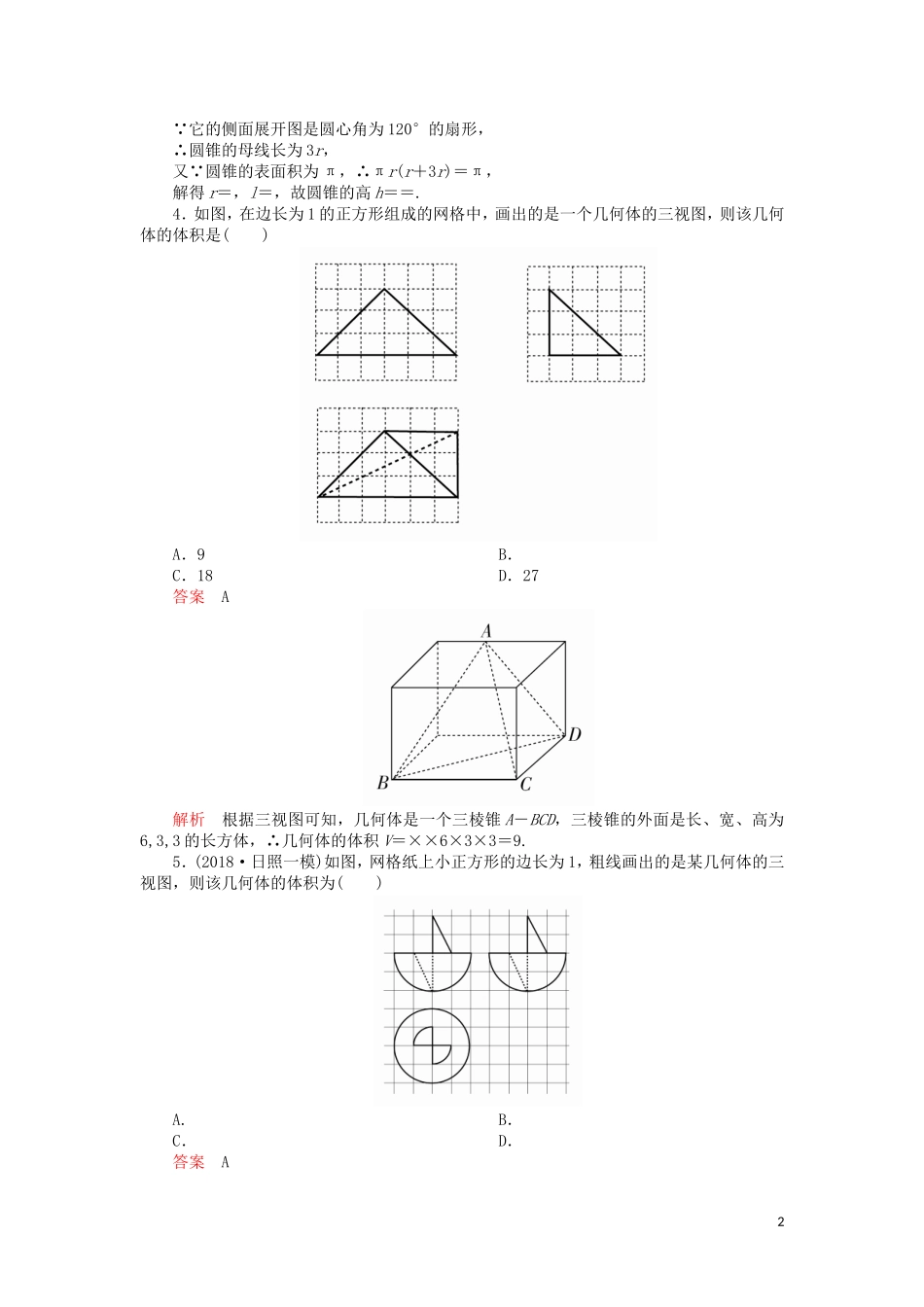
第7章立体几何第2讲A组基础关1.如图是某个几何体的三视图,则这个几何体的体积是()A.2+B.2+C.4+D.4+答案A解析由三视图可知,该几何体是由一个半圆柱与三棱柱组成的几何体.这个几何体的体积V=×π×12×1+×()2×2=2+.2.早在公元前三百多年我国已经运用“以度审容”的科学方法,其中商鞅铜方升是公元前344年商鞅督造的一种标准量器,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为()A.1.2B.1.6C.1.8D.2.4答案B解析由三视图知,商鞅铜方升是由一个圆柱和一个长方体组合而成的,利用体积及已知线段长度即可求出x.故其体积为(5.4-x)×3×1+π×2×x=16.2-3x+πx=12.6,又π=3,故x=1.6.故选B.3.一个圆锥的表面积为π,它的侧面展开图是圆心角为120°的扇形,则该圆锥的高为()A.B.C.D.2答案B解析设圆锥的底面半径为r,1 它的侧面展开图是圆心角为120°的扇形,∴圆锥的母线长为3r,又 圆锥的表面积为π,∴πr(r+3r)=π,解得r=,l=,故圆锥的高h==.4.如图,在边长为1的正方形组成的网格中,画出的是一个几何体的三视图,则该几何体的体积是()A.9B.C.18D.27答案A解析根据三视图可知,几何体是一个三棱锥A-BCD,三棱锥的外面是长、宽、高为6,3,3的长方体,∴几何体的体积V=××6×3×3=9.5.(2018·日照一模)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为()A.B.C.D.答案A2解析该几何体可以看成是在一个半球上叠加一个圆锥,然后挖掉一个相同的圆锥,所以该几何体的体积和半球的体积相等.由图可知,球的半径为2,则V=πr3=.故选A.6.(2018·江西九江一模)如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的表面积为()A.6+4+2B.8+4C.6+6D.6+2+4答案A解析直观图是四棱锥P-ABCD,如图所示,S△PAB=S△PAD=S△PDC=×2×2=2,S△PBC=×2×2×sin60°=2,S四边形ABCD=2×2=4,因此所求棱锥的表面积为6+4+2.故选A.7.(2017·衡水中学三调)已知正方体ABCD-A′B′C′D′的外接球的体积为,将正方体割去部分后,剩余几何体的三视图如图所示,则剩余几何体的表面积为()A.+B.3+或+C.2+D.+或2+答案B解析设正方体的棱长为a,依题意得,×=,解得a=1.由三视图可知,该几何体的直观图有以下两种可能,图1对应的几何体的表面积为+,图2对应的几何体的表面积为3+.故选B.38.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为________.答案7解析设圆台较小底面半径为r,则另一底面半径为3r.由S=π(r+3r)·3=84π,解得r=7.9.已知在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是________.答案解析如图,设A1C1∩B1D1=O1, B1D1⊥A1O1,B1D1⊥AA1,∴B1D1⊥平面AA1O1,故平面AA1O1⊥平面AB1D1,交线为AO1,在平面AA1O1内过A1作A1H⊥AO1于H,则易知A1H的长即是点A1到截面AB1D1的距离,在Rt△A1O1A中,A1O1=,AO1=3,由A1O1·A1A=h·AO1,可得A1H=.10.我国古代数学经典名著《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的三棱锥称为鳖臑(biēnào).若三棱锥P-ABC为鳖臑,且PA⊥平面ABC,PA=AB=2,且该鳖臑的外接球的表面积为24π,则该鳖臑的体积为________.答案4解析根据题意,三棱锥P-ABC为鳖臑,且PA⊥平面ABC,PA=AB=2,如图所示,可得∠PAB=∠PAC=∠ABC=∠PBC=90°.易知PC为外接球的直径,设外接球的半径为R.又该鳖臑的外接球的表面积为24π,则R2==6,则BC==4,则该鳖臑的体积为××2×4×2=.B组能力关1.(2018·山西五校3月联考)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈;上袤二丈,无广;高一丈,问:积几何?”其意思为:“今有底面为矩形的屋脊柱的楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈,问它的体积是多少?”已知1丈为10尺,现将该楔体的三视图给出,其中网格纸上小正方形的边长为1丈...