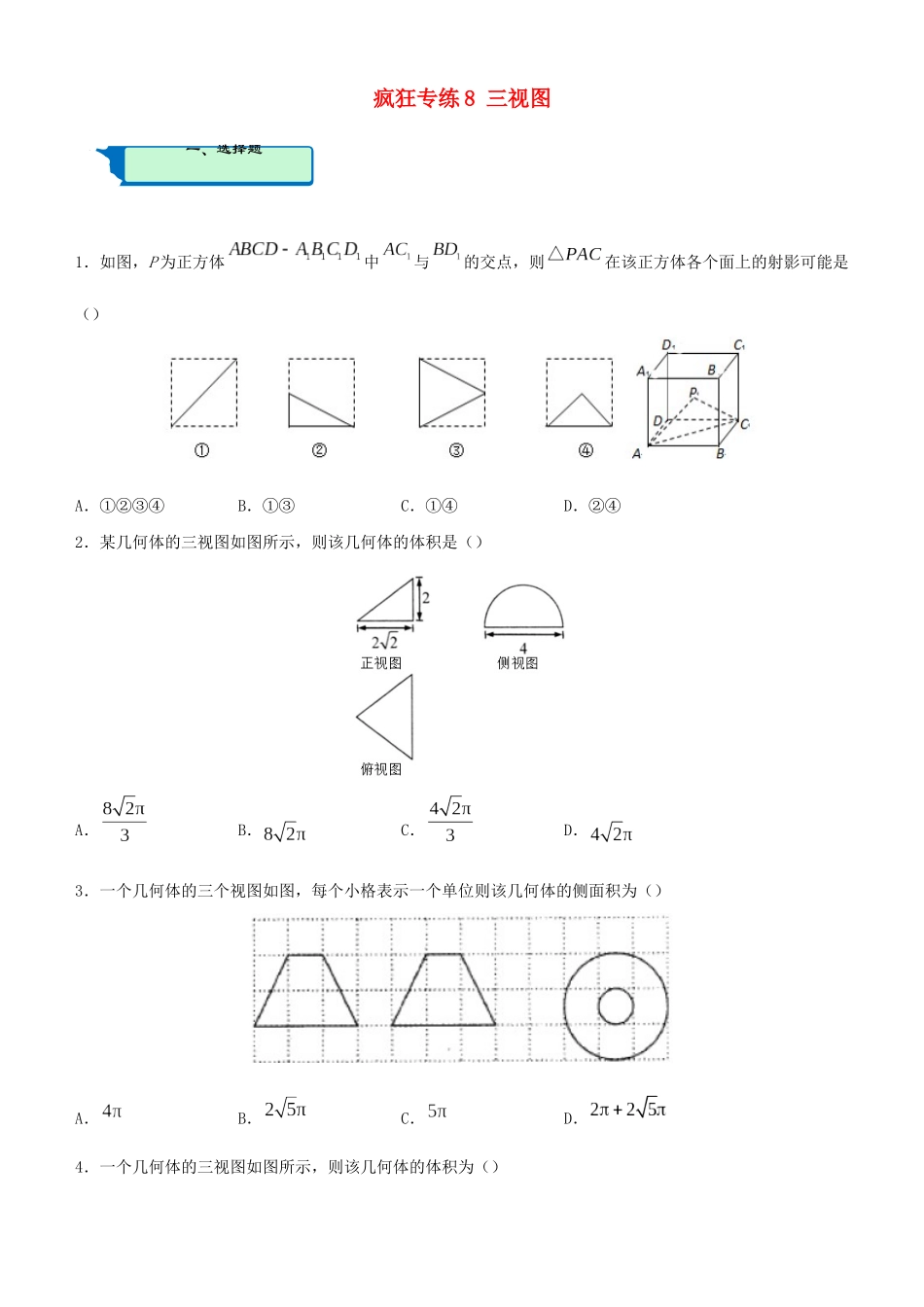
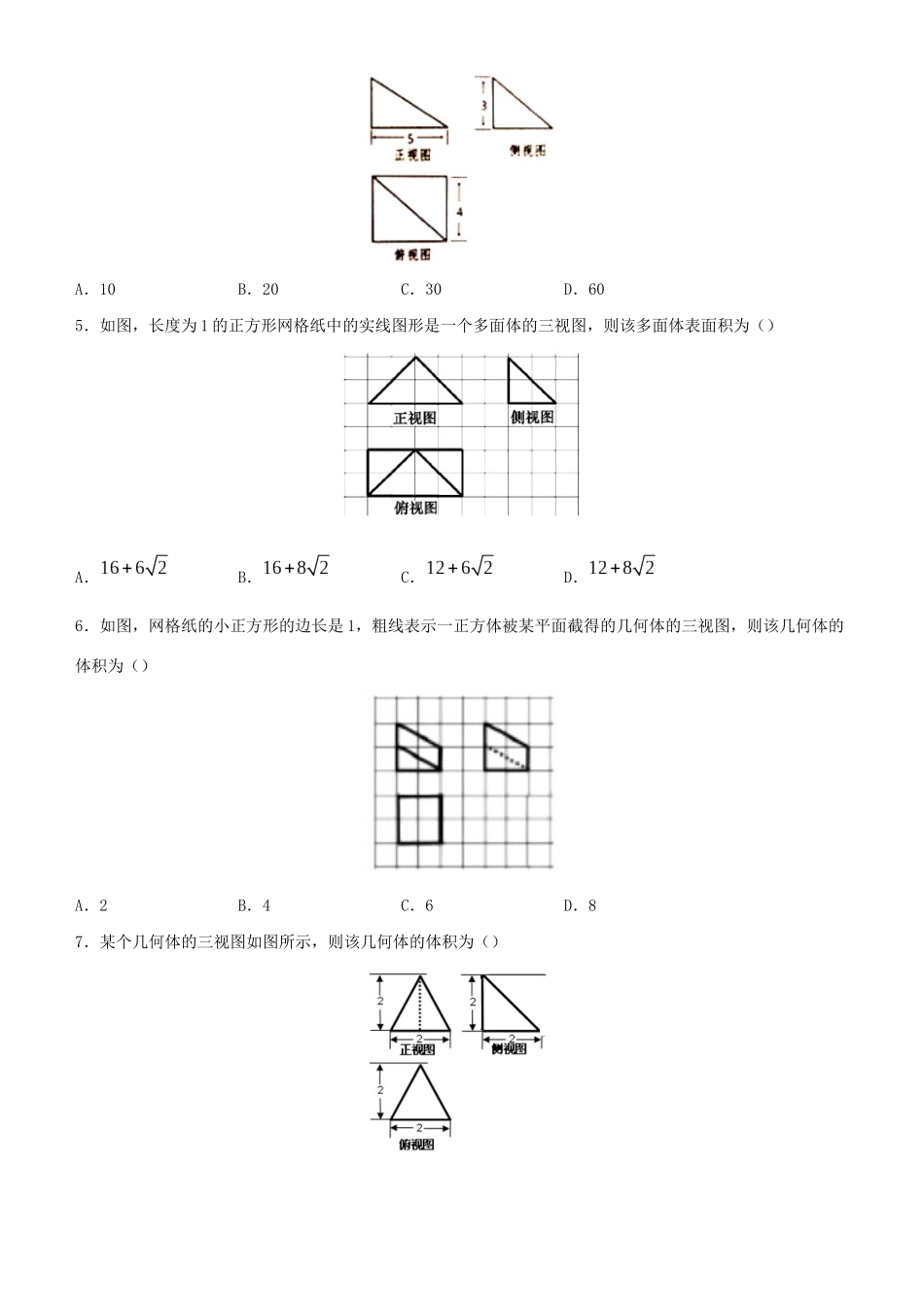
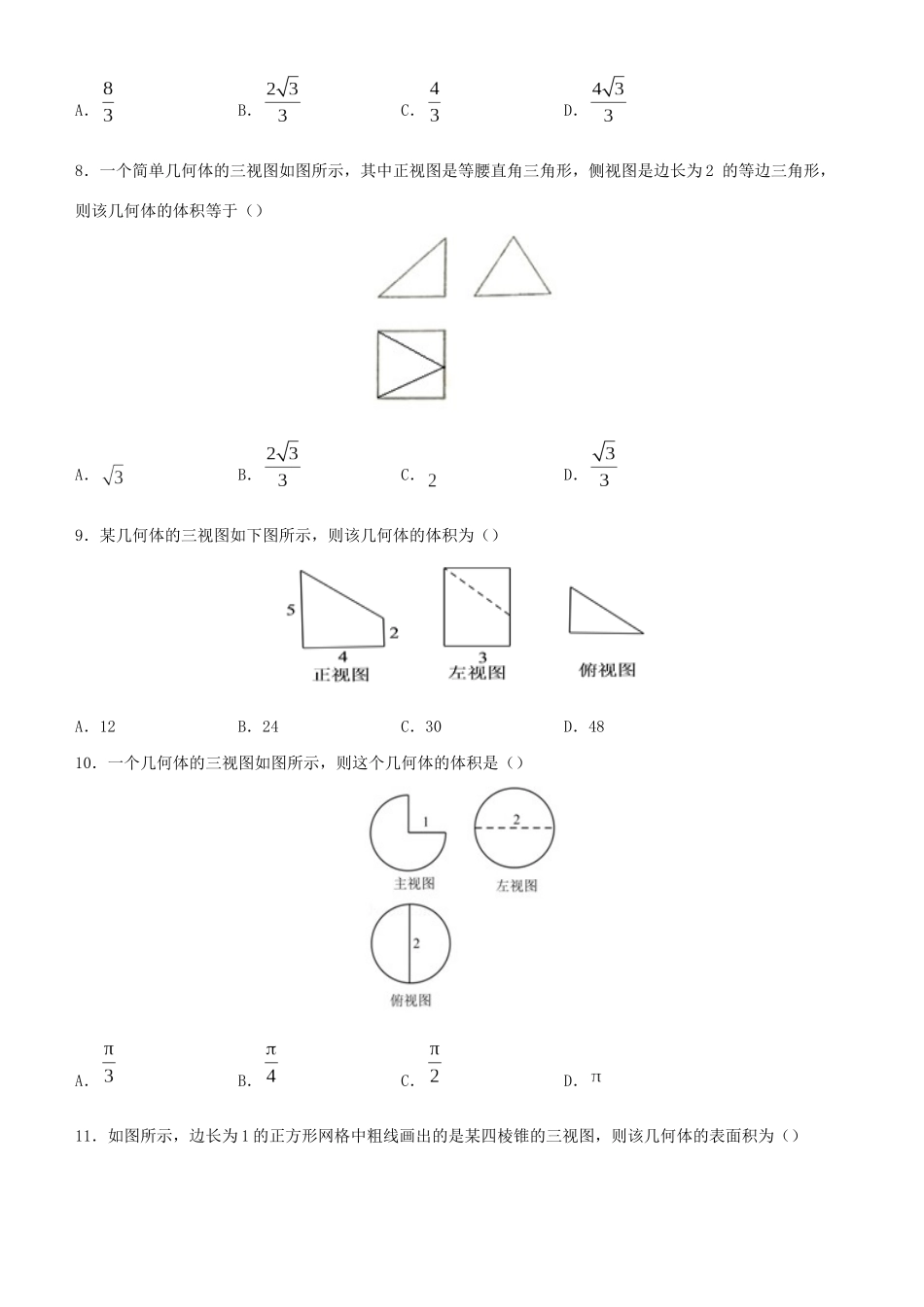
一、选择题疯狂专练8三视图1.如图,P为正方体中与的交点,则在该正方体各个面上的射影可能是()A.①②③④B.①③C.①④D.②④2.某几何体的三视图如图所示,则该几何体的体积是()A.B.C.D.3.一个几何体的三个视图如图,每个小格表示一个单位则该几何体的侧面积为()A.B.C.D.4.一个几何体的三视图如图所示,则该几何体的体积为()A.10B.20C.30D.605.如图,长度为1的正方形网格纸中的实线图形是一个多面体的三视图,则该多面体表面积为()A.B.C.D.6.如图,网格纸的小正方形的边长是1,粗线表示一正方体被某平面截得的几何体的三视图,则该几何体的体积为()A.2B.4C.6D.87.某个几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.8.一个简单几何体的三视图如图所示,其中正视图是等腰直角三角形,侧视图是边长为2的等边三角形,则该几何体的体积等于()A.B.C.D.9.某几何体的三视图如下图所示,则该几何体的体积为()A.12B.24C.30D.4810.一个几何体的三视图如图所示,则这个几何体的体积是()A.B.C.D.11.如图所示,边长为1的正方形网格中粗线画出的是某四棱锥的三视图,则该几何体的表面积为()二、填空题A.B.C.8D.1212.某多面体的三视图如图所示,其中正视图和侧视图都是由长方形及其一条对角线组成,长方形的宽为3,俯视图为等腰直三角形,直角边长为4,则该多面体的体积是()A.8B.12C.16D.2413.一个四面体的三视图如图所示,则该四面体四个面当中最大面的面积是______.14.用若干块相同的小正方体搭成一个几何体,该几何体的三视图如图所示,则搭成该几何体需要的小正方体的块数是__________.15.如图,网络纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的外接球的表面积为________.16.网格纸上小正方形的边长为,粗实线画出的是某四面体的三视图,则该四面体最大侧棱长为_________.答案与解析一、选择题1.【答案】C【解析】由题意知,P为正方体ABCD﹣A1B1C1D1的中心,则从上向下投影时,点P的影子落在对角线AC上,故△PAC在下底面上的射影是线段AC,是第一个图形;当从前向后投影时,点P的影子应落在侧面CDC1D1的中心上,A点的影子落在D上,故故△PAC在面CDC1D1上的射影是三角形,是第四个图形;当从左向右投影时,点P的影子应落在侧面BCB1C1的中心上,A点的影子落在B上,故故△PAC在面CDC1D1上的射影是三角形,是第四个图形.故选C.2.【答案】C【解析】通过三视图可以判断该几何是底面半径为2、高为的圆锥的一半,因此所求几何体的体积为:,故本题选C.3.【答案】B【解析】由三视图可知该几何体是一个圆台,上底面直径为1,下底面直径为3,高为2,则母线,所以该几何体的侧面积为,故选B.4.【答案】B【解析】由三视图可知,该几何体为底面为长为,宽为的长方形,高为的四棱锥,四棱锥体积,本题正确选项B.5.【答案】D【解析】由三视图还原原几何体如图,该几何体为四棱锥,底面是矩形,,,四棱锥的高为2.则其表面积为.故选D.6.【答案】B【解析】由题意,直观图如图所示,由图可知该几何体的体积为为正方体的一半,即为,故选B.7.【答案】C【解析】由三视图可知,几何体为高为的三棱锥,三棱锥体积,本题正确选项C.8.【答案】C【解析】由三视图可知几何体为四棱锥,其中底面为矩形,顶点在底面的射影为的中点,由左视图可知棱锥高,,因为正视图为等腰三角形,所以,所以棱锥的体积为,故选C.9.【答案】B【解析】由三视图可知其直观图如下图所示:其由三棱柱截去一个三棱锥所得.三棱柱的体积,三棱锥的体积,故该几何体的体积为24,故选B.10.【答案】D【解析】由三视图可知:该几何体为球的,其半径为1,则体积,故选D.11.【答案】B【解析】表面积为,故选B.二、填空题12.【答案】C【解析】由三视图知,该几何体是四棱锥,故(或),故选C.13.【答案】【解析】由三视图可知,该四面体为,放在正方体中,由直观图可知,面积最大的面为,在正三角形中,,所以其面积,故答案为.14.【答案】【解析】由正视图和侧视图,知该几何体由两层小正方体...