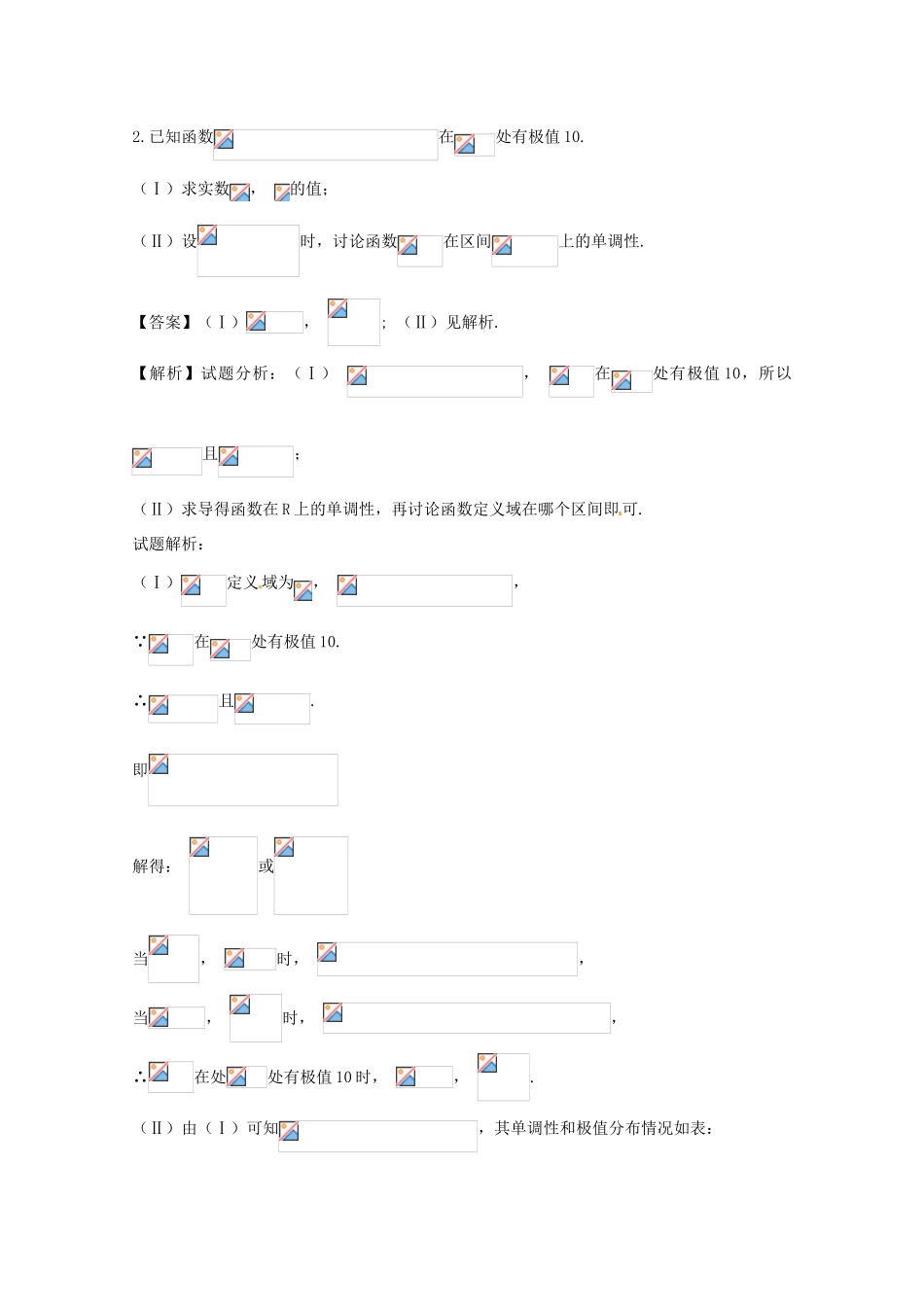
命题角度1:利用导数研究函数的单调性问题1.已知函数.(1)求函数图象上所有点处的切线的倾斜角范围;(2)若,讨论的单调性.【答案】(1);(2)当时,在上单调递增,当时,在上单调递增;在上单调递减.试题解析:(1)函数的定义域为,,当且仅当时,等号成立,切线的倾斜角.(2).∴,令,,当时,,方程两实根为,∴时,,∴,所以在上单调递增;当时,,方程两实根为,且所以在上单调递增;在上单调递减;当时,,在上恒成立,所以在上单调递增.故当时,在上单调递增;当时,在上单调递增;在上单调递减.考点:函数导数与不等式.【方法点晴】解答此类问题,应该首先确定函数的定义域,否则,写出的单调区间易出错.解决含参数问题及不等式问题注意两个转化:(1)利用导数解决含有参数的单调性问题可将问题转化为不等式恒成立问题,要注意分类讨论和数形结合思想的应用.(2)将不等式的证明、方程根的个数的判定转化为函数的单调性问题处理.2.已知函数在处有极值10.(Ⅰ)求实数,的值;(Ⅱ)设时,讨论函数在区间上的单调性.【答案】(Ⅰ),;(Ⅱ)见解析.【解析】试题分析:(Ⅰ),在处有极值10,所以且;(Ⅱ)求导得函数在R上的单调性,再讨论函数定义域在哪个区间即可.试题解析:(Ⅰ)定义域为,, 在处有极值10.∴且.即解得:或当,时,,当,时,,∴在处处有极值10时,,.(Ⅱ)由(Ⅰ)可知,其单调性和极值分布情况如表:1+0-0+增极大减极小增①当且,即时,在区间上单调递减;②当,即时,在区间上的单调递减,在区间上单调递增;点睛:研究函数极值,首先研究导函数的零点,再结合导数的正负即可确定极值;导数为正时函数单调递增,导数为负时单调递减,若函数单调性确定,定义域不定时,只需讨论定义域与单调区间的关系即可.3.已知函数.(Ⅰ)若,求曲线在点处的切线方程;(Ⅱ)当时,讨论函数的单调性.【答案】(I);(II);(III)详见解析.【解析】试题分析:(Ⅰ)求出当的函数的导数,求得切线的斜率和切点,由点斜式方程,即可得到所求切线方程;(Ⅱ)求出函数的导数,求出的零点或,分别对两个零点的大小关系作为分类讨论,即可得到函数的单调性.试题解析:解:(Ⅰ)当时,,∴切线的斜率,又,在点处的切线方程为,即.(Ⅱ).令,得或,①当时,恒成立,∴在上单调递增;②当时,,由,得或;由,得.∴单调递增区间为,;单调减区间为.③当时,,由,得或;由,得.∴单调增区间为,,单调减区间为.综上所述:当时,在上单调递增;当时,单调增区间为,,单调减区间为;当时,单调增区间为,,单调减区间为.4.设函数,的图象在点处的切线与直线平行.(1)求的值;(2)若函数(),且在区间上是单调函数,求实数的取值范围.【答案】(1);(2).【解析】试题分析:(1)根据切线的斜率,求出b的值即可;(2)求出的导数,在上为单调递减函数,等价于在上恒成立,即在上恒成立,构造求最值即可.试题解析:(1)由题意知,曲线在点处的切线斜率为3,所以,又,即,所以.(2)由(1)知,所以,若在上为单调递减函数,则在上恒成立,即,所以.令,则,由,得,,得,故在上是减函数,在上是增函数,则,无最大值,在上不恒成立,故在不可能是单调减函数.若在上为单调递增函数,则在上恒成立,即,所以,由前面推理知,的最小值为,∴,故的取值范围是.点晴:本题主要考查用导数研究函数的单调性,不等式恒成立问题.在上为单调递减函数,等价于在上恒成立,通过变量分离可转化为在上恒成立,先构造即可.4.已知函数.(Ⅰ)讨论的单调性;(Ⅱ)设,若对,,求的取值范围.【答案】(Ⅰ)见解析;(Ⅱ)【解析】试题分析:(Ⅰ)求出的定义域为,求导数,若,若,判断导函数的符号,然后推出函数的单调性;(Ⅱ)不妨设,而,由(Ⅰ)知,在上单调递增,从而,等价于,,令,通过函数的导数求解函数的最值,推出结果.(Ⅱ)不妨设,而,由(Ⅰ)知,在上单调递增,∴.从而,等价于,①,令,则,因此,①等价于在上单调递减,∴对恒成立,∴对恒成立,∴.又,当且仅当,即时,等号成立,∴,故的取值范围为.点睛:本题考查导数知识的运用,考...