高考数学复习点拨 幂函数常见题型例析VIP免费

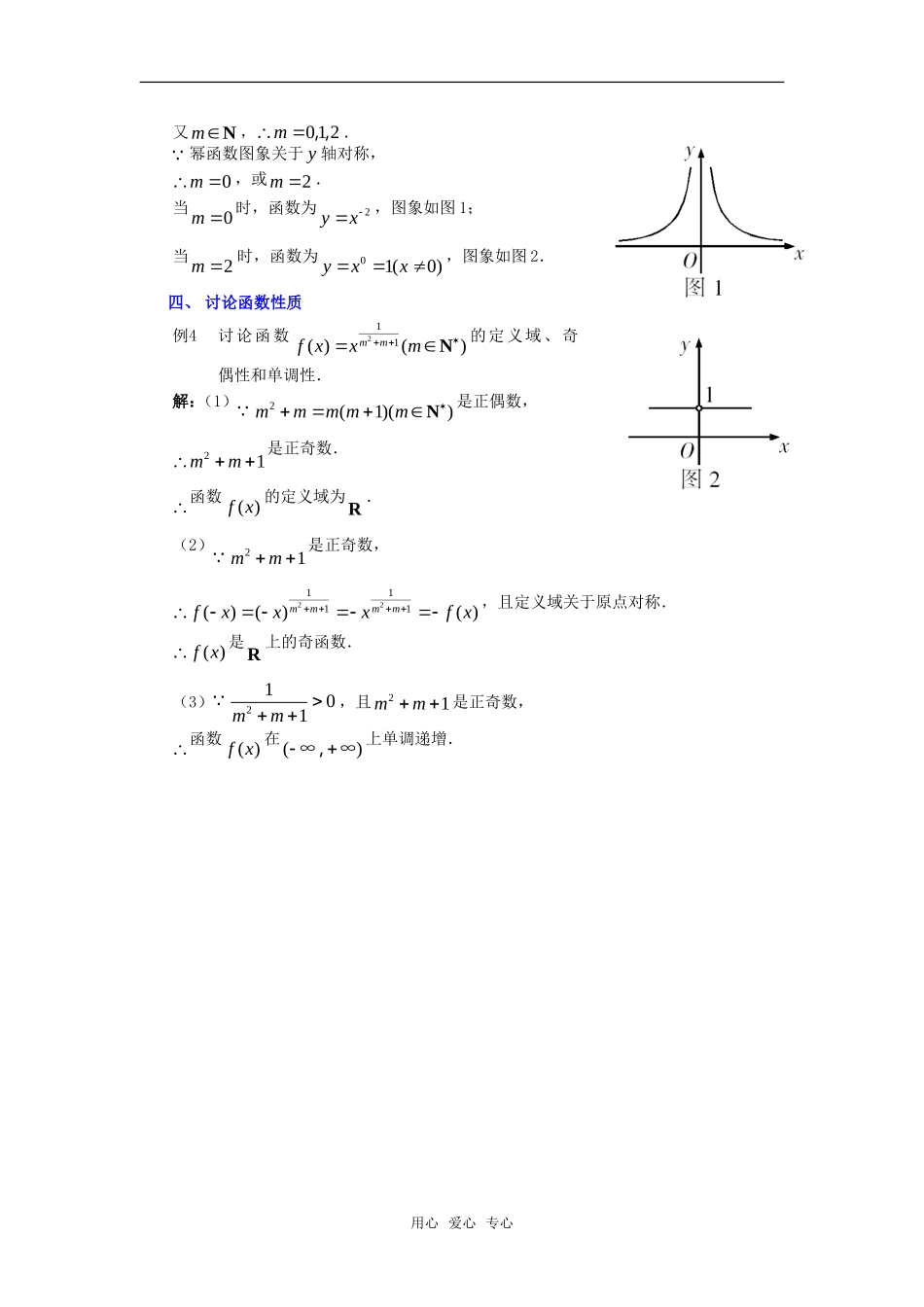
幂函数常见题型例析幂函数是重要的基本初等函数模型之一，下面就其可能出现的题型加以分析，以提高同学们解决问题的能力．一、求解析式例1已知幂函数2223(1)mmymmx，当(0)x，∞时为减函数，则幂函数y．解析：由于2223(1)mmymmx为幂函数，所以211mm，解得2m，或1m．当2m时，2233mm，3yx在(0)，∞上为减函数；当1m时，2230mm，01(0)yxx在(0)，∞上为常函数，不合题意，舍去．故所求幂函数为3yx．点评：求幂函数的解析式，一般用待定系数法，弄明白幂函数的定义是关键．二、比较大小例2比较0.50.8，0.50.9，0.50.9的大小．分析：先利用幂函数0.5yx的增减性比较0.50.8与0.50.9的大小，再根据幂函数的图象比较0.50.9与0.50.9的大小．解：0.5yx在(0)，∞上单调递增，且0.80.9，0.50.50.80.9．作出函数0.5yx与0.5yx在第一象限内的图象，易知0.50.50.90.9．故0.50.50.50.80.90.9．三、求参数的范围例3已知幂函数2()myxmN的图象与xy，轴都无交点，且关于y轴对称，求m的值，并画出它的图象．解：图象与xy，轴都无交点，2m≤0，即2m≤．用心爱心专心又mN，012m，，．幂函数图象关于y轴对称，0m，或2m．当0m时，函数为2yx，图象如图1；当2m时，函数为01(0)yxx，图象如图2．四、讨论函数性质例4讨论函数211()()mmfxxmN的定义域、奇偶性和单调性．解：（1）2(1)()mmmmmN是正偶数，21mm是正奇数．函数()fx的定义域为R．（2）21mm是正奇数，221111()()()mmmmfxxxfx，且定义域关于原点对称．()fx是R上的奇函数．（3）2101mm，且21mm是正奇数，函数()fx在()，∞∞上单调递增．用心爱心专心