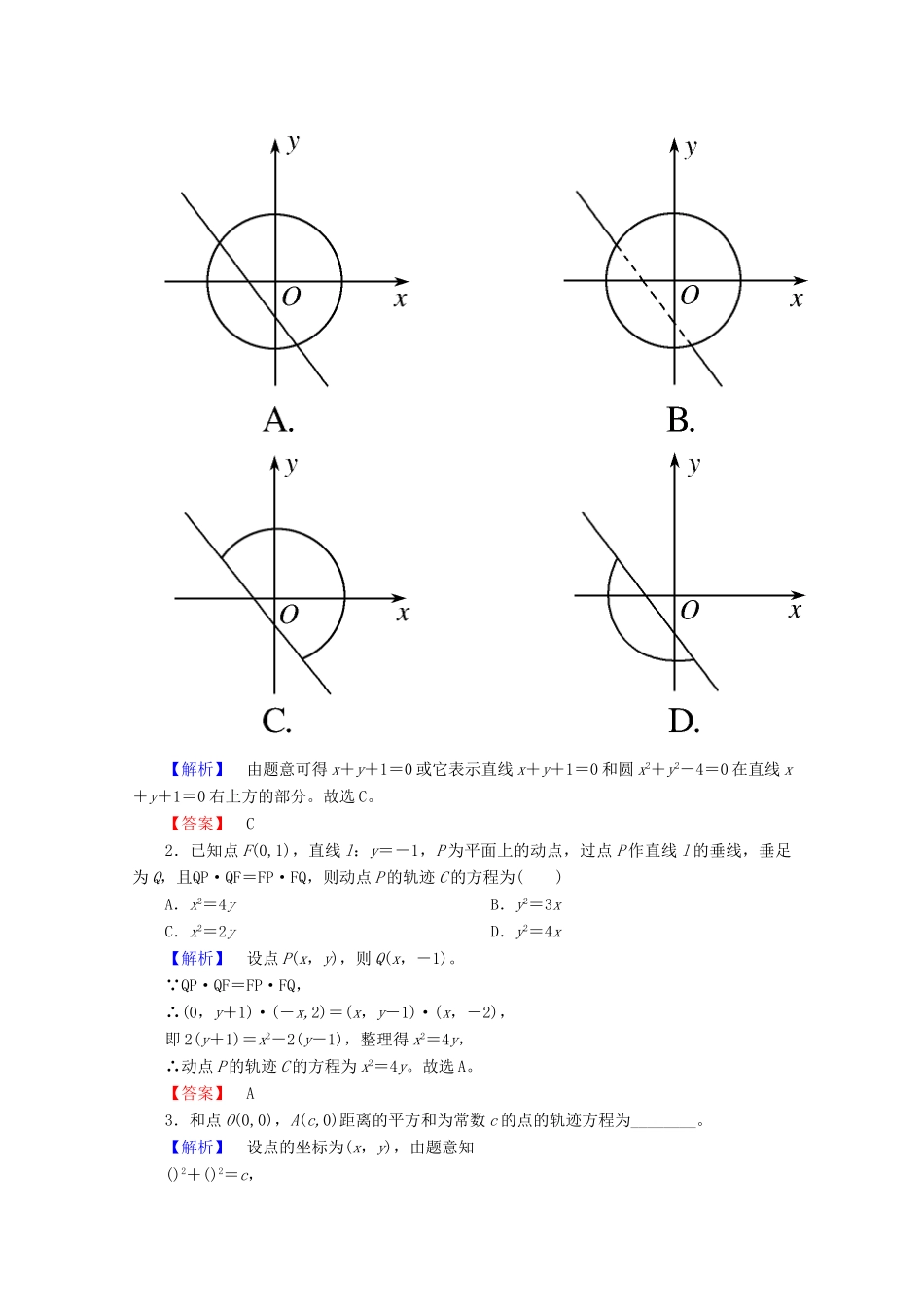
第八节曲线与方程☆☆☆2017考纲考题考情☆☆☆考纲要求真题举例命题角度1.了解方程的曲线与曲线的方程的对应关系;2.了解解析几何的基本思想和利用坐标法研究几何问题的基本方法;3.能够根据所给条件选择适当的方法求曲线的轨迹方程。2016,全国卷Ⅲ,21,12分(求轨迹方程)2015,湖北卷,21(1),5分(求曲线方程)2015,全国卷Ⅰ,20(1),5分(求曲线方程)2013,全国卷Ⅰ,10,5分(求曲线方程)曲线与方程一般在客观题中主要考查圆的方程、椭圆方程、双曲线方程、抛物线方程,以考查待定系数法和定义法为主;在主观题中往往仅作为某一问的形式出现,重点结合圆锥曲线的其他性质进行综合考查。微知识小题练自|主|排|查1.曲线与方程的定义一般地,在直角坐标系中,如果某曲线C上的点与一个二元方程f(x,y)=0的实数解建立了如下的对应关系:(1)曲线C上点的坐标都是这个方程的解;(2)以这个方程的解为坐标的点都是曲线上的点,那么,这个方程叫做曲线的方程,这条曲线叫做方程的曲线。2.求动点的轨迹方程的基本步骤(1)建系:建立适当的平面直角坐标系;(2)设点:轨迹上的任意一点一般设为P(x,y);(3)列式:列出或找出动点P满足的等式;(4)代换:将得到的等式转化为关于x,y的方程;(5)验证:验证所求方程即为所求的轨迹方程。3.曲线的交点与方程组的关系(1)两条曲线交点的坐标是两个曲线方程的公共解,即两个曲线方程组成的方程组的实数解;(2)方程组有几组解,两条曲线就有几个交点;方程组无解,两条曲线就没有交点。微点提醒1.求轨迹方程时,要注意曲线上的点与方程的解是一一对应关系。检验可从以下两个方面进行:一是方程的化简是否是同解变形;二是是否符合题目的实际意义。2.求点的轨迹与轨迹方程是不同的要求,求轨迹时,应先求轨迹方程,然后根据方程说明轨迹的形状、位置、大小等。3.求轨迹问题常用的数学思想(1)函数与方程思想:求平面曲线的轨迹方程就是将几何条件(性质)表示为动点坐标x,y的方程及函数关系。(2)数形结合思想:由曲线的几何性质求曲线方程是“数”与“形”的有机结合。(3)等价转化思想:通过坐标系使“数”与“形”相互结合,在解决问题时又需要相互转化。小|题|快|练一、走进教材1.(必修2P124B组T1改编)等腰三角形ABC,若一腰的两个端点坐标分别是A(4,2),B(-2,0),A是顶点,则另一个点C的轨迹方程为()A.x2+y2-8x-4y=0B.x2+y2-8x-4y-20=0(x≠10,x≠-2)C.x2+y2+8x+4y-20=0(x≠10,x≠-2)D.x2+y2-8x-4y+20=0(x≠10,x≠-2)【解析】设另一个点的坐标为C(x,y),则(x-4)2+(y-2)2=40,x≠10,x≠-2。整理得x2+y2-8x-4y-20=0(x≠10,x≠-2)。故选B。【答案】B2.(选修2-1P36例3改编)若点P到直线x=-1的距离比它到点(2,0)的距离小1,则点P的轨迹为()A.圆B.椭圆C.双曲线D.抛物线【解析】依题意,点P到直线x=-2的距离等于它到点(2,0)的距离,故点P的轨迹是抛物线。故选D。【答案】D二、双基查验1.方程(x2+y2-4)=0的曲线形状是()【解析】由题意可得x+y+1=0或它表示直线x+y+1=0和圆x2+y2-4=0在直线x+y+1=0右上方的部分。故选C。【答案】C2.已知点F(0,1),直线l:y=-1,P为平面上的动点,过点P作直线l的垂线,垂足为Q,且QP·QF=FP·FQ,则动点P的轨迹C的方程为()A.x2=4yB.y2=3xC.x2=2yD.y2=4x【解析】设点P(x,y),则Q(x,-1)。 QP·QF=FP·FQ,∴(0,y+1)·(-x,2)=(x,y-1)·(x,-2),即2(y+1)=x2-2(y-1),整理得x2=4y,∴动点P的轨迹C的方程为x2=4y。故选A。【答案】A3.和点O(0,0),A(c,0)距离的平方和为常数c的点的轨迹方程为________。【解析】设点的坐标为(x,y),由题意知()2+()2=c,即x2+y2+(x-c)2+y2=c,即2x2+2y2-2cx+c2-c=0。【答案】2x2+2y2-2cx+c2-c=04.MA和MB分别是动点M(x,y),与两定点A(-1,0)和B(1,0)的连线,则使∠AMB为直角的动点M的轨迹方程是________。【解析】点M在以A、B为直径的圆上,但不能是A、B两点。【答案】x2+y2=1(x≠±1)5.已知圆的方程为x2+y2=4,若抛物线过点A(-1,0),B(1,0)且以圆的切线为准线,则抛物...