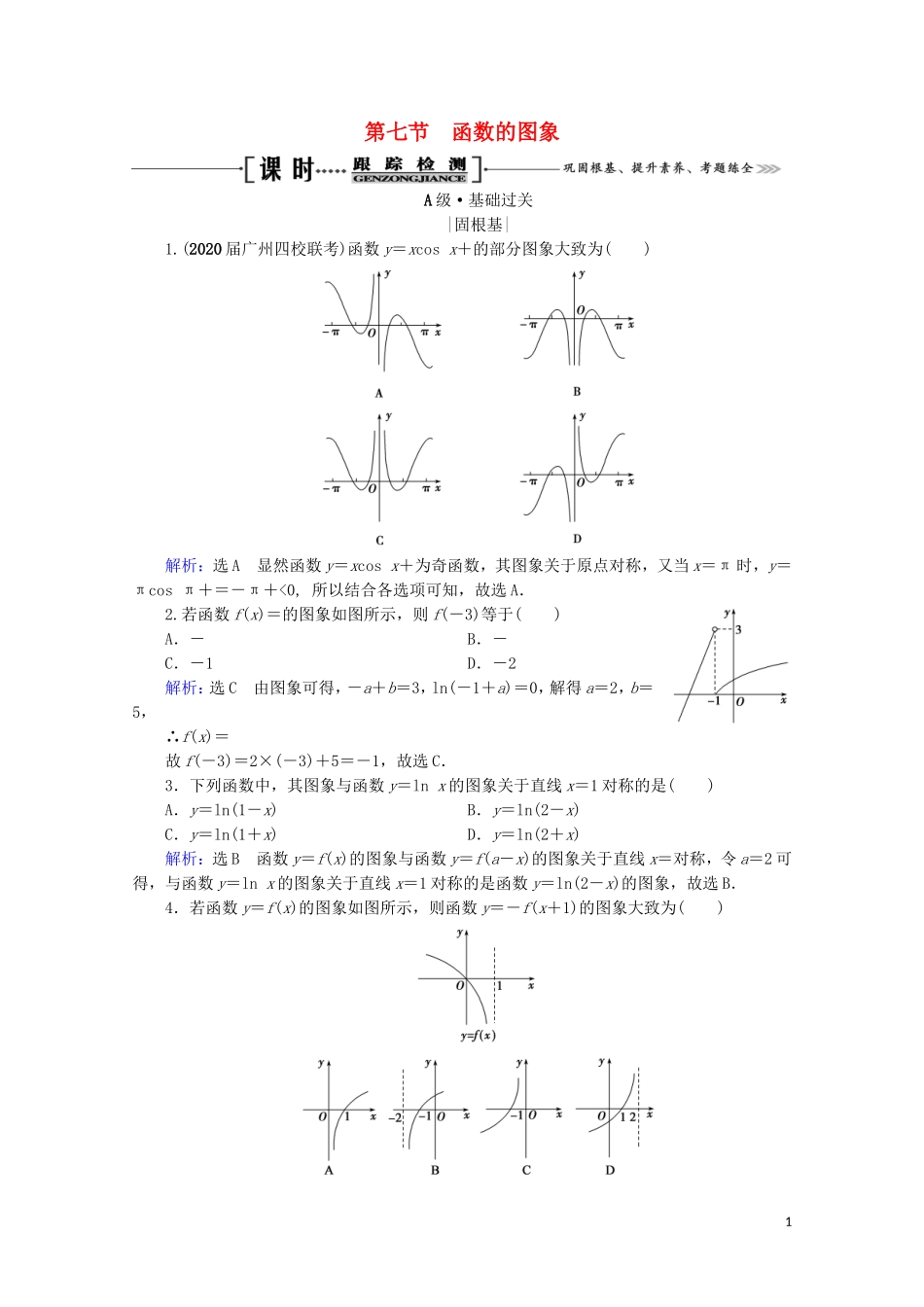
第七节函数的图象A级·基础过关|固根基|1.(2020届广州四校联考)函数y=xcosx+的部分图象大致为()解析:选A显然函数y=xcosx+为奇函数,其图象关于原点对称,又当x=π时,y=πcosπ+=-π+<0,所以结合各选项可知,故选A.2.若函数f(x)=的图象如图所示,则f(-3)等于()A.-B.-C.-1D.-2解析:选C由图象可得,-a+b=3,ln(-1+a)=0,解得a=2,b=5,∴f(x)=故f(-3)=2×(-3)+5=-1,故选C.3.下列函数中,其图象与函数y=lnx的图象关于直线x=1对称的是()A.y=ln(1-x)B.y=ln(2-x)C.y=ln(1+x)D.y=ln(2+x)解析:选B函数y=f(x)的图象与函数y=f(a-x)的图象关于直线x=对称,令a=2可得,与函数y=lnx的图象关于直线x=1对称的是函数y=ln(2-x)的图象,故选B.4.若函数y=f(x)的图象如图所示,则函数y=-f(x+1)的图象大致为()1解析:选C要想由y=f(x)的图象得到y=-f(x+1)的图象,需要先将y=f(x)的图象做关于x轴的对称图象,得到y=-f(x)的图象,然后向左平移一个单位长度得到y=-f(x+1)的图象,故选C.5.(2020届四川五校联考)函数f(x)=tanx-x3的部分图象大致为()解析:选A因为f(-x)=tan(-x)-(-x)3=-tanx+x3=-f(x),故f(x)是奇函数,其图象关于原点对称,排除B、C;f′(x)=-3x2,则f′(0)=1>0,排除D,故选A.6.若函数f(x)=(ax2+bx)ex的图象如图所示,则实数a,b的值可能为()A.a=1,b=2B.a=1,b=-2C.a=-1,b=2D.a=-1,b=-2解析:选B令f(x)=0,则(ax2+bx)ex=0,解得x=0或x=-,由图象可知,->1,又当x>-时,f(x)>0,故a>0,结合选项知,a=1,b=-2满足题意,故选B.7.(2019届昆明检测)已知f(x)=2x-1,g(x)=1-x2,规定当|f(x)|≥g(x)时,h(x)=|f(x)|;当|f(x)|
0时,f(x)=f(x-1),所以f(x)是以1为周期的函数.又当00且a≠1)对于任意的x>2恒成立,则a的取值范围为()A.B.C.[2,+∞)D.(2,+∞)解析:选B不等式4ax-1<3x-4等价于ax-11时,在同一坐标系中作出两个函数的图象,如图1所示,由图知不满足条件;当0