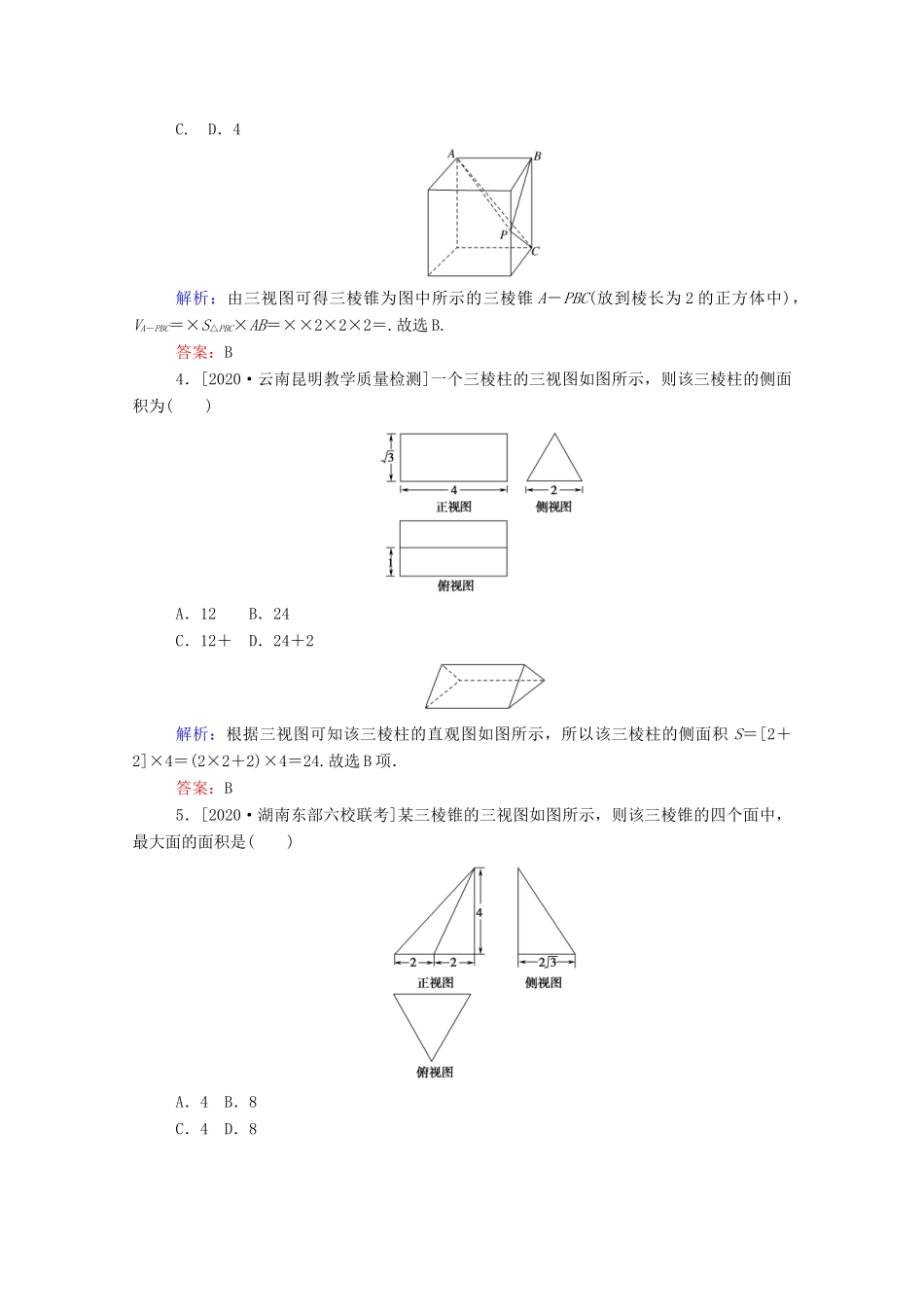
课时作业39空间几何体的表面积和体积[基础达标]一、选择题1.若圆锥的侧面展开图是圆心角为120°,半径为l的扇形,则这个圆锥的表面积与侧面积比是()A.3:2B.2:1C.4:3D.5:3解析:底面半径r=l=l,故圆锥中S侧=πl2,S表=πl2+π2=πl2,所以表面积与侧面积的比为4:3.答案:C2.[2020·重庆一中调考]一个几何体的三视图如图所示,则该几何体的表面积为()A.3πB.4πC.2π+4D.3π+4解析:由几何体的三视图可知,该几何体为半圆柱,直观图如图所示,表面积为2×2+2××π×12+π×1×2=4+3π,故选D项.答案:D3.[2020·益阳市,湘潭市高三调研]如图,网格纸上小正方体的边长为1,粗实线画出的是某三棱锥的三视图,则该三棱锥的体积是()A.B.C.D.4解析:由三视图可得三棱锥为图中所示的三棱锥A-PBC(放到棱长为2的正方体中),VA-PBC=×S△PBC×AB=××2×2×2=.故选B.答案:B4.[2020·云南昆明教学质量检测]一个三棱柱的三视图如图所示,则该三棱柱的侧面积为()A.12B.24C.12+D.24+2解析:根据三视图可知该三棱柱的直观图如图所示,所以该三棱柱的侧面积S=[2+2]×4=(2×2+2)×4=24.故选B项.答案:B5.[2020·湖南东部六校联考]某三棱锥的三视图如图所示,则该三棱锥的四个面中,最大面的面积是()A.4B.8C.4D.8解析:如图,设该三棱锥为P-ABC,其中PA⊥底面ABC,PA=4,△ABC是边长为4的等边三角形,故PB=PC=4,所以S△ABC=×4×2=4,S△PAB=S△PAC=×4×4=8,S△PBC=×4×=4,故四个面中最大面的面积为S△PBC=4,故选C项.答案:C6.[2020·湖南六校联考]如图是一个几何体的三视图,且这个几何体的体积为8,则x等于()A.1B.2C.3D.4解析:由三视图可知,该几何体为一个底面是直角梯形的四棱锥(如图),体积V=·x=8,∴x=4.故选D项.答案:D7.[2020·山东德州联考]圆锥被一个平面截去一部分后与半球组成一个几何体,如图所示是该几何体的三视图,则该几何体的表面积为()A.5π+4B.10π+4C.14π+4D.18π+4解析:由三视图可知该几何体是由半个圆锥和半个球构成的,所以几何体的表面积为×4×2+×π×22+×4×π×22+×2π×=14π+4.故选C项.答案:C8.[2020·北京昌平区检测]《九章算术》是我国古代数学著作,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:在屋内墙角处堆放米,米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积及堆放的米各为多少?已知米堆所形成的几何体的三视图如图所示,一斛米的体积约为1.62立方尺,由此估算出堆放的米约有()A.21斛B.34斛C.55斛D.63斛解析:设圆锥的底面圆的半径为r,则r=8,解得r=,故米堆的体积为××π×()2×5=(立方尺). 1斛米的体积约为1.62立方尺,∴÷1.62≈21(斛),故选A项.答案:A9.[2019·河南新乡二模]已知一个几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.解析:由三视图可知,该几何体由一个三棱锥和一个三棱柱组合而成,其直观图如图所示,结合三视图中的数据可知该几何体的体积V=V柱+V锥=×(1+1)×1×2+××(1+1)×1×2=,故选C项.答案:C10.[2020·广东深圳调研]如图,在平面四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD,将其沿对角线BD折成四面体ABCD,使平面ABD⊥平面BCD,若四面体ABCD的所有顶点在同一个球面上,则该球的体积为()A.B.3πC.D.2π解析:如图,取BD的中点E,BC的中点O,连接AE,OD,EO,AO.因为AB=AD,所以AE⊥BD.由于平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,所以AE⊥平面BCD.因为AB=AD=CD=1,BD=,所以AE=,EO=,所以OA=.在Rt△BDC中,OB=OC=OD=BC=,所以四面体ABCD的外接球的球心为O,半径为,所以该球的体积V=π×()3=.答案:A二、填空题11.[2020·南昌模拟]如图,直角梯形ABCD中,AD⊥DC,AD∥BC,BC=2CD=2AD=2,若将直角梯形绕BC边旋转一周,则所得几何体的表面积为________.解析:本题考查几何体的表面积.所得几何体的表面积是底面圆半径为1、高为1的圆柱的下底面积、侧面积和底面圆半径为1、高为1的圆锥的侧面积之和,即为π+2π...