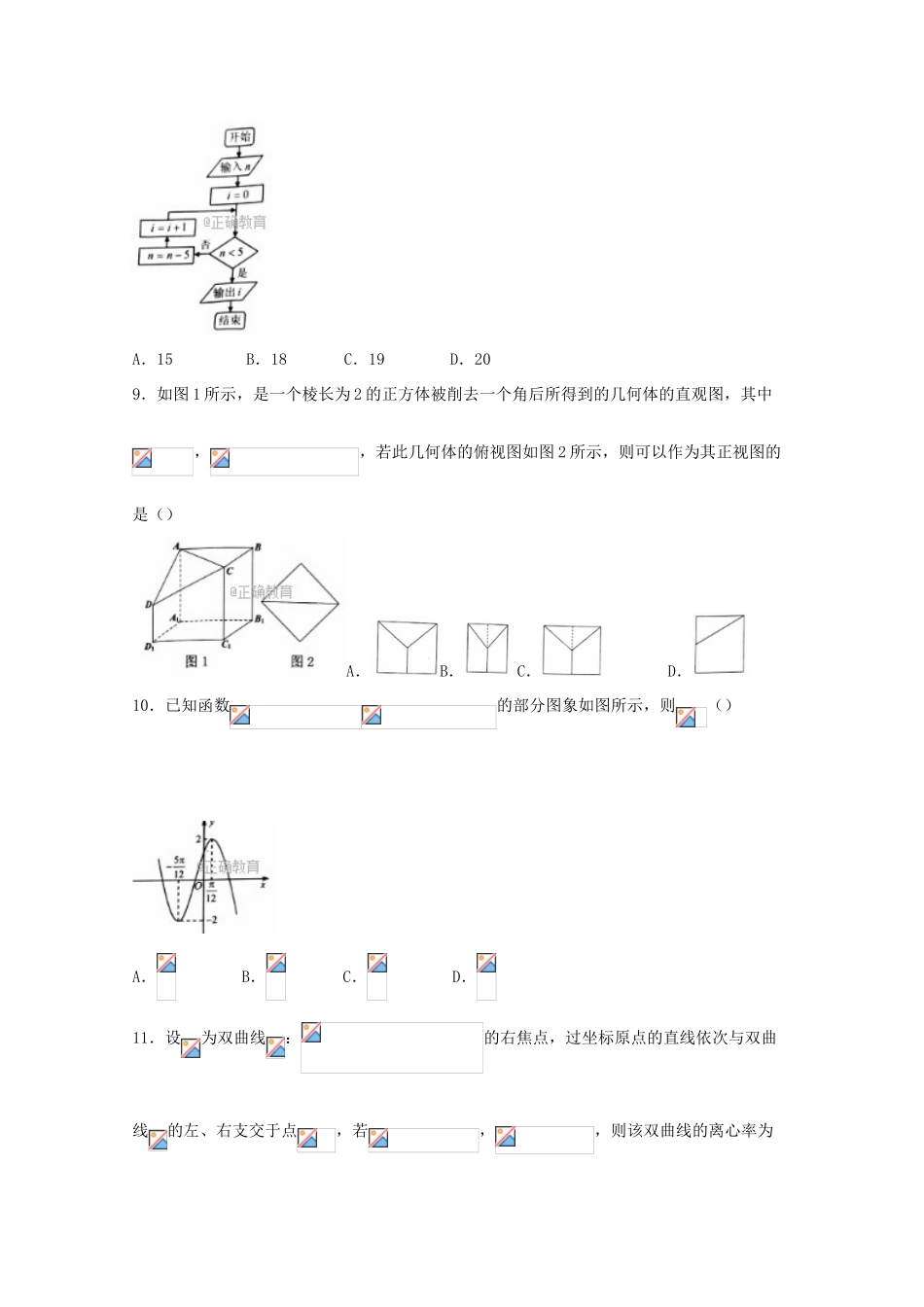
2018届高三摸底考试文科数学试卷一、选择题:1.设集合,,则()A.B.C.D.2.若复数满足,其中为虚数单位,则在复平面内所对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.已知向量,,若,则()A.B.C.2D.44.在平面直角坐标系中,不等式组所表示的平面区域的面积为()A.B.C.D.5.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今共织九十尺,问织几日?”,已知“日减功迟”的具体含义是每天比前一天少织同样多的布,则此问题的答案是()A.10日B.20日C.30日D.40日6.设直线与圆相交于两点,为坐标原点,若为等边三角形,则实数的值为()A.B.C.D.7.方程表示双曲线的一个充分不必要条件是()A.B.C.D.8.执行如图所示的程序框图,若输出的结果为3,则输入的数不可能是()A.15B.18C.19D.209.如图1所示,是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图,其中,,若此几何体的俯视图如图2所示,则可以作为其正视图的是()A.B.C.D.10.已知函数的部分图象如图所示,则()A.B.C.D.11.设为双曲线:的右焦点,过坐标原点的直线依次与双曲线的左、右支交于点,若,,则该双曲线的离心率为()A.B.C.D.12.已知函数,设关于的方程有个不同的实数解,则的所有可能的值为()A.3B.1或3C.4或6D.3或4或6二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若关于的不等式的解集为,则.14.设中,角所对的边分别为,若的面积为,则.15.甲、乙两组数据的茎叶图如图所示,其中为小于10的自然数,已知甲组数据的中位数大于乙组数据的中位数,则甲组数据的平均数也大于乙组数据的平均数的概率为.16.设函数,若在区间上的值域为,则实数的取值范围为.三、解答题17.已知等差数列的前项和为,,.(1)求;(2)设数列的前项和为,证明:.18.“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?附:,0.100.050.0250.0102.7063.8415.0246.63519.如图,矩形中,,,为的中点,将沿折到的位置,.(1)求证:平面平面;(2)若为的中点,求三棱锥的体积.20.已知椭圆:的左顶点为,右焦点为,过点且斜率为1的直线交椭圆于另一点,交轴于点,.(1)求椭圆的方程;(2)过点作直线与椭圆交于两点,连接(为坐标原点)并延长交椭圆于点,求面积的最大值及取最大值时直线的方程.21.已知函数,.(1)分别求函数与在区间上的极值;(2)求证:对任意,.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在直角坐标系中,直线的参数方程为(为参数),以坐标原点为极点,以轴正半轴为极轴,建立极坐标系,曲线的极坐标方程为.(1)写出曲线的直角坐标方程;(2)已知点的直角坐标为,直线与曲线相交于不同的两点,求的取值范围.23.选修4-5:不等式选讲已知函数.(1)若的最小值为2,求的值;(2)若对,,使得不等式成立,求实数的取值范潮南实验学校2018届高三摸底考试文科数学试卷试卷答案一、选择题1~6DCCBBC7~12AAABBB第(11)题解析:,,设双曲线的左焦点为,连接,由对称性可知,为矩形,且,故.第(12)题解析:,在和上单增,上单减,又当时,时,故的图象大致为:令,则方程必有两根且,当时恰有,此时有1个根,有2个根;当时必有,此时无根,有3个根;当时必有,此时有2个根,有1个根;综上,对任意,方程均有3个根.二、填空题(13)(14)(15)(16)第(15)题解析:由甲的中位数大于乙的中位数知,,又由甲的平均数大于乙的平均数知,即,...