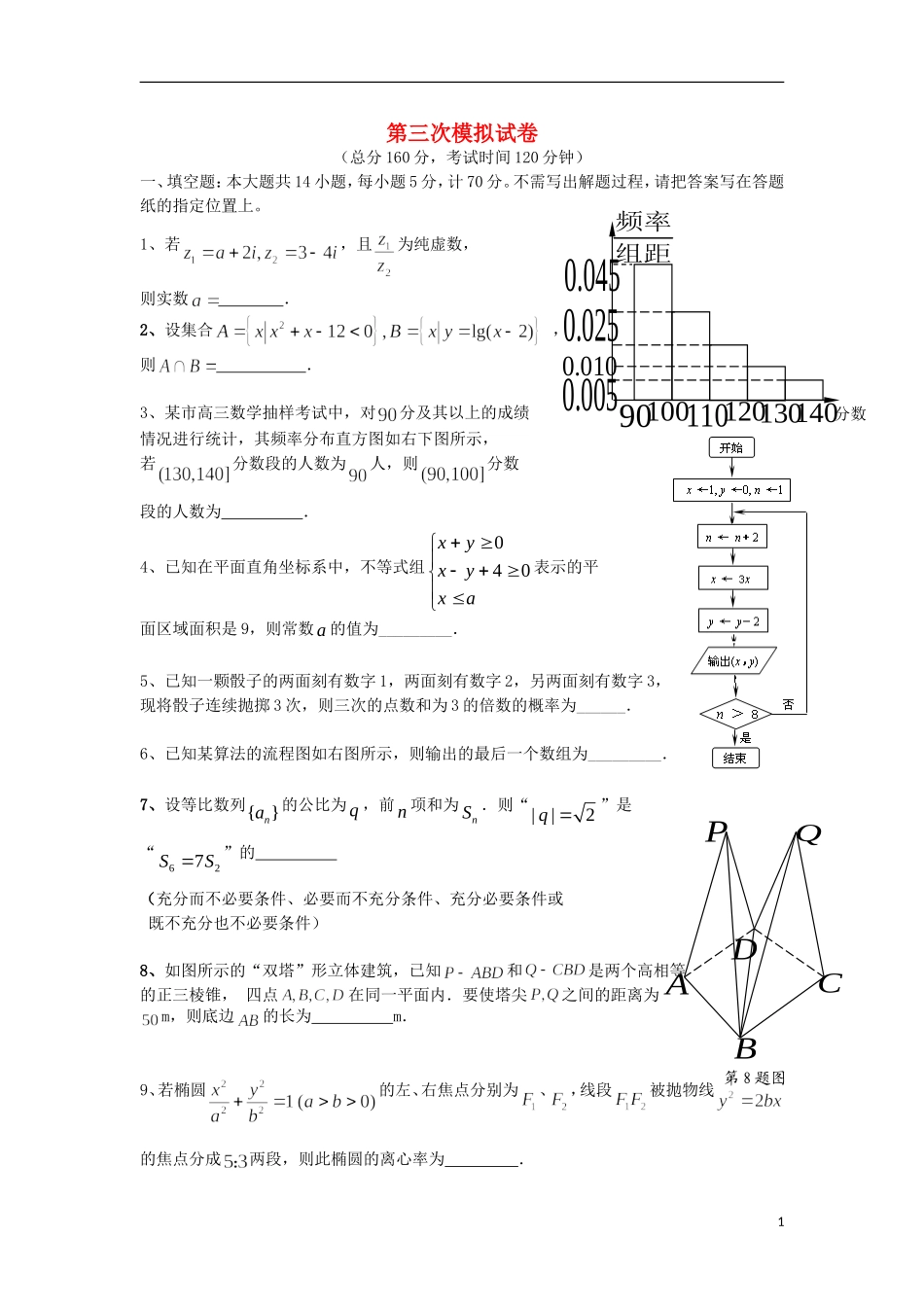
第三次模拟试卷(总分160分,考试时间120分钟)一、填空题:本大题共14小题,每小题5分,计70分。不需写出解题过程,请把答案写在答题纸的指定位置上。1、若,且为纯虚数,则实数.2、设集合,则.3、某市高三数学抽样考试中,对分及其以上的成绩情况进行统计,其频率分布直方图如右下图所示,若分数段的人数为人,则分数段的人数为.4、已知在平面直角坐标系中,不等式组axyxyx040表示的平面区域面积是9,则常数a的值为_________.5、已知一颗骰子的两面刻有数字1,两面刻有数字2,另两面刻有数字3,现将骰子连续抛掷3次,则三次的点数和为3的倍数的概率为______.6、已知某算法的流程图如右图所示,则输出的最后一个数组为_________.7、设等比数列{}na的公比为q,前n项和为nS.则“||2q”是“627SS”的(充分而不必要条件、必要而不充分条件、充分必要条件或既不充分也不必要条件)8、如图所示的“双塔”形立体建筑,已知和是两个高相等的正三棱锥,四点在同一平面内.要使塔尖之间的距离为m,则底边的长为m.9、若椭圆的左、右焦点分别为、,线段被抛物线的焦点分成两段,则此椭圆的离心率为.1分数频率组距901001101201301400.0050.0100.0250.045PQABCD第8题图NMEDCBA10、若实数、满足,则的最大值是▲.11.已知直线x=a(0<a<)与函数f(x)=sinx和函数g(x)=cosx的图象分别交于M,N两点,若MN=,则线段MN的中点纵坐标为▲.12、设是定义在上的奇函数,且当时,,若对任意的不等式恒成立,则的最大值为▲13.如图,两射线,AMAN互相垂直,在射线AN上取一点B使AB的长为定值2a,在射线AN的左侧以AB为斜边作一等腰直角三角形ABC.在射线,AMAN上各有一个动点,DE满足ADE与ABC的面积之比为3:2,则CDED�的取值范围为____________.14.已知定义在上的函数和满足,,.令,则使数列的前项和超过15/16的最小自然数的值为.二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)已知锐角中的三个内角分别为.⑴设,求证是等腰三角形;⑵设向量,,且∥,若,求的值.16.(本小题满分14分)在直三棱柱中,AC=4,CB=2,AA1=2,,E、F分别是的中点.(1)证明:平面平面;(2)证明:平面ABE;(3)设P是BE的中点,求三棱锥的体积.2ABCEFP1A1B1C17.(本题满分14分)如图,有一块边长为1(百米)的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角PAQ始终为45(其中点P、Q分别在边BC、CD上),设,tanPABt,探照灯照射在正方形ABCD内部区域的面积S(平方百米)。(1)将S表示成t的函数;(2)求S的最大值。18.(本题满分16分)已知椭圆的中心在原点,长轴在x轴上,右顶点到右焦点的距离与它到右准线的距离之比为.不过A点的动直线交椭圆于P,Q两点.(1)求椭圆的标准方程;(2)证明P,Q两点的横坐标的平方和为定值;(3)过点A,P,Q的动圆记为圆C,动圆C过不同于A的定点,请求出该定点坐标.19.(本小题满分16分)已知函数(1)当时,求的单调区间(2)设,当时,若对任意,存在,使3,求实数的取值范围.20.(本小题满分16分)对于项数为m的有穷数列数集}{na,记},,,max{21kkaaab(k=1,2,…,m),即kb为kaaa,,,21中的最大值,并称数列}{nb是}{na的控制数列.如1,3,2,5,5的控制数列是1,3,3,5,5.(1)若各项均为正整数的数列}{na的控制数列为2,3,4,5,5,写出所有的}{na;(2)设}{nb是}{na的控制数列,满足Cbakmk1(C为常数,k=1,2,…,m).求证:kkab(k=1,2,…,m);(3)设m=100,常数)1,(21a.若nanannn2)1()1(2,}{nb是}{na的控制数列,求)()()(1001002211ababab.4