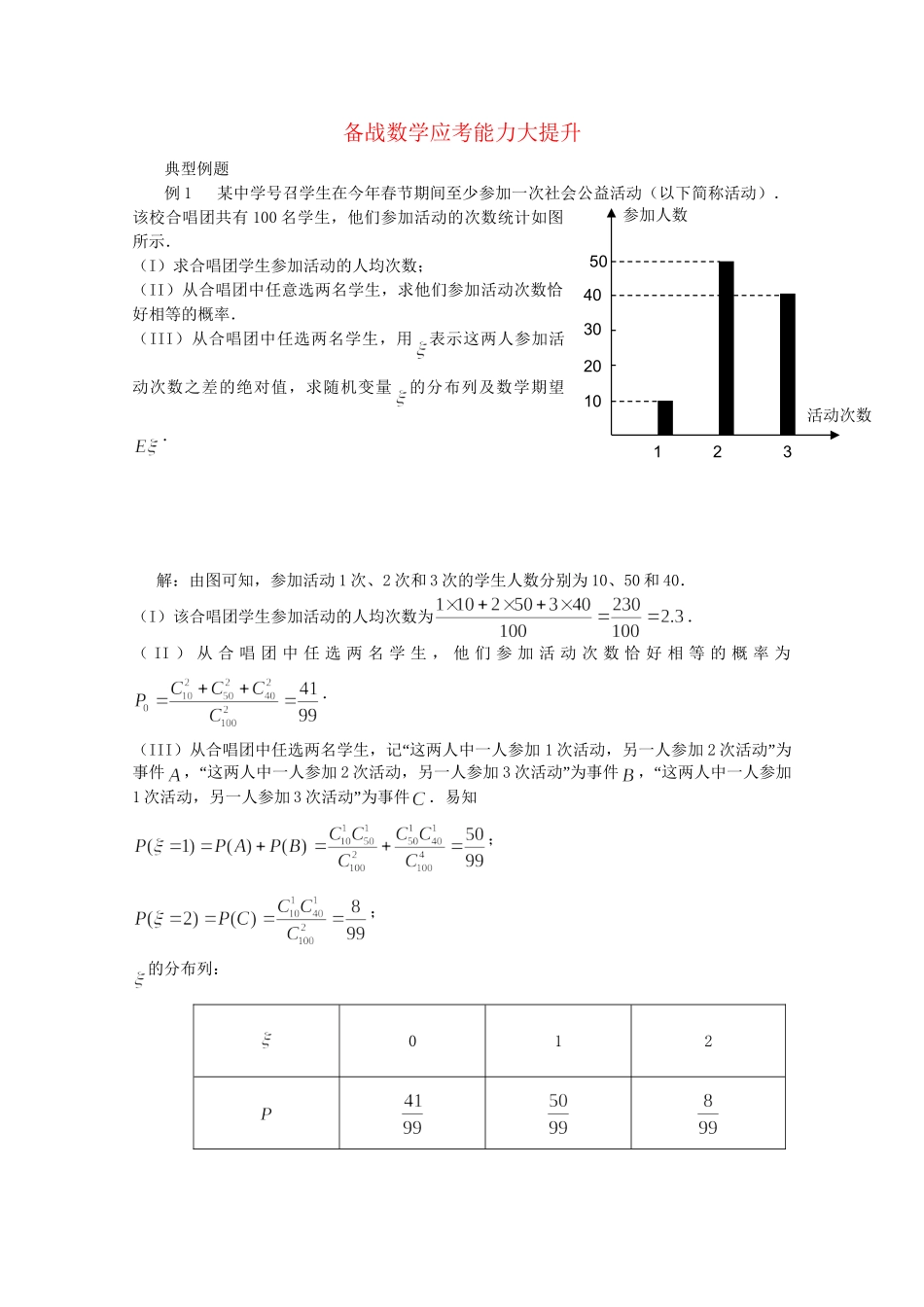
备战数学应考能力大提升典型例题例1某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.(I)求合唱团学生参加活动的人均次数;(II)从合唱团中任意选两名学生,求他们参加活动次数恰好相等的概率.(III)从合唱团中任选两名学生,用表示这两人参加活动次数之差的绝对值,求随机变量的分布列及数学期望.解:由图可知,参加活动1次、2次和3次的学生人数分别为10、50和40.(I)该合唱团学生参加活动的人均次数为.(II)从合唱团中任选两名学生,他们参加活动次数恰好相等的概率为.(III“)从合唱团中任选两名学生,记这两人中一人参加1次活动,另一人参加2”次活动为事件“,这两人中一人参加2次活动,另一人参加3”次活动为事件“,这两人中一人参加1次活动,另一人参加3”次活动为事件.易知;;的分布列:0121231020304050参加人数活动次数的数学期望:.例2在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:(l)第1次抽到理科题的概率;(2)第1次和第2次都抽到理科题的概率;(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.解:设第1次抽到理科题为事件A,第2次抽到理科题为事件B,则第1次和第2次都抽到理科题为事件AB.(1)从5道题中不放回地依次抽取2道的事件数为n()==20.根据分步乘法计数原理,n(A)==12.于是.(2)因为n(AB)==6,所以.(3)解法1由(1)(2)可得,在第1次抽到理科题的条件下,第2次抽到理科题的概.解法2因为n(AB)=6,n(A)=12,所以.创新题型1.将一颗骰子先后抛掷两次,得到的点数分别记为a、b.(1)求点P(a,b)落在区域内的概率;(2)求直线ax+by+5=0与圆x2+y2=1不相切的概率.2.一张储蓄卡的密码共有6位数字,每位数字都可以从0~9中任选一个。某人在银行自动提款机上取钱时,忘记了密码的最后一位数字。求:(1)任意按最后一位数字,不超过2次就按对的概率。(2)如果他记得密码的最后一位是偶数,不超过2次就按对的概率。参考答案1.【解析】(1)先后两次抛掷一枚骰子,将得到的点数分别记为a,b,则事件总数为6×6=36.∴表示的平面区域如图所示:当a=1时,b=1,2,3,4a=2时,b=1,2,3a=3时,b=1,2a=4时,b=1共有(1,1),(1,2)…,,(4,1)10种情况,∴P==.(2)∵直线ax+by+5=0与圆x2+y2=1相切的充要条件是=1,即a2+b2=25,∵a、b∈{1,2,3,4,5,6},满足条件的情况只有:a=3,b=4或a=4,b=3两种情况,∴直线与圆相切的概率P==.∴直线ax+by+5=0与圆x2+y2=1不相切的概率P=1-=.2解:设第i次按对密码为事件(i=1,2),则表示不超过2次就按对密码.(1)因为事件与事件互斥,由概率的加法公式得