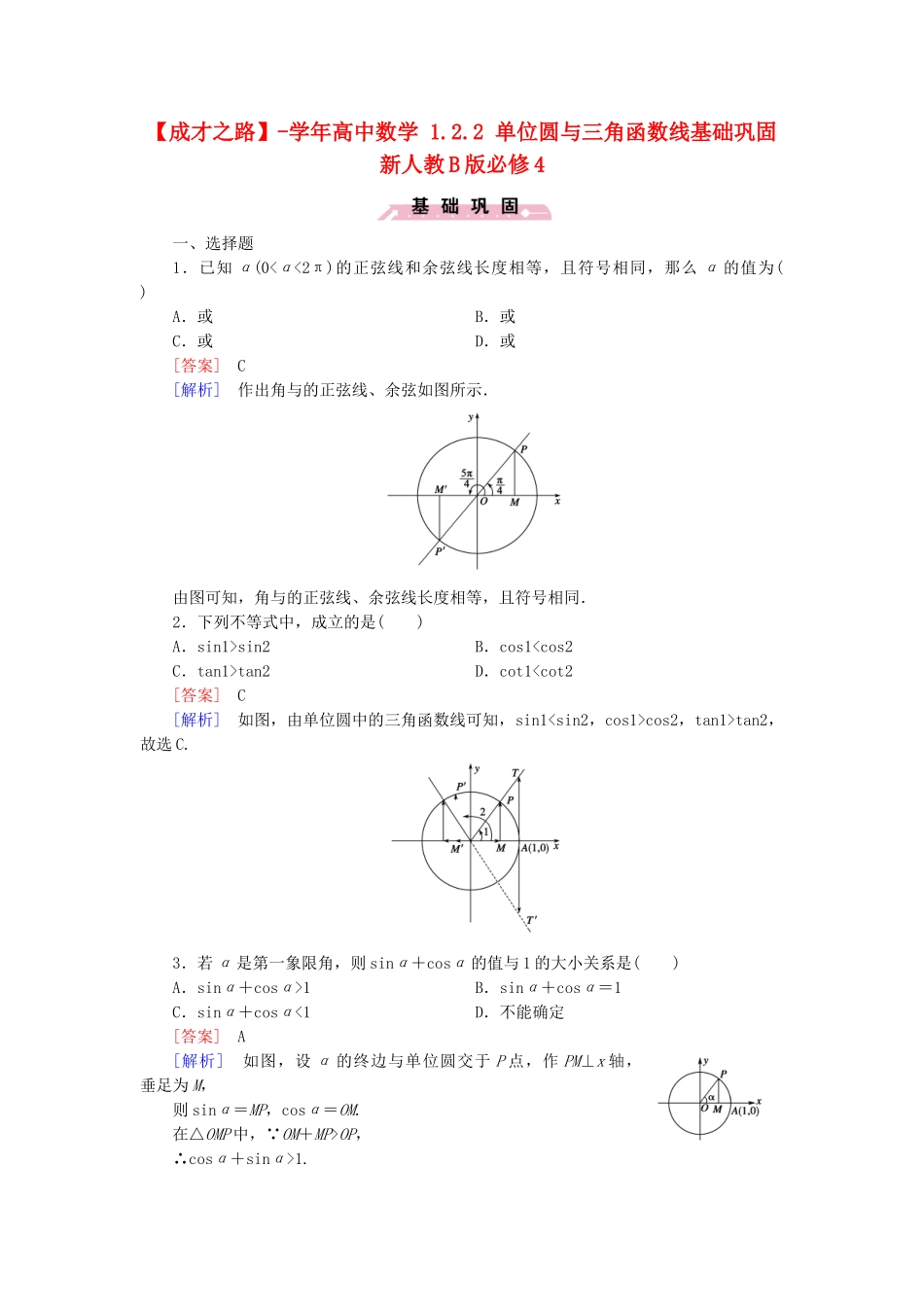
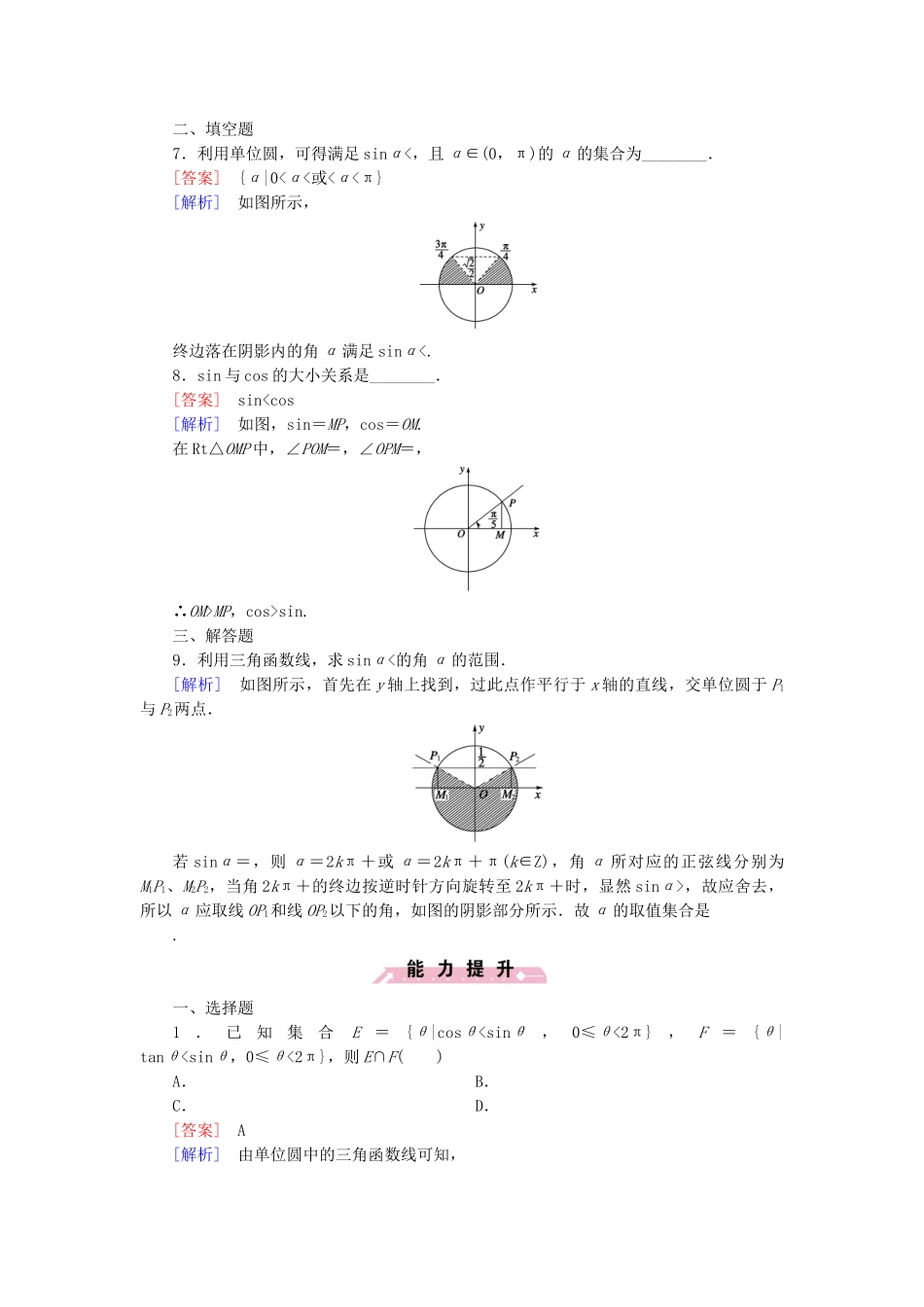
【成才之路】-学年高中数学1.2.2单位圆与三角函数线基础巩固新人教B版必修4一、选择题1.已知α(0<α<2π)的正弦线和余弦线长度相等,且符号相同,那么α的值为()A.或B.或C.或D.或[答案]C[解析]作出角与的正弦线、余弦如图所示.由图可知,角与的正弦线、余弦线长度相等,且符号相同.2.下列不等式中,成立的是()A.sin1>sin2B.cos1tan2D.cot1cos2,tan1>tan2,故选C.3.若α是第一象限角,则sinα+cosα的值与1的大小关系是()A.sinα+cosα>1B.sinα+cosα=1C.sinα+cosα<1D.不能确定[答案]A[解析]如图,设α的终边与单位圆交于P点,作PM⊥x轴,垂足为M,则sinα=MP,cosα=OM.在△OMP中,∵OM+MP>OP,∴cosα+sinα>1.4.(·济南一中高一月考)使sinx≤cosx成立的x的一个区间是()A.[-,]B.[-,]C.[-,]D.[0,π][答案]A[解析]如图阴影部分满足sinx≤cosx,故选A.5.已知点P(sinα-cosα,tanα)在第一象限,则在[0,2π)内的角α的取值范围是()A.∪B.∪C.∪D.∪[答案]B[解析]∵点P(sinα-cosα,tanα)在第一象限,∴,即由②知α在第一、三象限.由①sinα>cosα,用正弦线、余弦线得出图中的阴影部分满足.故α的取值范围是:∪,故选B.6.已知α是第三象限角,则下列等式中可能成立的是()A.sinα+cosα=1.2B.sinα+cosα=-0.9C.sinαcosα=D.sinα+cosα=-1.2[答案]D[解析]如图,由三角函数线知,sinα=MP,cosα=OM,sinα+cosα=MP+OM,|MP|+|OM|>|OP|=1,又MP<0,OM<0,∴MP+OM<-1,故选D.二、填空题7.利用单位圆,可得满足sinα<,且α∈(0,π)的α的集合为________.[答案]{α|0<α<或<α<π}[解析]如图所示,终边落在阴影内的角α满足sinα<.8.sin与cos的大小关系是________.[答案]sinMP,cos>sin.三、解答题9.利用三角函数线,求sinα<的角α的范围.[解析]如图所示,首先在y轴上找到,过此点作平行于x轴的直线,交单位圆于P1与P2两点.若sinα=,则α=2kπ+或α=2kπ+π(k∈Z),角α所对应的正弦线分别为M1P1、M2P2,当角2kπ+的终边按逆时针方向旋转至2kπ+时,显然sinα>,故应舍去,所以α应取线OP1和线OP2以下的角,如图的阴影部分所示.故α的取值集合是.一、选择题1.已知集合E={θ|cosθcosβ,则sinα>sinβB.α、β都是第二象限角,若sinα>sinβ,则tanα>tanβC.α、β都是第三象限角,若cosα>cosβ,则sinα>sinβD.α、β都是第四象限角,若sinα>sinβ,则tanα>tanβ[答案]D[解析]如图,α、β都是第一象限角,cosα>cosβ,则sinαsinβ,则tanαcosβ,则sinα1,若α是第三象限角,则sinα+cosα<-1,若sinα+cosα=,则α是第二或四象限角.三、解答题5.确定下式的符号:sin1-cos1.[分析]在单位圆中作出1,的正弦线、余弦线,将sin1、cos1与sin比较即可.[解析]因为<1<,如图所示,由三角函数线可得sin1>>cos1,故sin1-cos1>0.6.求满足下列条件的角x的集合:(1)已知tanx>0,且sinx+cosx>0;(2)已知tanx<0,且sinx-cosx<0.[解析](1){x|2kπ