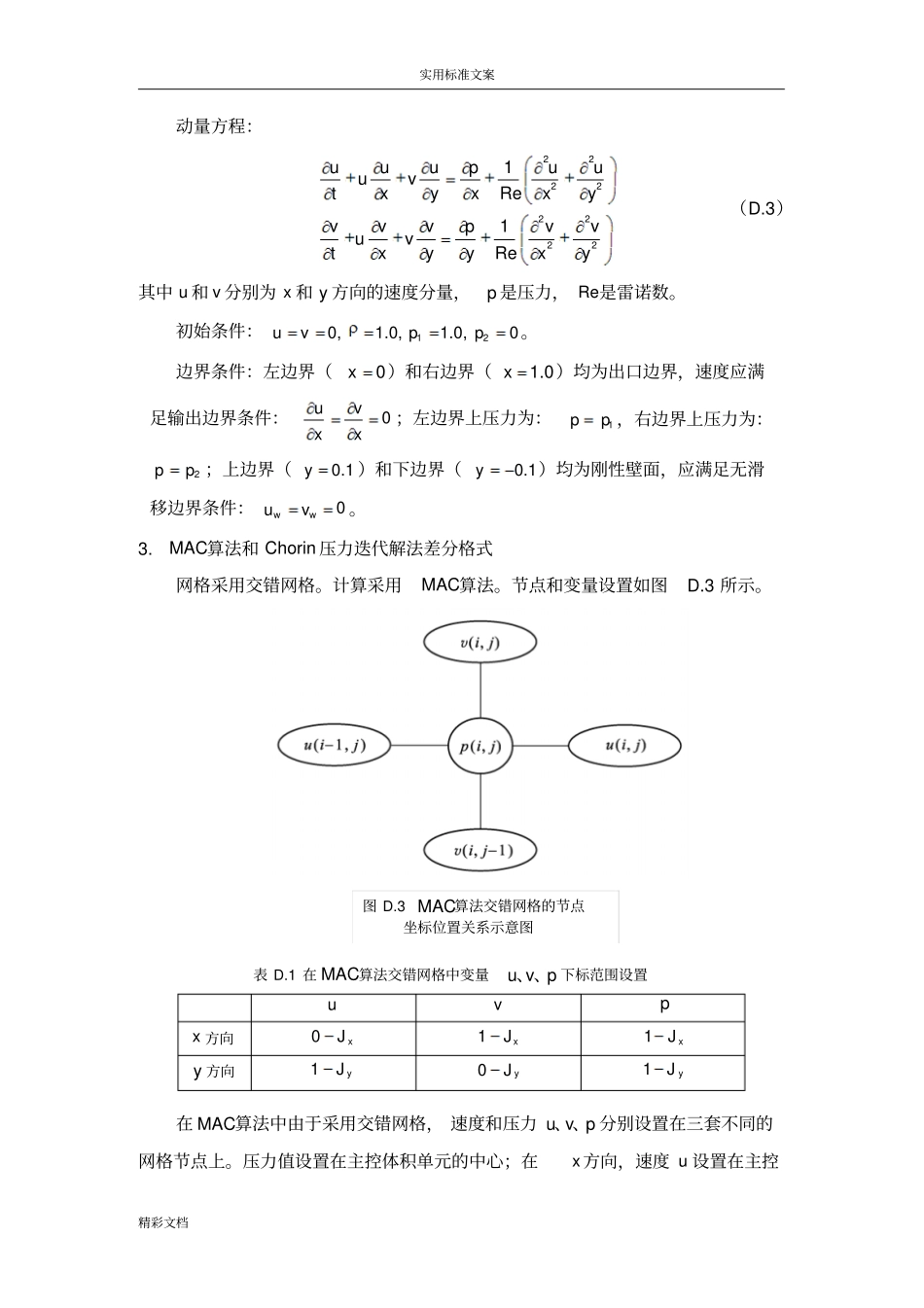
实用标准文案精彩文档附录D二维不可压缩黏性流体Poisuille流动问题的数值解与计算程序二维Poisuille流动问题是有解析解的二维不可压缩黏性流动。对它采用MAC算法和Chorin压力迭代解法进行数值求解。同时,为了初学者入门和练习方便,这里给出了由C语言和Fortran77语言编写的计算二维不可压缩黏性流体Poisuille流动问题的计算程序,供大家学习参考。D-1MAC算法和Chorin压力迭代解法求解二维不可压缩黏性Poisuille流动问题1.二维不可压缩黏性流体Poisuille流动问题设在水平方向上有两块无限长固定不动的平行平板,它们的间距为2h,两平板间充满不可压缩黏性流体。平板间两个横截面11和22上压力分别为1p和2p,当1p和2p不同时,平板间不可压缩黏性流体就会产生流动,并在平板间形成一个速度分布剖面,这就是著名的二维不可压缩黏性流体Poisuille流动问题,如图D.1和图D.2所示。假定忽略质量力,且认为流动是定常层流。在平板间的横截面上黏性流体的速度分布精确解为:22122ppuhyl(D.1)2.基本方程组、初始条件和边界条件二维Poisuille流动问题在数学上可以用二维不可压缩黏性流动N-S方程组来描述:连续方程:0uvDxy(D.2)图D.1二维Poisuille流动示意图图D.2二维Poisuille流动横截面速度分布示意图实用标准文案精彩文档动量方程:2222222211uuupuuuvtxyxRexyvvvpvvuvtxyyRexy(D.3)其中u和v分别为x和y方向的速度分量,p是压力,Re是雷诺数。初始条件:120,1.0,1.0,0uvpp。边界条件:左边界(0x)和右边界(1.0x)均为出口边界,速度应满足输出边界条件:0uvxx;左边界上压力为:1pp,右边界上压力为:2pp;上边界(0.1y)和下边界(0.1y)均为刚性壁面,应满足无滑移边界条件:0wwuv。3.MAC算法和Chorin压力迭代解法差分格式网格采用交错网格。计算采用MAC算法。节点和变量设置如图D.3所示。表D.1在MAC算法交错网格中变量uvp、、下标范围设置uvpx方向0xJ1xJ1xJy方向1yJ0yJ1yJ在MAC算法中由于采用交错网格,速度和压力uvp、、分别设置在三套不同的网格节点上。压力值设置在主控体积单元的中心;在x方向,速度u设置在主控图D.3MAC算法交错网格的节点坐标位置关系示意图实用标准文案精彩文档体积单元东、西两个侧面的辅助体积单元上,而在y方向,速度v设置在主控体积单元南、北两个侧面的辅助体积单元上。为了便于处理u和v的边界条件,在边界四周加设一层虚拟网格。三个变量uvp、、的下标范围如表D.1所示:对方程(D.3)中对流项和扩散项采用中心差分格式。动量方程中u的差分格式为:1,,nnijijuuADVXPRSXVISX(D.4)其中,1,1,,,11,1,1,1,11,,1,,1,,1,,12228221nnnnnnnnnijijijijijijijijijnnijijnnnnnnijijijijijijuuuvvvvuuADVXxyppPRSXxuuuuuuVISXRexy(D.5)动量方程中v的差分格式为:1,,nnijijvvADVYPRSYVISY(D.6)其中1,,1,1,11,1,,,1,1,1,11,,1,,1,,12282221nnnnnnnnnijijijijijijijijijnnijijnnnnnnijijijijijijuuuuvvuvvADVYxyppPRSYyvvvvvvVISYRexy(D.7)压力差分格式为:1,,nnijijppCONV(D.8)其中1111,1,,,1nnnnijijijijuuvvCONVxy(D.9)当在所有网格点中满足下面条件时,则可得到定常解:1111,1,,,1||nnnnijijijijuuvvCONVxy(D.10)式中是一小量,一般取410。压力和速度之间迭代过程采用Chorin压力迭代解法。具体迭代过程如下:首实用标准文案精彩文档先由式(D.1)差分格式计算出1,()nmijD值[当m=1时,11,2niju、11,2nijv用1,2niju、1,2nijv值来代替,求出1,()nmijD值,其中m为迭代次数];然后利用压力修正公式:1111,,,mmmnnnijijijppD(D.11)求出11,mnijp[当m=1时,1,nijp用,nijp值来代替,计算出11,mnijp值],其中是松弛因子,必须满足如下稳定性条件:22111txy(D.12)为了减少迭代次数,通常可取最佳值max0.9opt;最后利用动量方程u、v差分格式求出11,2niju和11,2nijv值,并利用散度差分格式,重新计算1,nijD,检验散度是否满足1,nijD,如果不满足,则需要重复计算,直到收敛。4.计算结果分析计算分别采用标准的C语言和Fortran77语言编写程序。计算中网格点数为10121。取121.0,1,0.1,1.0,0Ihpp。在100Re的情况下,通过计算可以求出速度分布为:2500.01y(D.14)图...