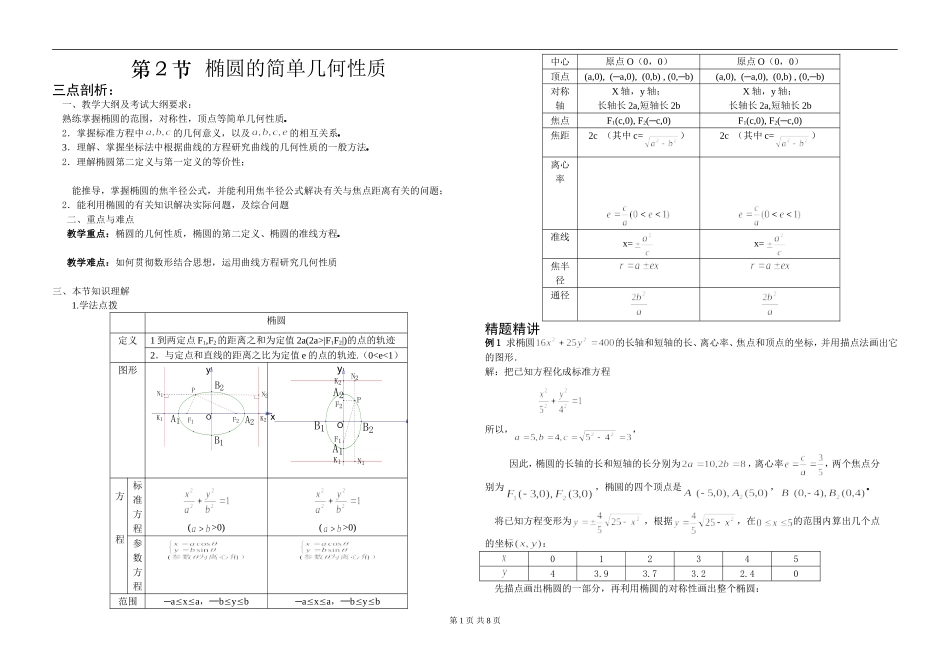
第2节椭圆的简单几何性质三点剖析:一、教学大纲及考试大纲要求:熟练掌握椭圆的范围,对称性,顶点等简单几何性质奎屯王新敞新疆2.掌握标准方程中的几何意义,以及的相互关系奎屯王新敞新疆3.理解、掌握坐标法中根据曲线的方程研究曲线的几何性质的一般方法奎屯王新敞新疆2.理解椭圆第二定义与第一定义的等价性;能推导,掌握椭圆的焦半径公式,并能利用焦半径公式解决有关与焦点距离有关的问题;2.能利用椭圆的有关知识解决实际问题,及综合问题二、重点与难点教学重点:椭圆的几何性质,椭圆的第二定义、椭圆的准线方程奎屯王新敞新疆教学难点:如何贯彻数形结合思想,运用曲线方程研究几何性质三、本节知识理解1.学法点拨椭圆定义1到两定点F1,F2的距离之和为定值2a(2a>|F1F2|)的点的轨迹2.与定点和直线的距离之比为定值e的点的轨迹.(00)(>0)参数方程范围─axa,─byb─axa,─byb中心原点O(0,0)原点O(0,0)顶点(a,0),(─a,0),(0,b),(0,─b)(a,0),(─a,0),(0,b),(0,─b)对称轴X轴,y轴;长轴长2a,短轴长2bX轴,y轴;长轴长2a,短轴长2b焦点F1(c,0),F2(─c,0)F1(c,0),F2(─c,0)焦距2c(其中c=)2c(其中c=)离心率准线x=x=焦半径通径精题精讲例1求椭圆的长轴和短轴的长、离心率、焦点和顶点的坐标,并用描点法画出它的图形.解:把已知方程化成标准方程所以,,因此,椭圆的长轴的长和短轴的长分别为,离心率,两个焦点分别为,椭圆的四个顶点是,奎屯王新敞新疆将已知方程变形为,根据,在的范围内算出几个点的坐标:01234543.93.73.22.40先描点画出椭圆的一部分,再利用椭圆的对称性画出整个椭圆:第1页共8页4-45-5xOy例2在同一坐标系中画出下列椭圆的简图,并求出顶点坐标和离心率。(1)(2)答:简图如下:4-45-5-33xOy例3分别在两个坐标系中,画出以下椭圆的简图并比较它们的离心率。(1)(2)答:简图如下:奎屯王新敞新疆2-23-3xOy6-67-7xOy例4写出下列椭圆的准线方程:(1)(2)奎屯王新敞新疆解:⑴方程可化为,是焦点在轴上且,的椭圆奎屯王新敞新疆所以此椭圆的准线方程为奎屯王新敞新疆⑵方程是焦点在轴上且,的椭圆奎屯王新敞新疆所以此椭圆的准线方程为奎屯王新敞新疆例5.分别求出符合下列条件的椭圆的标准方程.(1)椭圆过(3,0)点,离心率e=。(2)过点(3,-2)且与椭圆有相同焦点。(3)长轴长与短轴长之和为10,焦距为。(4)中心在原点,离心率为,准线方程为。(5)中心在原点,对称轴在坐标轴上,x轴上的一个焦点与短轴两端点的连线互相垂直,且此焦点与长轴上较近的端点距离是。【解】当椭圆的焦点在x轴上时, a=3,=,∴c=.从而b2=a2-c2=9-6=3,∴椭圆的方程为=1.当椭圆的焦点在y轴上时, b=3,=,∴=,∴a2=27.∴椭圆的方程为=1.∴所求椭圆的方程为=1或=1.例6求满足下列条件的椭圆的离心率.(1)若椭圆两准线间的距离是该椭圆焦距的2倍.(2)若椭圆的一个顶点与它的两个焦点构成的三角形是等边三角形.(3)设为椭圆的两个焦点,以为圆心过椭圆中心的圆与椭圆有一个交点M,若直线与圆相切.(4)若分别为椭圆的左、右焦点,P是以为直径的圆与椭圆的一个第2页共8页交点,且.例7已知椭圆与轴的正半轴交于A,O是原点,若椭圆上存在一点M,使MA⊥MO,求椭圆离心率的取值范围奎屯王新敞新疆例8椭圆上有一点P,它到椭圆的左准线距离为10,求点P到椭圆的右焦点的距离奎屯王新敞新疆解:椭圆的离心率为,根据椭圆的第二定义得,点P到椭圆的左焦点距离为奎屯王新敞新疆再根据椭圆的第一定义得,点P到椭圆的右焦点的距离为20-8=12奎屯王新敞新疆例9设分别为椭圆的左、右焦点,是椭圆上一点,求证:奎屯王新敞新疆例10椭圆,其上一点P(3,)到两焦点的距离分别是6.5和3.5,求椭圆方程奎屯王新敞新疆解:由椭圆的焦半径公式,得,解得,从而有奎屯王新敞新疆所求椭圆方程为奎屯王新敞新疆例11已知椭圆的中心在原点,长轴在x轴上,离心率,已知点到这个椭圆上的点的最远距离是,求这个椭圆方程.例12已知是椭圆的两个焦点,点P是椭圆上一点.(1)若,求的面积;(2)若为...