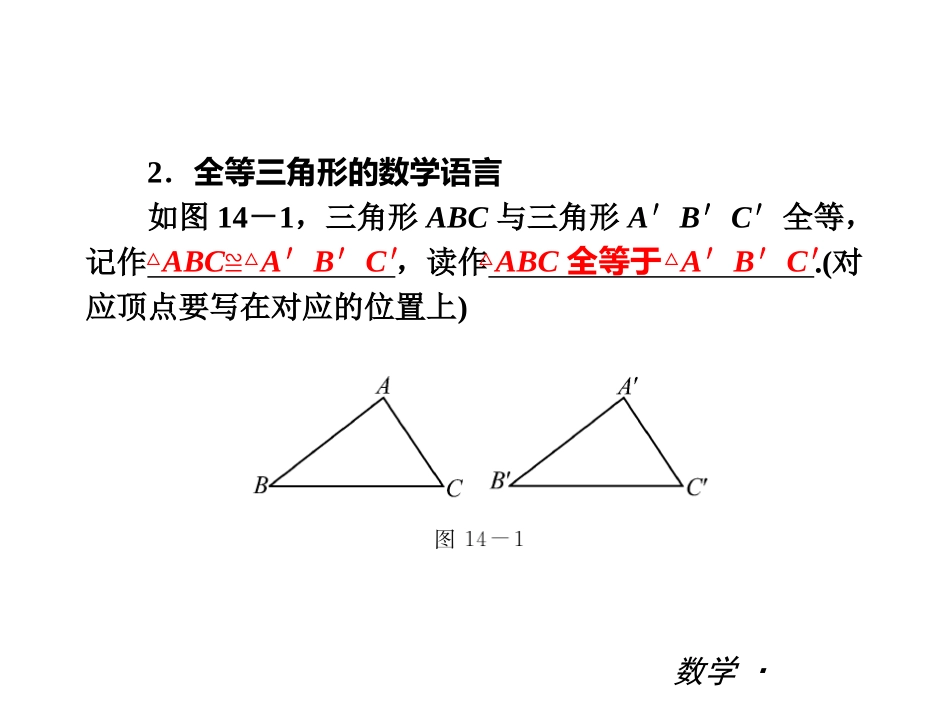
数学·沪科版(HK)第15章复习第14章|复习知识归纳数学·沪科版(HK)1.全等三角形及其相关概念(1)能够的两个图形叫做全等形;能够的两个三角形叫做全等三角形.(2)全等三角形中的边叫做对应边,全等三角形中的角叫做对应角,全等三角形中的顶点叫做对应顶点.完全重合完全重合互相重合互相重合互相重合第14章|复习数学·沪科版(HK)2.全等三角形的数学语言如图14-1,三角形ABC与三角形A′B′C′全等,记作,读作.(对应顶点要写在对应的位置上)△ABC≌△A′B′C′△ABC全等于△A′B′C′第14章|复习数学·沪科版(HK)3.全等三角形的性质(1)全等三角形的相等;全等三角形的相等.(2)全等三角形对应边上的高、对应边上的中线、对应角平分线分别.(3)全等三角形的周长,面积.对应边对应角相等相等相等第14章|复习数学·沪科版(HK)4.三角形全等的判定方法(1)对应相等的两个三角形全等.简记为“边角边”或“SAS”.(2)对应相等的两个三角形全等.简记为“角边角”或“ASA”.(3)对应相等的两个三角形全等.简记为“边边边”或“SSS”.只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定,这个性质叫做三角形的稳定性.两边和它们的夹角两角和它们的夹边三边第14章|复习数学·沪科版(HK)(4)对应相等的两个三角形全等.简记为“角角边”或“AAS”.(5)直角三角形全等的判定:对应相等的两个直角三角形全等.简记为“斜边、直角边”或“HL”.5.全等三角形的证明书写格式定理应用时的书写格式:第一步,先指出在哪两个三角形中证全等——在△ABC和△A′B′C′中;第二步,按定理中边与角的顺序列出三个条件;第三步,写出结论——△ABC≌△A′B′C′.两个角和其中一个角的对边斜边和一条直角边第14章|复习考点攻略数学·沪科版(HK)►考点一全等三角形的性质例1如图14-2所示,△ABC≌△AEF,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确的结论有()A.1个B.2个C.3个D.4个C第14章|复习数学·沪科版(HK)[解析]由全等三角形的性质,可得AC=AF,EF=BC,∠EAF=∠BAC,所以∠EAF-∠BAF=∠BAC-∠BAF,即∠EAB=∠FAC,因此只有②不正确.第14章|复习数学·沪科版(HK)方法技巧全等三角形的“对应边相等、对应角相等”的性质,是我们由全等三角形获得相等线段和相等角的重要依据.第14章|复习数学·沪科版(HK)►考点二全等三角形的判定例2如图14-3,已知AC∥DF,且BE=CF.(1)请你只添加一个条件,使△ABC≌△DEF,你添加的条件是______________________________________________________________;(2)添加条件后,证明△ABC≌△DEF.AC=DF(或AB∥DE或∠B=∠DEF或∠A=∠D)(有一个即可)第14章|复习数学·沪科版(HK)[解析]根据AC∥DF,可得∠ACB=∠F,又BE=CF,所以BC=EF,可添加条件是AC=DF或AB∥DE或∠B=∠DEF或∠A=∠D.第14章|复习数学·沪科版(HK)解:(1)AC=DF(或AB∥DE或∠B=∠DEF或∠A=∠D)(有一个即可)(2)添加条件为AC=DF时,证明: AC∥DF,∴∠ACB=∠F. BE=CF,∴BC=EF,在△ABC和△DEF中,BC=EF,∠ACB=∠F,AC=DF,∴△ABC≌△DEF.第14章|复习数学·沪科版(HK)方法技巧全等三角形的判定是中考的基本考点,也是必考知识点.要判定△ABC和△DEF全等,根据已知条件可得一边一角,并且边和角是相邻的,所以我们可以选择另两对对应角中的任何一对对应角或夹这个角的另一对对应边,这样就可以利用角角边或边角边来判定,若选择这个角的对边就是错误的,因此同学们要学会灵活应用全等三角形的判定.第14章|复习数学·沪科版(HK)►考点三全等三角形的画法例3已知一个三角形的两条边长分别是1cm和2cm,一个内角为40°.(1)请你借助图14-4画出一个满足题设条件的三角形;(2)你是否还能画出既满足题设条件,又与(1)中所画的三角形不全等的三角形?若能,请你在用“尺规作图”作出所有这样的三角形;若不能,请说明理由;(3)如果将题设条件改为“三角形的两条边长分别是3cm和4cm,一个内角为40°”,那么满足这一条件,且彼此不全等的三角形共有________个.4第14章|复习数学·沪科...