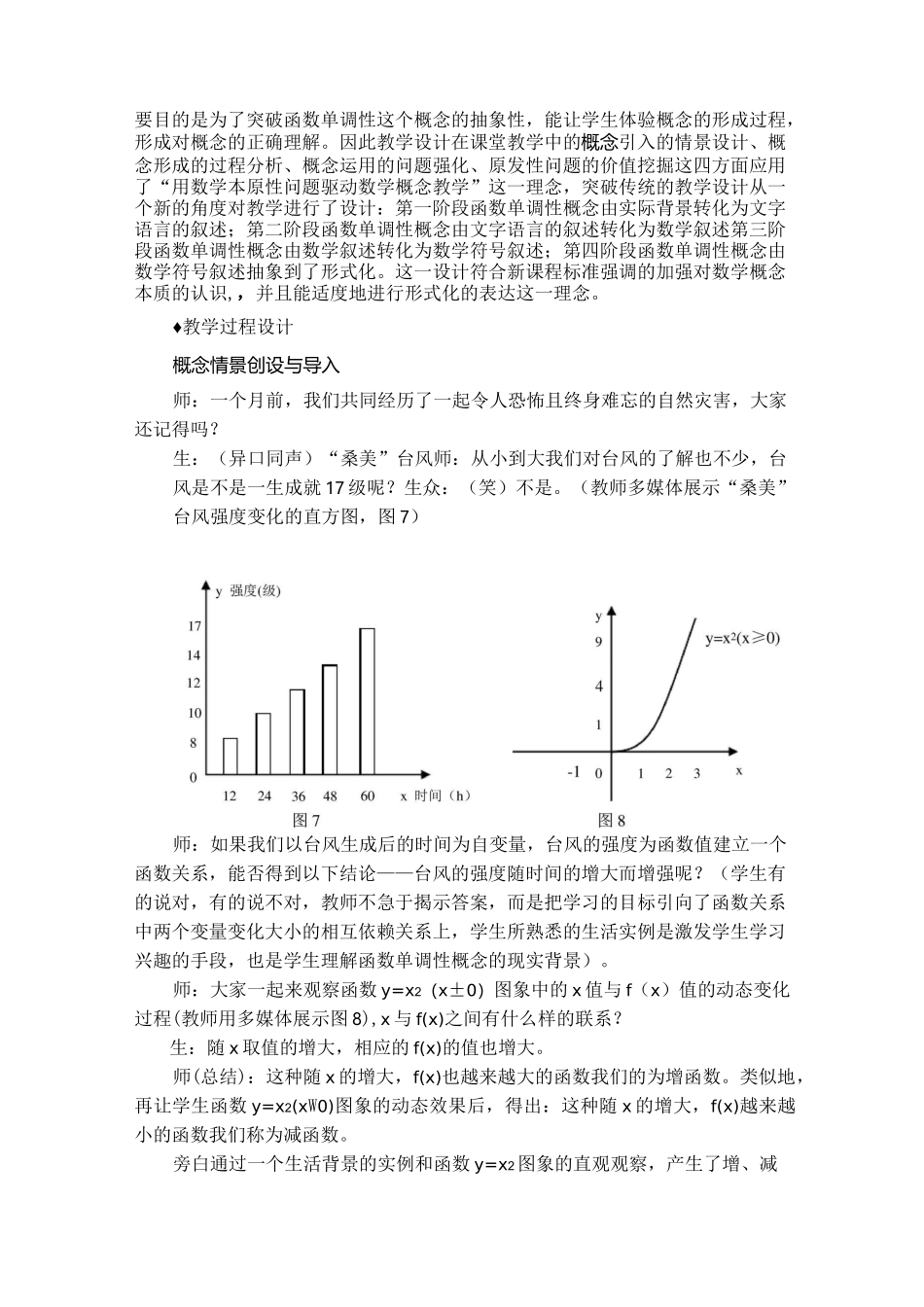
《函数单调性》教学设计基于函数单调性概念是高中教材中形式化程度较强,学生较难理解以及要让学生充分了解概念后面所蕴涵的数学思想的主张,笔者以“数学本原性问题驱动”数学概念教学为指导理念,在对函数单调性概念在高中教材中的地位和作用进行详细分析的基础上进行了新的教学设计及课堂实录。♦教材分析教材的地位和作用《函数的单调性》是《高中数学人教A版》(必修1)第一章1.31节的内容。它既是在学生学过函数概念等知识后的延续和拓展,又是后面研究指数函数、对数函数、三角函数等各类函数的单调性的基础,在整个高中数学中起着承上启下的作用。研究函数单调性的过程体现了数学的数形结合和归纳转化的思想方法,反映了从特殊到一般的数学归纳思维形式,这对培养学生的创新意识、发展学生的思维能力,掌握数学的思想方法具有重大意义。函数的单调性是函数的四个基本性质之一,在比较几个数的大小、对函数作定性分析(求函数的值域、最值,求函数解析式的参数范围、绘函数图象)以及与不等式等其它知识的综合应用上都有广泛的应用;同时在这一节中利用函数图象来研究函数性质的数形结合的思想将贯穿于我们整个高中数学教学。教材的重点与难点教学重点:(1)领会函数单调性概念,体验函数单调性的形式化过程,深刻理解函数单调性的本质,并明确单调性是一个局部概念;()函数单调性概念的应用教学难点:突破抽象,深刻理解函数单调性形式化的概念。♦教学目标分析根据新课标的要求和教学内容的结构特征,依据学生学习认知的心理规律和素质教育的要求,结合学生的实际水平,本节课教学目标如下:知识目标:()从本质上理解函数单调性概念;()运用形式化的函数单调性概念进行判断与应用。能力目标:()培养学生的观察能力,分析归纳能力,领会归纳转化的思想方法。()使学生体验和理解从特殊到一般的数学归纳推理思维方式。()培养学生从具体到抽象的能力。情感目标:()培养学生主动探索、不畏困难、敢于创新的意识和精神。()通过本课的学习,使学生能理性地思考生活中的增长、递减现象。♦设计理念本教学设计是基于用数学本原性问题来驱动数学概念的理念进行设计的。主要目的是为了突破函数单调性这个概念的抽象性,能让学生体验概念的形成过程,形成对概念的正确理解。因此教学设计在课堂教学中的概念引入的情景设计、概念形成的过程分析、概念运用的问题强化、原发性问题的价值挖掘这四方面应用了“用数学本原性问题驱动数学概念教学”这一理念,突破传统的教学设计从一个新的角度对教学进行了设计:第一阶段函数单调性概念由实际背景转化为文字语言的叙述;第二阶段函数单调性概念由文字语言的叙述转化为数学叙述第三阶段函数单调性概念由数学叙述转化为数学符号叙述;第四阶段函数单调性概念由数学符号叙述抽象到了形式化。这一设计符合新课程标准强调的加强对数学概念本质的认识,,并且能适度地进行形式化的表达这一理念。♦教学过程设计概念情景创设与导入师:一个月前,我们共同经历了一起令人恐怖且终身难忘的自然灾害,大家还记得吗?生:(异口同声)“桑美”台风师:从小到大我们对台风的了解也不少,台风是不是一生成就17级呢?生众:(笑)不是。(教师多媒体展示“桑美”台风强度变化的直方图,图7)师:如果我们以台风生成后的时间为自变量,台风的强度为函数值建立一个函数关系,能否得到以下结论——台风的强度随时间的增大而增强呢?(学生有的说对,有的说不对,教师不急于揭示答案,而是把学习的目标引向了函数关系中两个变量变化大小的相互依赖关系上,学生所熟悉的生活实例是激发学生学习兴趣的手段,也是学生理解函数单调性概念的现实背景)。师:大家一起来观察函数y=x2(x±0)图象中的x值与f(x)值的动态变化过程(教师用多媒体展示图8),x与f(x)之间有什么样的联系?生:随x取值的增大,相应的f(x)的值也增大。师(总结):这种随x的增大,f(x)也越来越大的函数我们的为增函数。类似地,再让学生函数y=x2(xW0)图象的动态效果后,得出:这种随x的增大,f(x)越来越小的函数我们称为减函数。旁白通过一个生活背景的实例和函数y=x2图象的直观...