正弦定理（）VIP免费

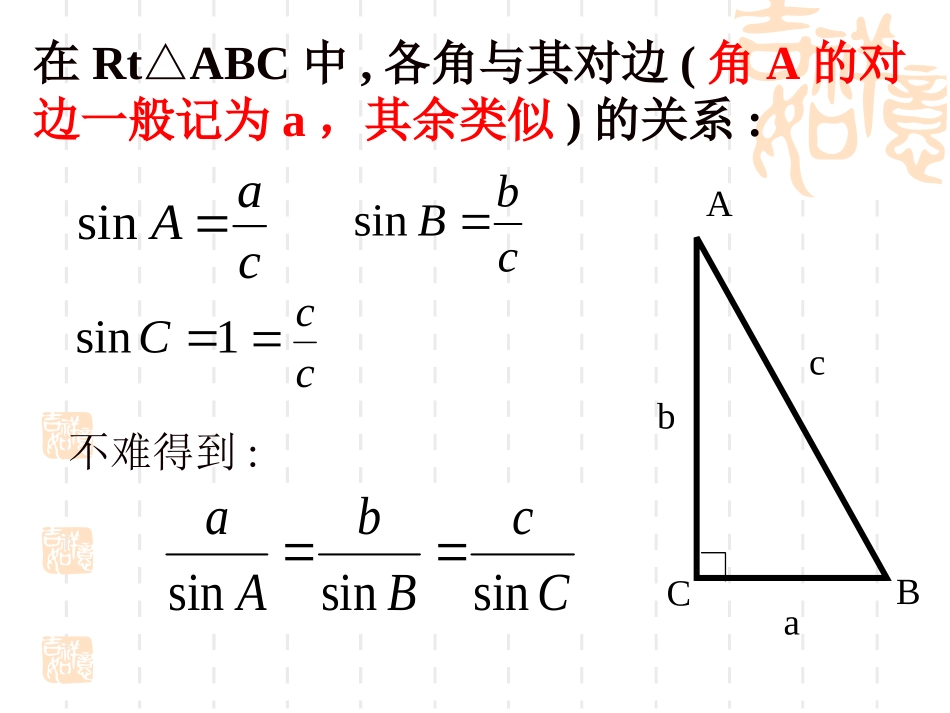
正弦定理正弦定理正弦定理正弦定理正弦定理一、创设情境一、创设情境例1、如图，船从港口B航行到港口C，测得BC的距离为600m，船在港口C卸货后继续向港口A航行，船上有测角仪测得A=75°，C=45°，能否计算出AB的距离？A.B..C在RtABC△中,各角与其对边(角A的对边一般记为a，其余类似)的关系:caAsincbBsin1sinC不难得到:CcBbAasinsinsinCBAabccc在钝角三角形ABC中有这样的关系吗?CAcbBaDCCbADsinsin）（且CcBbAasinsinsin可得：此时有cADBsin过点A作ADBC⊥，CcBbAasinsinsin即在一个三角形中,各边和它所对角的正弦的比相等.思考：你能否找到其他证明正弦定理的方法？二、正弦定理二、正弦定理（R为△ABC外接圆半径）另证1:RCcBbAa2sinsinsin证明：OC/cbaCBARCcRcCCCCCBA2sin2sinsin,90''RCcBbAaRBbRAa2sinsinsin2sin,2sin同理作外接圆O,过B作直径BC/,连AC/,三、定理变形三、定理变形3.2sin,2sin,2sinaRAbRBcRC变式sinsin1.sinsinbAcAaBC变式sinsin2.sinaBaCAbc变式4.::sin:sin:sinabcABC变式（边化角）（角化边）一般地，把三角形的三个角A，B，C和它们的对边a，b，c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫解三角形。四、正弦定理的应用四、正弦定理的应用1、利用正弦定理解三角形：①已知三角形的任意两角和一边，求其他角和边②已知三角形的任意两边和其中一边的对角，求另一边的对角，进而可求其他的边和角2、判断三角形的形状：（边角转化）（注意解的个数）五、三角形面积公式五、三角形面积公式111sinsinsin222ABCSabCbcAacB证明：∵aABCahS21CbBcADhasinsin∴CabBacSABCsin21sin21同理AbcSABCsin21BACDabcha已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?课后思考