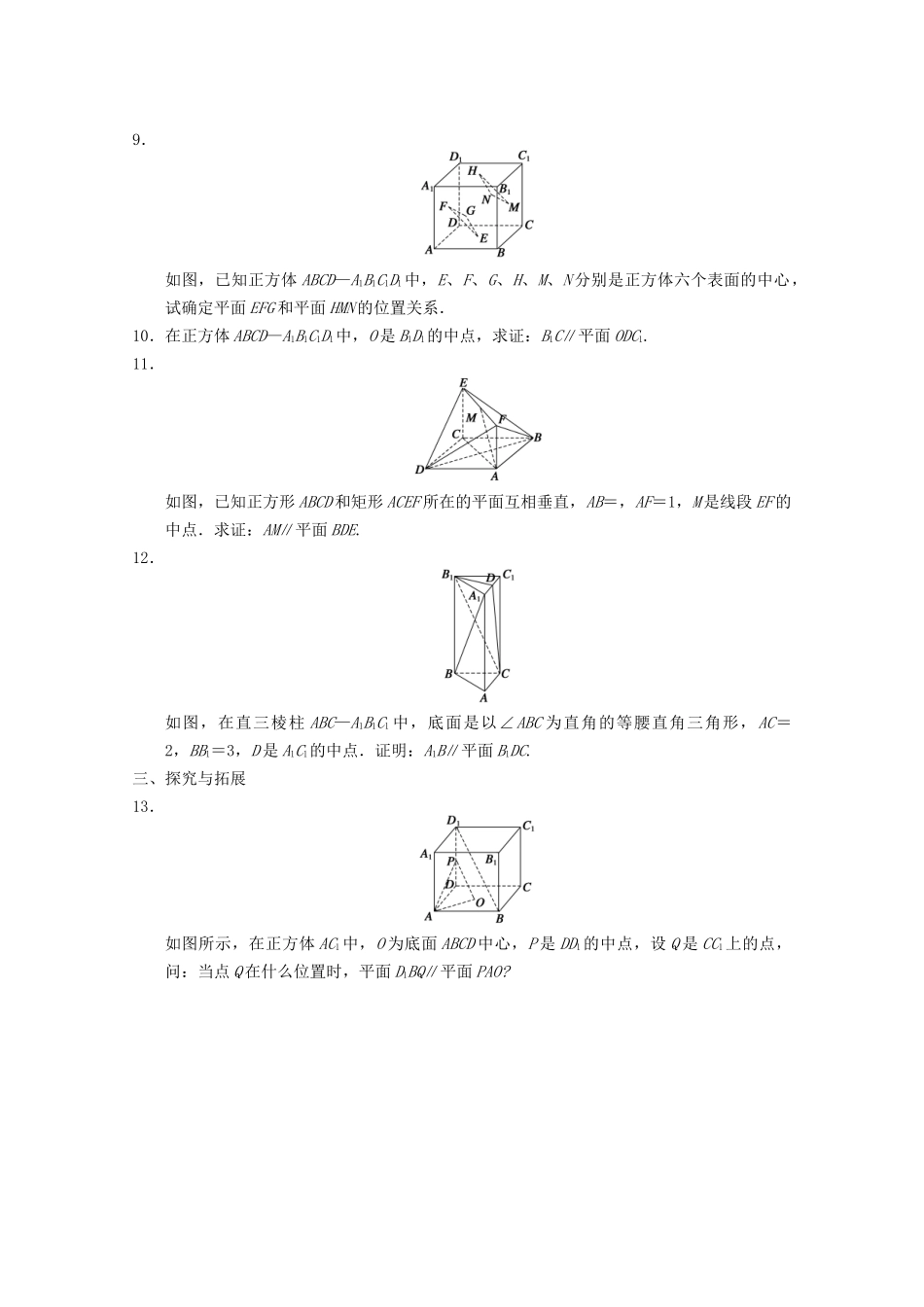
3.2.2空间线面关系的判定(一)——平行关系的判定一、基础过关1.空间直角坐标系中A(1,2,3),B(-1,0,5),C(3,0,4),D(4,1,3),则直线AB与CD的位置关系为________(平行、垂直或无法确定).2.已知平面α的一个法向量是n=(1,1,1),A(2,3,1),B(1,3,2),则直线AB与平面α的关系是______________.3.已知直线l与平面α垂直,直线的一个方向向量为u=(1,3,z),向量v=(3,-2,1)与平面α平行,则z=________.4.已知A(0,0,0),B(1,0,0),C(0,1,0),D(1,1,x),若AD⊂平面ABC,则实数x的值是_____.5.若平面α的一个法向量为u1=(-3,y,2),平面β的一个法向量为u2=(6,-2,z),且α∥β,则y+z=________.6.如图,在平行六面体ABCD—A1B1C1D1中,M、P、Q分别为棱AB、CD、BC的中点,若平行六面体的各棱长均相等,则①A1M∥D1P;②A1M∥B1Q;③A1M∥平面DCC1D1;④A1M∥平面D1PQB1.以上结论中正确的是__________(填序号).二、能力提升7.在正方体ABCD—A1B1C1D1中,棱长为a,M、N分别为A1B、AC上的点,A1M=AN=a,则MN与平面BB1C1C的位置关系是________.8.如图所示,正四棱柱ABCD—A1B1C1D1中,E、F、G、H分别是CC1、C1D1、D1D、DC的中点,N是BC中点,点M的四边形EFGH及其内部运动,则M只须满足条件________时,MN∥平面B1BDD1(请填上你认为正确的一条即可).9.如图,已知正方体ABCD—A1B1C1D1中,E、F、G、H、M、N分别是正方体六个表面的中心,试确定平面EFG和平面HMN的位置关系.10.在正方体ABCD—A1B1C1D1中,O是B1D1的中点,求证:B1C∥平面ODC1.11.如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=,AF=1,M是线段EF的中点.求证:AM∥平面BDE.12.如图,在直三棱柱ABC—A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2,BB1=3,D是A1C1的中点.证明:A1B∥平面B1DC.三、探究与拓展13.如图所示,在正方体AC1中,O为底面ABCD中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO?答案1.平行2.AB∥α或AB⊂α3.34.05.-36.①③④7.平行8.M在FH上9.解如图,建立空间直角坐标系D—xyz,设正方体的棱长为2,易得E(1,1,0),F(1,0,1),G(2,1,1),H(1,1,2),M(1,2,1),N(0,1,1).∴EF=(0,-1,1),EG=(1,0,1),HM=(0,1,-1),HN=(-1,0,-1).设m=(x1,y1,z1),n=(x2,y2,z2)分别是平面EFG,平面HMN的法向量,由⇒令x1=1,得m=(1,-1,-1).由得令x2=1,得n=(1,-1,-1).∴m=n,故m∥n,即平面EFG∥平面HMN.10.证明建系如图,设正方体的棱长为1,则可得B1(1,1,1),C(0,1,0),O(,,1),C1(0,1,1),B1C=(-1,0,-1),OD=,OC1=.设平面ODC1的法向量为n=(x0,y0,z0),则得令x0=1,得y0=1,z0=-1,∴n=(1,1,-1).又B1C·n=-1×1+0×1+(-1)×(-1)=0,∴B1C⊥n,又B1C⊄平面ODC1,∴B1C∥平面ODC1.11.证明建立如图所示的空间直角坐标系.设AC∩BD=N,连结NE,则点N、E的坐标分别是、(0,0,1).∴NE=.又点A、M的坐标分别是(,,0)、,∴AM=.∴NE=AM,且A∉NE,∴NE∥AM.又∵NE⊂平面BDE,AM⊄平面BDE,∴AM∥平面BDE.12.证明如图,以B为坐标原点,分别以BA,BC,BB1所在直线为x轴,y轴,z轴建立空间直角坐标系,则B1(0,0,3),C(0,,0),D,A1(,0,3).A1B=(-,0,-3),DB1=,DC=,设平面B1DC的法向量为n=(x,y,z),则取n=,由于A1B·n=0,且A1B⊄平面B1DC,所以A1B∥平面B1DC.13.解如图所示,分别以DA、DC、DD1所在直线为x,y,z轴,建立空间直角坐标系,在CC1上任取一点Q,连结BQ,D1Q.设正方体的棱长为1,则O,P,A(1,0,0),B(1,1,0),D1(0,0,1),则Q(0,1,z),则OP=,BD1=(-1,-1,1),∴OP∥BD1,∴OP∥BD1.AP=,BQ=(-1,0,z),当z=时,AP=BQ,即AP∥BQ,有平面PAO∥平面D1BQ,∴当Q为CC1的中点时,平面D1BQ∥平面PAO.