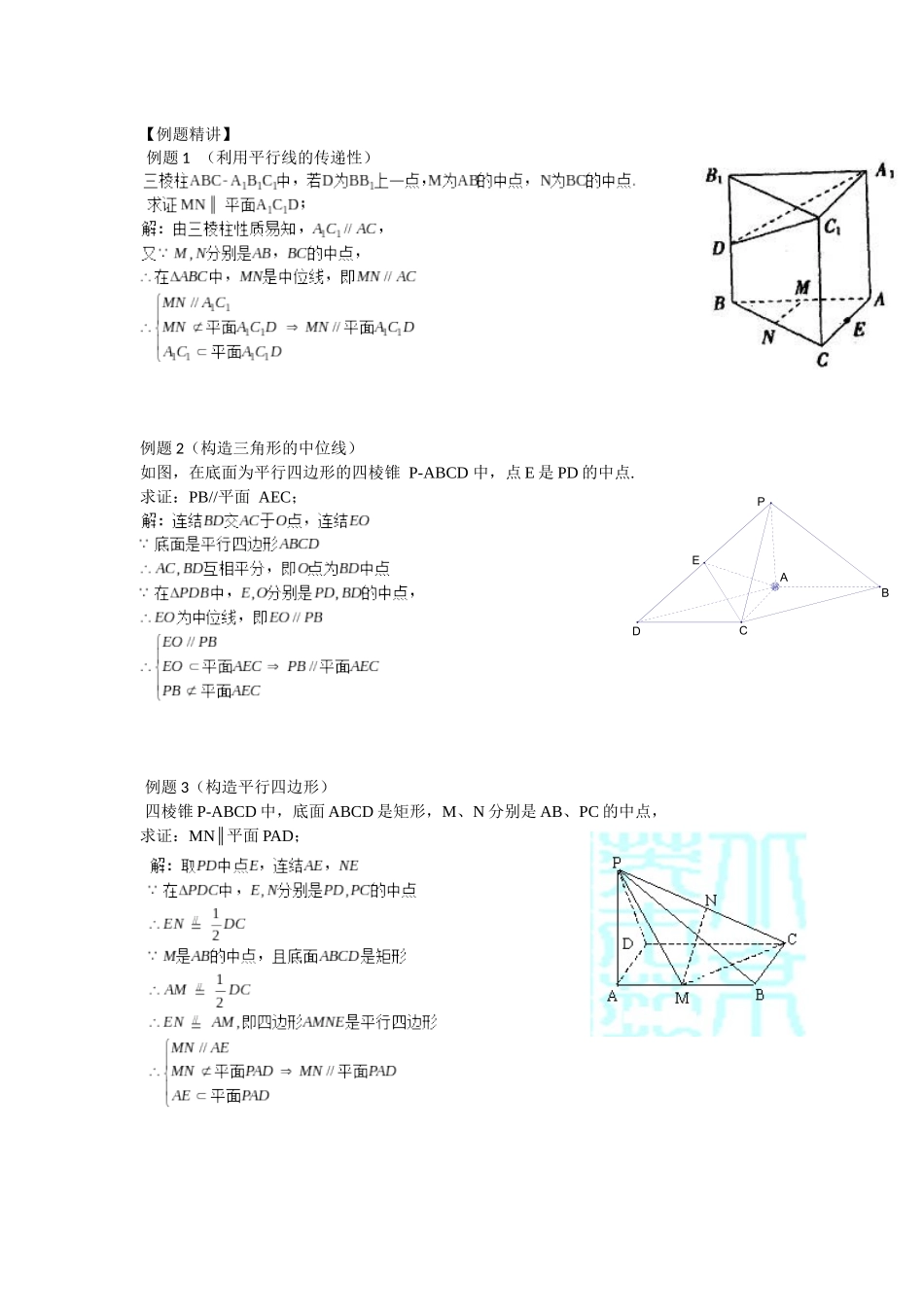
线面平行的证明要求:通过此次课程,熟练掌握对于“线面平行”该类题型的证明重点:该类题型主要出现在立体几何大题的第一小问,属于简单题,必拿题,主要着重于证明过程难点:对于题型分类不够清楚,不能快速地找到“突破口”【知识清单】1高中部分:a.直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。简记为:线线平行,则线面平行。符号表示:2初中部分:a.平行线的传递性b.三角形的中位线BCMNBCMNABCMNACABNMABC21//,的中位线,是的中点,则、分别是、中,在c.平行四边形的判定一组对边平行且相等的四边形是平行四边形3线面平行的题型分类:a.利用平行线的传递性b.构造三角形中位线c.构造平行四边形【例题精讲】例题1(利用平行线的传递性)例题2(构造三角形的中位线)如图,在底面为平行四边形的四棱锥P-ABCD中,点E是PD的中点.求证:PB//平面AEC;例题3(构造平行四边形)四棱锥P-ABCD中,底面ABCD是矩形,M、N分别是AB、PC的中点,求证:MN∥平面PAD;ABCDEP【课堂自测】1、在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别是AB,PC的中点.求证:MN∥平面PAD;2、如图,在三棱柱ABC—A1B1C1中,D是AC的中点。求证:AB1//平面DBC13、如图,在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点.求证:C1O//平面AD1B1.NMDCBAPB1BC1ACA1D【方法总结】平行线的传递性构造三角形中位线构造平行四边形A1BB1AC1CDASDCBE【课后练习】1.已知ABC-A1B1C1是底面是正三角形的棱柱,D是AC的中点,求证:AB1//平面DBC12.正四棱锥中,是侧棱的中点.求证:直线平面3.已知四棱锥P-ABCD中,底面ABCD是矩形,E、F分别是AB、PD的中点.求证:AF//平面PECABCDEFP4.图中几何体ABCD-A1B1C1D1是正四棱柱,E是棱BC的中点。求证:BD1//平面C1DE5.在三棱柱中,为中点.求证:平面;.6.在三棱柱ABC-A1B1C1中,M,N分别是CC1,AB的中点.求证:CN//平面AB1M.B1A1C1DCBANMC1B1A1CBA