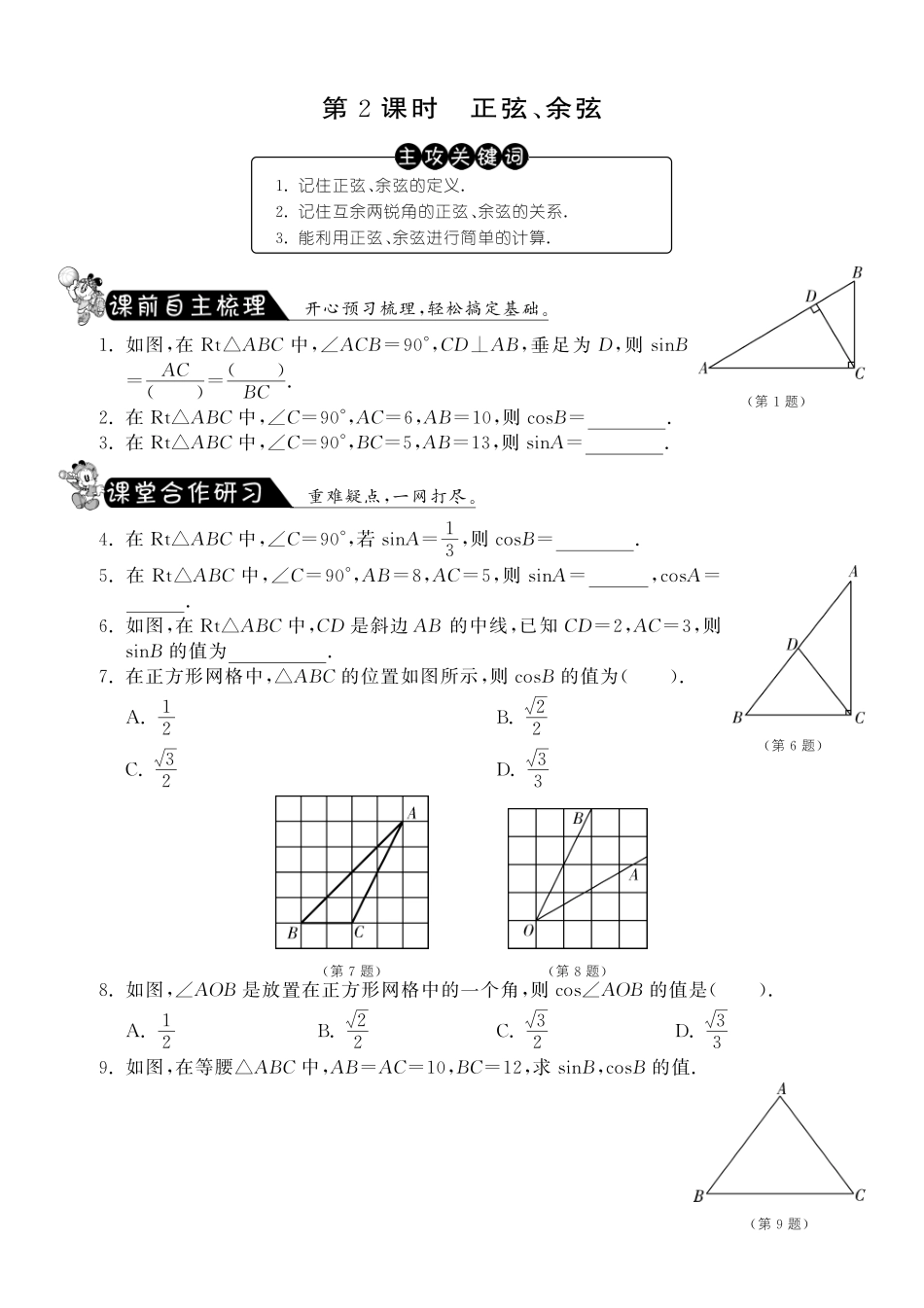
第2课时正弦、余弦1.记住正弦、余弦的定义.2.记住互余两锐角的正弦、余弦的关系.3.能利用正弦、余弦进行简单的计算.(第1题)开心预习梳理,轻松搞定基础.1.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则sinB=AC()=()BC.2.在Rt△ABC中,∠C=90°,AC=6,AB=10,则cosB=.3.在Rt△ABC中,∠C=90°,BC=5,AB=13,则sinA=.重难疑点,一网打尽.4.在Rt△ABC中,∠C=90°,若sinA=13,则cosB=.(第6题)5.在Rt△ABC中,∠C=90°,AB=8,AC=5,则sinA=,cosA=.6.如图,在Rt△ABC中,CD是斜边AB的中线,已知CD=2,AC=3,则sinB的值为.7.在正方形网格中,△ABC的位置如图所示,则cosB的值为().A.12B.22C.32D.33(第7题)(第8题)8.如图,∠AOB是放置在正方形网格中的一个角,则cos∠AOB的值是().A.12B.22C.32D.339.如图,在等腰△ABC中,AB=AC=10,BC=12,求sinB,cosB的值.(第9题)10.在Rt△ABC中,∠C=90°,cosA=1010,求sinA的值.源于教材,宽于教材,举一反三显身手.11.在Rt△ABC中,∠C=90°,cosA=35,AB=15,则AC的长是().A.3B.6C.9D.12(第12题)12.如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠DCA=45,BC=10,则AB的值是().A.3B.6C.8D.913.在Rt△ABC中,∠C=90°,sinA=825,则cosB=.14.已知在△ABC中,∠C=90°,3cosB=2,AC=25,则AB=.15.已知a,b,c分别是△ABC中∠A、∠B、∠C的对边,关于x的一元二次方程a(1-x2)+2bx+c(1+x2)=0有两个相等的实数根,且3c=a+3b.(1)判断△ABC的形状;(2)求sinA+sinB的值.(第16题)16.如图,在△ABC中,∠C=90°,AC=BC,BD为边AC上的中线,求sin∠ABD和tan∠ABD的值.瞧,中考曾经这么考!17.(2012浙江宁波)如图,在Rt△ABC中,∠C=90°,AB=6,cosB=23,则BC的长为().(第17题)A.4B.25C.18313D.12313第2课时正弦、余弦1.ABCD2.453.5134.135.398586.347.B8.B9.sinB=45,cosB=35.10.3101011.C12.B13.82514.615.(1)整理原方程,得(c-a)x2+2bx+(c+a)=0.依题意,得Δ=(2b)2-4(c-a)(c+a)=0,整理可得a2+b2=c2.故△ABC为直角三角形.(2)由3c=a+3b得a=3c-3b,代入a2+b2=c2,得(b-c)(5b-4c)=0.∵c>b,∴5b-4c=0,即b=45c.∴a=3c-3×45c()=35c.∴sinA=ac=35,sinB=bc=45,∴sinA+sinB=75.16.作DE⊥AB于点E.设DE=x,在等腰Rt△ADE中,∠A=45°,则AE=DE=x,AD=DEsin45°=2x.∵BD是边AC上的中线,∴CD=AD=2x,BC=AC=22x.∴BD=CD2+BC2=10x,BE=BD2-DE2=3x.∴sin∠ABD=DEBD=x10x=1010,tan∠ABD=DEBE=x3x=13.17.A