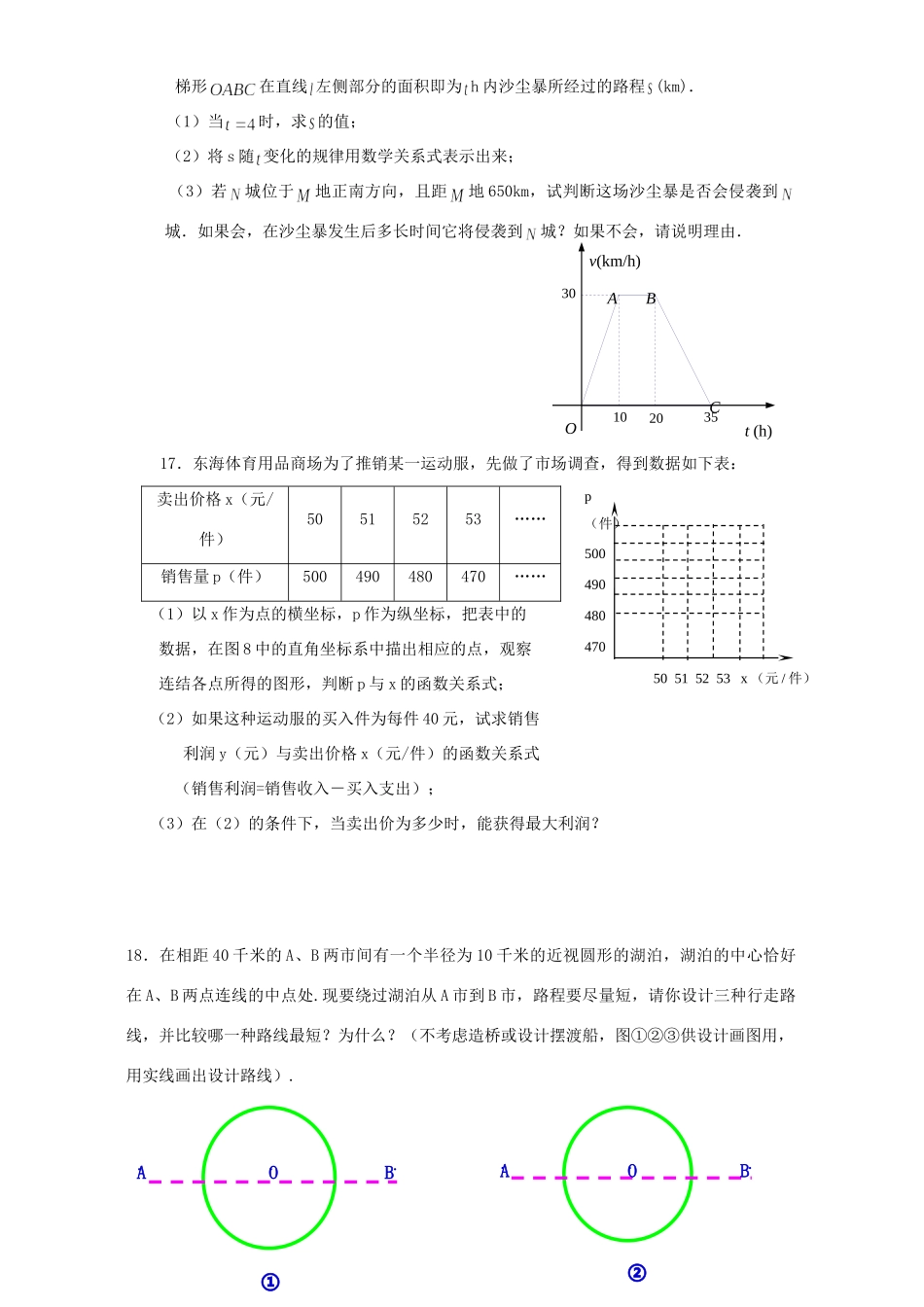
九年级数学综合训练题(四)一、选择题(本题共6个小题)1.方程x2-5x-1=0…………………………………………………………()A.有两个相等实B.有两个不等实根C.没有实根D.无法确定2.CD是RtΔABC的斜边AB上的高,AC=4,BC=3,则cos∠BCD的值是…………()A.B.C.D.3.已知⊙O和三点P、Q、R,⊙O的半径为3,OP=2,OQ=3,OR=4,经过这三点中的一点任意作直线总是与⊙O相交,这个点是………………………………………()A.PB.QC.RD.P或Q4.若一抛物线y=ax2与四条直线x=1,x=2,y=1,y=2围成的正方形有公共点,则a的取值范围是()A.≤a≤1B.≤a≤2C.≤a≤1D.≤a≤25.如图,已知⊙O的两条弦AB、CD相交于AB的中点E,且AB=4,DE=CE+3,则CD的长为…………………………………………………………………………………()A.4B.5C.8D.106.如图,Rt△ABC中,∠C=900,AC=4,BC=8,P是AB上一动点,直线PQ⊥AC于点Q,设AQ=x,则图中阴影部分的面积y与x之间的函数关系式的图象是…()二、填空题(本题共8个小题)7.求值:sin230°+cos230°=.8.已知⊙O1和⊙O2外切,半径分别为1cm和3cm,那么半径为5cm且分别与⊙O1、⊙O2都相切的圆一共可以作出个.9.半径分别为3cm和4cm的两圆,一条内公切线为7cm,则这条内公切线与连心线所夹锐角的度数为________.10.由梅州到广州的某一次列车,运行途中停靠的车站依次是:梅州——兴宁——华城——河源——惠州——东莞——广州,那么要为这次列车制作的火车票有种.5题11.设有反比例函数,、为其图象上的两点,若时,,则的取值范围是___________;12.已知二次函数的图象与x轴有交点,则a的取值范围是.13.已知一列数:1,―2,3,―4,5,―6,7,…将这列数排成下列形式:第1行1第2行-23第3行-45-6第4行7-89-10第5行11-1213-1415……按照上述规律排下去,那么第10行从左边数第5个数等于.14.如图,已知AD=30,点B、C是AD上的三等分点,分别以AB、BC、CD为直径作圆,圆心分别为E、F、G,AP切⊙G于点P,交⊙F于M、N两点,则弦MN的长是.三、解答下列各题:(本题共5个题)15.如图,是等边三角形,⊙O过点B,C,且与的延长线分别交于点D、E.弦∥,的延长线交的延长线于点G.(1)求证:是等边三角形;(2)若,,求的长.16.据某气象中心观察和预测:发生于地的沙尘暴一直向正南方向移动,其移动速度y(km/h)与时间(h)的函数图象如图所示.过线段上一点作横轴的垂线OGEBDCAFABCDEFGPMN···梯形在直线左侧部分的面积即为h内沙尘暴所经过的路程(km).(1)当时,求的值;(2)将s随变化的规律用数学关系式表示出来;(3)若城位于地正南方向,且距地650km,试判断这场沙尘暴是否会侵袭到城.如果会,在沙尘暴发生后多长时间它将侵袭到城?如果不会,请说明理由.17.东海体育用品商场为了推销某一运动服,先做了市场调查,得到数据如下表:卖出价格x(元/件)50515253……销售量p(件)500490480470……(1)以x作为点的横坐标,p作为纵坐标,把表中的数据,在图8中的直角坐标系中描出相应的点,观察连结各点所得的图形,判断p与x的函数关系式;(2)如果这种运动服的买入件为每件40元,试求销售利润y(元)与卖出价格x(元/件)的函数关系式(销售利润=销售收入-买入支出);(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?18.在相距40千米的A、B两市间有一个半径为10千米的近视圆形的湖泊,湖泊的中心恰好在A、B两点连线的中点处.现要绕过湖泊从A市到B市,路程要尽量短,请你设计三种行走路线,并比较哪一种路线最短?为什么?(不考虑造桥或设计摆渡船,图①②③供设计画图用,用实线画出设计路线).p(件)50049048047050515253x(元/件)35302010t(h)Ov(km/h)CAB②..ABO...ABO.①19.如图,在平面直角坐标系中,矩形ABCO的面积为15,且OA=OC+2,E为BC的中点,以OE为直径的⊙O′交y轴于D点,过D作DF⊥AE于点F.(1)求OA、OC的长;(2)求证:DF为⊙O′的切线;(3)小亮在解答本题时,发现△AOE是等腰三角形,且△AOE的面积是四边形ABCO面积的一半.由此,他根据自己过去解题的实践断定:“直线BC上一定存在除点E以...