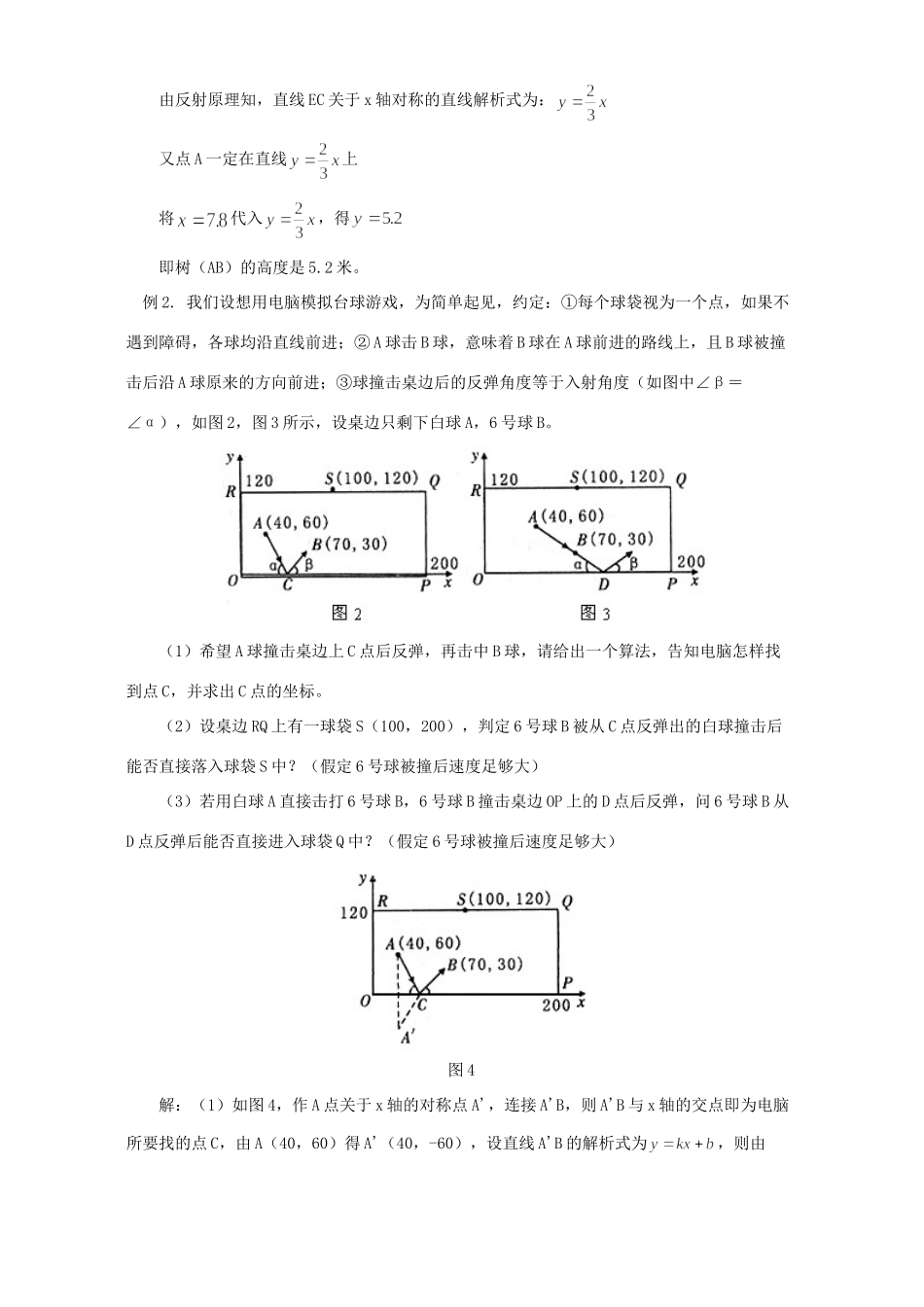
初中数学利用轴对称求一次函数解析式在平面直角坐标系中的任一点关于x轴的对称点是,关于y轴的对称点是,关于原点O的对称点是,那么这种对称性对函数的解析式又有什么影响呢?引例若直线与直线关于x轴对称,求k和b的值。分析:若直线与直线关于x轴对称,则直线上的点也必与直线上的点关于x轴一一对称,根据点关于x轴对称点为,知即用上述方法可以得出下列结论:①与直线关于x轴对称的直线解析式为;②与直线关于y轴对称的直线解析式为;③与直线关于原点O对称的直线解析式为。我们应用上述结论解决下列问题:例1.为了测量校园内一棵高不可攀的树的高度,学校数学应用实践小组作了如下探索——根据光的反射定律,利用一面镜子和一根皮尺设计如图1所示的测量方案:把镜子放在离树(AB)7.8米的点E处,然后沿着直线BE后退到点D处,这时恰好在镜子里看到树梢顶点A,再用皮尺量得米,观察者目高米,请你计算树(AB)的高度。图1分析:这道题我们通常用相似形来解决,在这里我们用函数方法来解其实也很简单。解:以E为坐标系原点,DB所在直线为x轴建立平面直角坐标系。则E点坐标为(0,0),C()所以直线EC的解析式为:由反射原理知,直线EC关于x轴对称的直线解析式为:又点A一定在直线上将代入,得即树(AB)的高度是5.2米。例2.我们设想用电脑模拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度(如图中∠β=∠α),如图2,图3所示,设桌边只剩下白球A,6号球B。(1)希望A球撞击桌边上C点后反弹,再击中B球,请给出一个算法,告知电脑怎样找到点C,并求出C点的坐标。(2)设桌边RQ上有一球袋S(100,200),判定6号球B被从C点反弹出的白球撞击后能否直接落入球袋S中?(假定6号球被撞后速度足够大)(3)若用白球A直接击打6号球B,6号球B撞击桌边OP上的D点后反弹,问6号球B从D点反弹后能否直接进入球袋Q中?(假定6号球被撞后速度足够大)图4解:(1)如图4,作A点关于x轴的对称点A',连接A'B,则A'B与x轴的交点即为电脑所要找的点C,由A(40,60)得A'(40,-60),设直线A'B的解析式为,则由,解得将代入,得出∴C点的坐标为(60,0)(2)因S(100,120)的坐标满足直线解析式∴6号球被从C点反弹出的白球撞击后,能够直接落入球袋S中。(3)如图5,若设白球A直接击打6号球B所走直线AB的解析式为,由A(40,60)、B(70,30),得,解得∵6号球B从D点反弹后所走直线的解析式与直线关于x轴对称∴其解析式为。当时,∴点Q(200,120)不在直线上因此6号球从D点反弹后不能直接进入球袋Q中。图5