九年级数学十月测试卷 北师大版试卷VIP免费

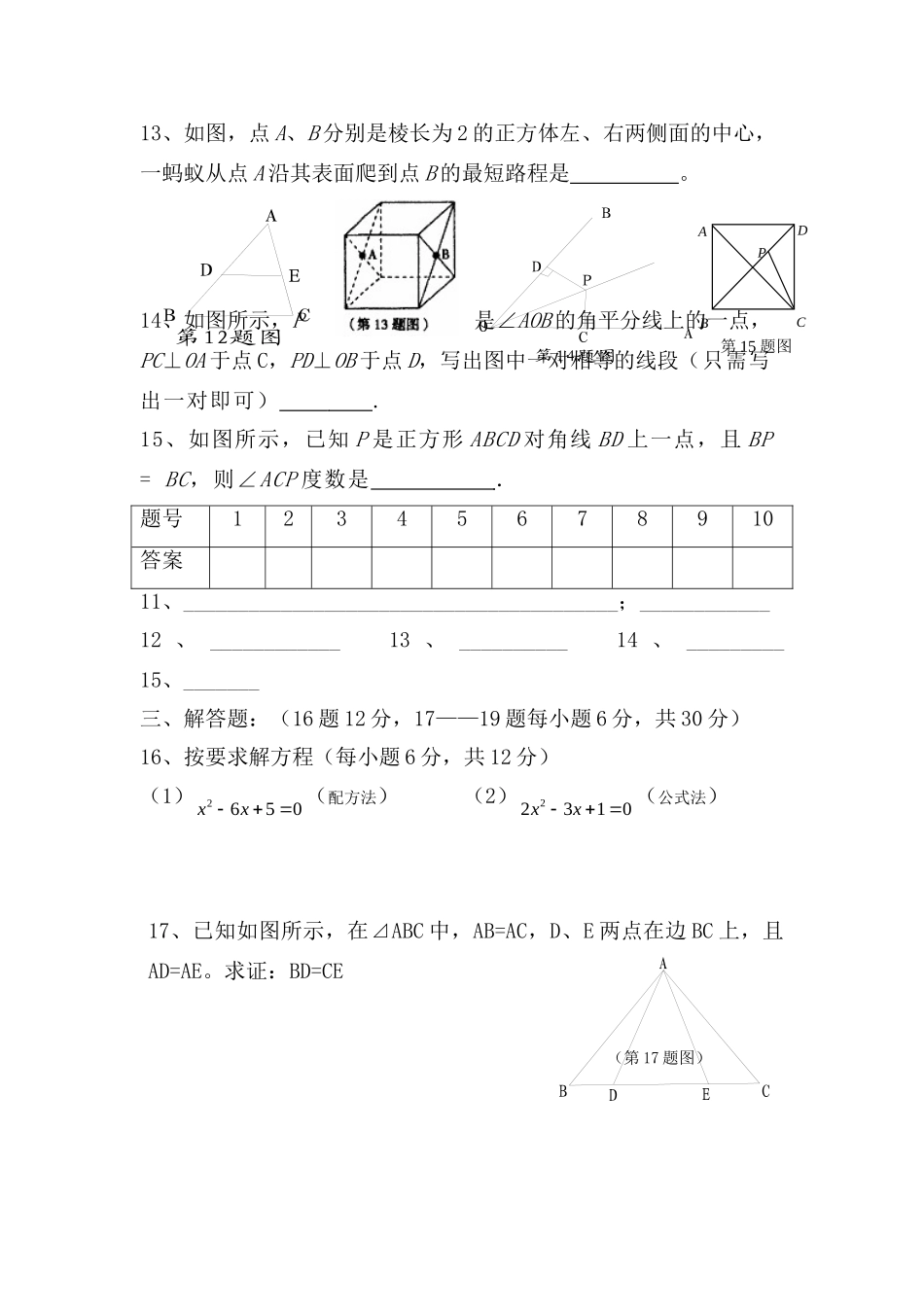
实验中学初三级十月测数学试卷（2009.10.8）题号一、二三四全卷得分1-151617-1819202122-2324得分(注意：请将选择题答案，填空题答案填在相应的位置)一、选择题：（每小题3分，共30分）1、顺次连接矩形各边中点所得的四边形一定是：（）A.等腰梯形B.正方形C.平行四边形D.菱形2、关于x的一元二次方程2(21)51xaxaax的一次项系数为4，则常数项为：（）A．1B．-1C．0D．53、甲公司前年缴税a万元，去年和今年缴税的年平均增长率均为b，则今年该公司应缴税（）万元。A．2%)1(baB．2)1(baC．2%)(abaD．2%)1(ba4、下列命题正确的是：（）A．对角线相等且互相平分的四边形是菱形.B．对角线相等且互相垂直的四边形是正方形.C．对角线相等且互相平分的四边形是矩形.D．对角线相等的四边形是等腰梯形.5、下列方程中，是一元二次方程的是：（）A.052yxB.232xxC.22)1(1xxxD.112xx6、如图所示，在△ABC与△DEF中，已有条件AB=DE，还需添加两考号：班别：姓名：座位号：座位号：个条件才能使△ABC≌△DEF，不能添加的一组条件是()A.∠B=∠E，BC=EFB.BC=EF，AC=DFC.∠A=∠D，∠B=∠ED.∠A=∠D，BC=EF7、如图所示，在平行四边形ABCD中，E是AB延长线上的一点，若60A，则1的度数为：（）A．120oB．60oC．45oD．30o8、如图所示，四边形ABCD为矩形，点O为对角线的交点，120BOC，BOAE交BO于点E，AB=4，则BE等于：()A.4B.3C.2D.19、已知AC，BD为菱形ABCD的对角线，且AC=12，BD=16.则菱形的周长为：()A.96B.64C.80D.4010、等腰ABC△两边的长分别是一元二次方程29180xx的两个解，则这个等腰三角形的周长是：（）A.12B.15C.12或15D.12和15二、填空：（每小题3分，共15分）11、命题“等腰三角形两底角相等”的逆命题是_______________________________________，逆命题是_________命题(填“真”或“假”).12、如图所示，在ABC△中，DE，分别是ABAC，的中点，若2cmBC，则DEcm．第7题图ABECD1第6题图FEDCBA第8题图EOCDBA13、如图，点A、B分别是棱长为2的正方体左、右两侧面的中心，一蚂蚁从点A沿其表面爬到点B的最短路程是。14、如图所示，P是∠AOB的角平分线上的一点，PC⊥OA于点C，PD⊥OB于点D，写出图中一对相等的线段（只需写出一对即可）.15、如图所示，已知P是正方形ABCD对角线BD上一点，且BP=BC，则∠ACP度数是．题号12345678910答案11、________________________________________；____________12、____________13、__________14、_________15、_______三、解答题：（16题12分，17——19题每小题6分，共30分）16、按要求解方程（每小题6分，共12分）（1）2650xx（配方法）（2）22310xx（公式法）17、已知如图所示，在⊿ABC中，AB=AC，D、E两点在边BC上，且AD=AE。求证：BD=CE（第17题图）第15题图BCDAPEDCBA第12题图EDCBA第14题图CDPBOA18、已知关于x的方程：2(2)(1)60mmmxmx是一元二次方程，试求m的值19、如图，已知在正方形ABCD中，E是AB的中点，延长BC到点F使CF＝AE．（1）求证：DE=DF（2）若H点为BC的中点，求证：AHED四、解答题：（本题共5个小题，每题9分，共45分）20、如图所示，在一块长92m，宽60m的矩形耕地上挖三条水渠（水渠的宽都相等），水渠把耕地分成面积均为8852m的6个矩形小块，水渠应挖多宽？考号：班别：姓名：(第19题图)GFHEDABC第20题图21、已知：如图，在△ABC中，AB＝AC，ADBC，垂足为D，AN是△ABC外角CAM的平分线，CEAN，垂足为E，连接DE交AC于F（1）求证：四边形ADCE为矩形（2）求证：DF∥AB，DF＝12AB22、已知关于x的一元二次方程：222(1)10xaxa有两个不相等的实数根12xx，；且有12112xx，求a的值及方程两根12xx，。座位号：座位号：第21题图FNEDCBMA23、某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利44元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价2元，商场平均每天可多售出5件。若商场平均每天要盈利1600元，每件衬衫应降价多少元？24、如图11所示，在四边形ABCD中，点E是线段AD上的任意一点（E与AD，不重合），GFH，，分别是BEBCCE，，的中点．（1）证明：四边形EGFH是平行四边形；（2）在（1）的条件下，若EFBC，且12EFBC，证明平行四边形EGFH是正方形．图11HGCFBDEA