九年级数学下学期适应性调研(二模)试卷答案 051629VIP免费

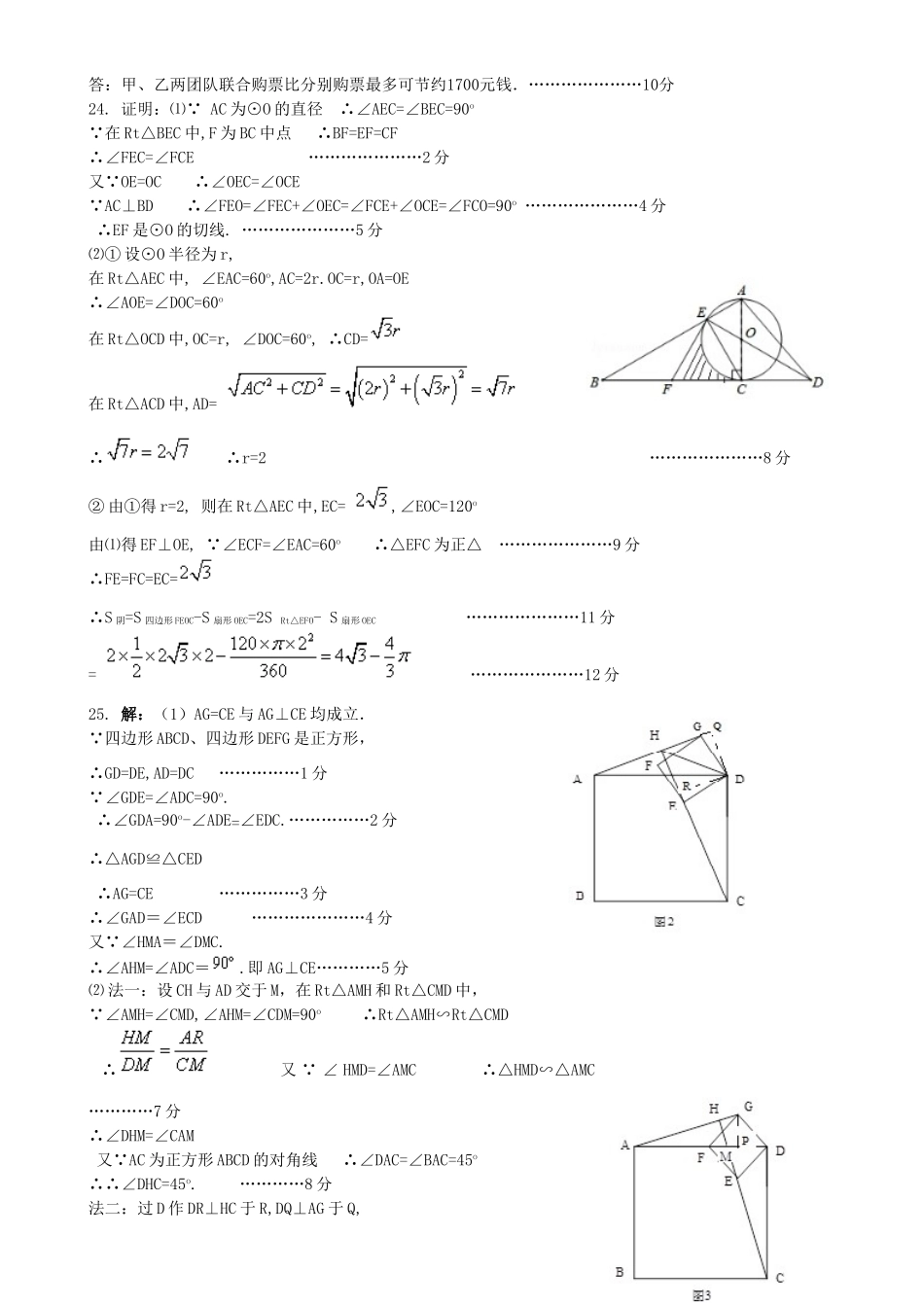
九年级数学参考答案一、选择题ADBBCC二、填空题7.(a-3)(a+3)8.m<99.1310.1211.4512.13.﹣7＜x＜﹣114.1615.x3=﹣5，x4=﹣216.三、解答题17.解：原式=……………4分=．…………………5分(2)解：原式=……………2分=……4分=…………………5分18.解：（1）方程两边都乘以（x﹣2）得，1=x﹣1﹣3（x﹣2），解得x=2，………………………………3分检验：当x=2时，x﹣2=2﹣2=0，……………………4分所以，原分式方程无解.………………………………5分（2）解不等式①得，x≥﹣1，………………………………2分解不等式②得，x＜2，………………………………4分所以，不等式组的解集是﹣1≤x＜2．………………………………5分19.解:（1）三次传球所有可能的情况如图：………………………………4分（2）由图知：三次传球后，球回到甲的概率为P（甲）=，即；……………6分由图知：三次传球后，球回到乙的概率为P（乙）=，……………………7分P（乙）>P（甲），所以是传到乙脚下的概率要大.………………………………8分20.解：（1）调查的总人数是：224÷40%=560（人）；………2分（2）“主动质疑”所在的扇形的圆心角的度数是：360×=54°；………4分（3）“讲解题目”的人数是：560﹣84﹣168﹣224=84（人）．图略………6分（4）在试卷评讲课中，“独立思考”的初三学生约有：6000×=1800（人）．……8分21.解：（1）作CH⊥AB于H．------------------------------------1分在Rt△ACH中，CH=AC•sin∠CAB=AC•sin25°≈10×0.42=4.2千米，AH=AC•cos∠CAB=AC•cos25°≈10×0.91=9.1千米，----------------3分在Rt△BCH中，BH=CH÷tan∠CBA=4.2÷tan37°≈4.2÷0.75=5.6千米，-----4分∴AB=AH+BH=9.1+5.6=14.7千米．故改直的公路AB的长14.7千米；-----------------------------5分（2）在Rt△BCH中，BC=CH÷sin∠CBA=4.2÷sin37°≈4.2÷0.6=7千米，---6分则AC+BC﹣AB=10+7﹣14.7=2.3千米．----------------------------------7分答：公路改直后比原来缩短了2.3千米．---------------------------------8分22.（1）证明：如图， 四边形ABCD是平行四边形，∴∠A=∠C，在△AEH与△CGF中，………3分∴△AEH≌△CGF（SAS）.…………………4分（2） 四边形ABCD是平行四边形，∴AB=CD，AD=BC，∠B=∠D．又 AE=CG，AH=CF，∴BE=DG，BF=DH，在△BEF与△DGH中，∴△BEF≌△DGH（SAS），∴EF=GH．又由（1）知，△AEH≌△CGF，∴EH=GF，∴四边形EFGH是平行四边形，………………………………7分∴HG∥EF，∴∠HGE=∠FEG， EG平分∠HEF，∴∠HEG=∠FEG，∴∠HEG=∠HGE，∴HE=HG，………………………………9分∴四边形EFGH是菱形．………………………………10分23.解：（1） 甲团队人数为x人，乙团队人数不超过50人，∴120﹣x≤50，解得：x≥70．…………………1分①当70≤x≤100时，W=70x+80（120﹣x）=﹣10x+9600；…………………3分②当100＜x＜120时，W=60x+80（120﹣x）=﹣20x+9600．……………5分综上所述，W=．（2） 甲团队人数不超过100人，∴x≤100，W=﹣10x+9600， 70≤x≤100，W随x的增大而减少，∴x=70时，W取最大值，最大值=﹣10×70+9600=8900（元），…………………7分若两团联合购票需120×60=7200（元），∴最多可节约8900﹣7200=1700（元）．…………………9分答：甲、乙两团队联合购票比分别购票最多可节约1700元钱．…………………10分24.证明：⑴ AC为⊙O的直径∴∠AEC=∠BEC=90o 在Rt△BEC中,F为BC中点∴BF=EF=CF∴∠FEC=∠FCE…………………2分又 OE=OC∴∠OEC=∠OCE AC⊥BD∴∠FEO=∠FEC+∠OEC=∠FCE+∠OCE=∠FCO=90o…………………4分∴EF是⊙O的切线.…………………5分⑵①设⊙O半径为r,在Rt△AEC中,∠EAC=60o,AC=2r.OC=r,OA=OE∴∠AOE=∠DOC=60o在Rt△OCD中,OC=r,∠DOC=60o,∴CD=在Rt△ACD中,AD=∴∴r=2…………………8分②由①得r=2,则在Rt△AEC中,EC=,∠EOC=120o由⑴得EF⊥OE, ∠ECF=∠EAC=60o∴△EFC为正△…………………9分∴FE=FC=EC=∴S阴=S四边形FEOC-S扇形OEC=2SRt△EFO-S扇形OEC…………………11分=…………………12分25.解：（1）AG=CE与AG⊥CE均成立． 四...