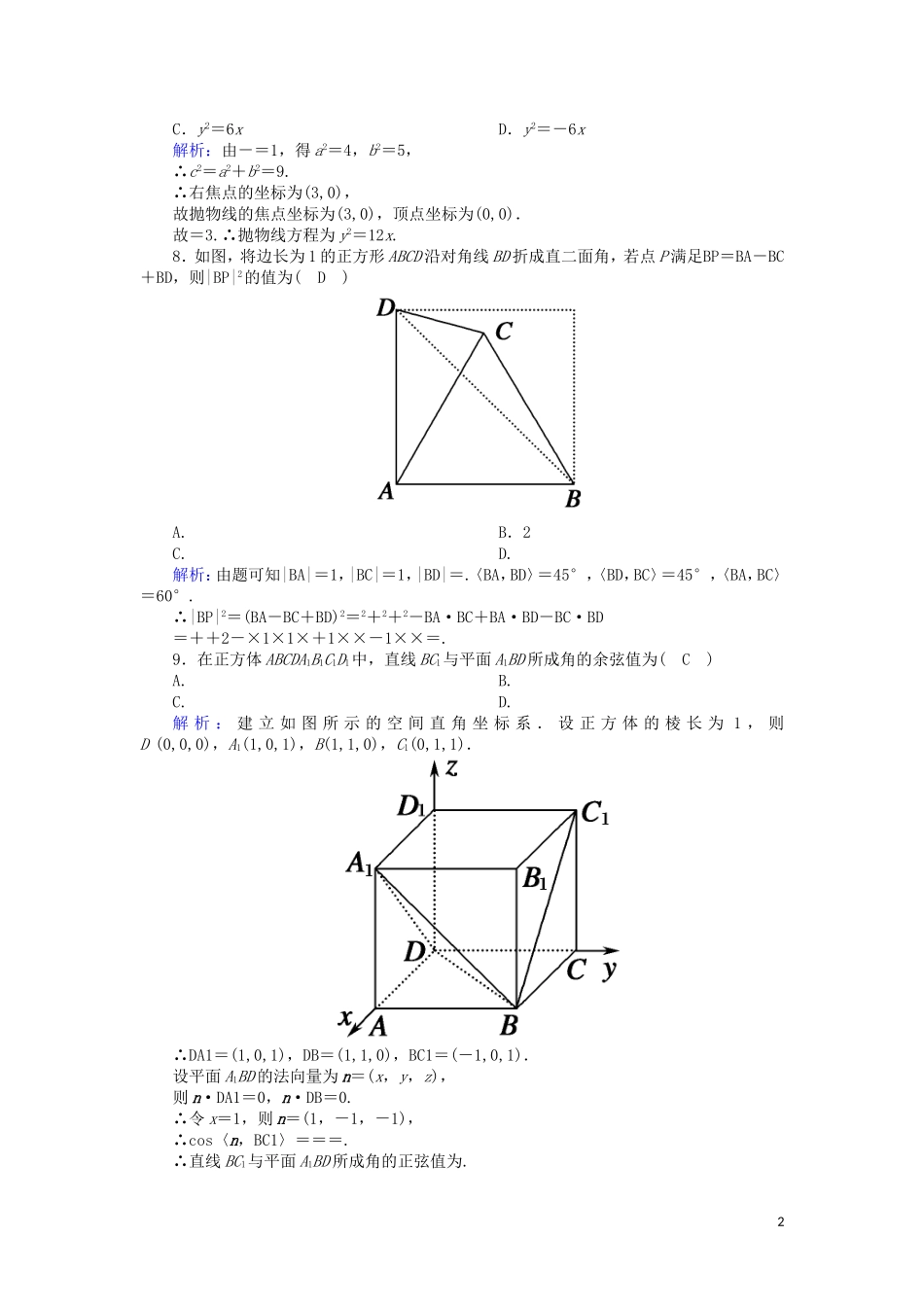
模块综合测试时间:90分钟分值:150分第Ⅰ卷(选择题,共60分)一、选择题(每小题5分,共60分)1.下列四个命题中,既是特称命题又是真命题的是(B)A.任意m∈R,使函数f(x)=x2+mx(x∈R)都是奇函数B.至少有一个实数x0,使得x>0C.全等的三角形必相似D.存在一个负数x,使>2解析:A中,命题是全称命题,且找不到m使f(x)是奇函数,故不合题意;B中,命题是特称命题,且任取一个非零常数代入,不难发现命题正确;C中,命题是省掉全称量词的全称命题,不合题意;D中,对于任意一个负数x,都有<0,所以D是假命题,不合题意.2.命题“对任意的x∈R,x3-x2+1≤0”的否定是(D)A.不存在x∈R,x3-x2+1≤0B.存在x∈R,x3-x2+1≤0C.对任意的x∈R,x3-x2+1>0D.存在x∈R,x3-x2+1>0解析:含有量词的命题的否定,一是要改变相应的量词,二是要否定结论.3.已知条件p:|x-1|<2,条件q:x2-5x-6<0,则p是q的(B)A.充要条件B.充分而不必要条件C.必要而不充分条件D.既不充分又不必要条件解析:命题p:-13D.35-k>0,解得40,b>0),过双曲线P的右焦点,且倾斜角为的直线与双曲线P交于A,B两点,O是坐标原点,若∠AOB=∠OAB,则双曲线P的离心率为(C)A.B.C.D.解析:由题意可知AB是通径,根据双曲线的对称性和∠AOB=∠OAB可知三角形AOB为等边三角形,即÷c=tan=,所以b2=ac,由c2=a2+b2得c2=a2+ac,两边同除以a2得e2-e-1=0,解得e=或e=(舍去).11.已知圆A:(x+3)2+y2=100,圆A内一定点B(3,0),动圆P过B点且与圆A内切,设动圆P的半径为r,则圆心P的轨迹方程是(B)A.+=1B.+=1C.-=1D.-=1解析:如图所示,由题意知|PB|=r, 圆P与圆A内切,圆A的半径为10,∴两圆的圆心距|PA|=10-r,即|PA|+|PB|=10>|AB|=6,∴点P的轨迹是以A、B两点为焦点的椭圆.∴2a=10,2c=|AB|=6.∴a=5,c=3.∴b2=a2-c2=25-9=16,即点P的轨迹方程为+=1.12.已知椭圆M:+=1(a>b>0)的一个焦点为F(1,0),离心率为,过点F的动直线交M于A,B两点,若x轴上的点P(t,0)使得∠APO=∠BPO总成立(O为坐标原点),则t等于(B)A.-2B.2C.-D.解...