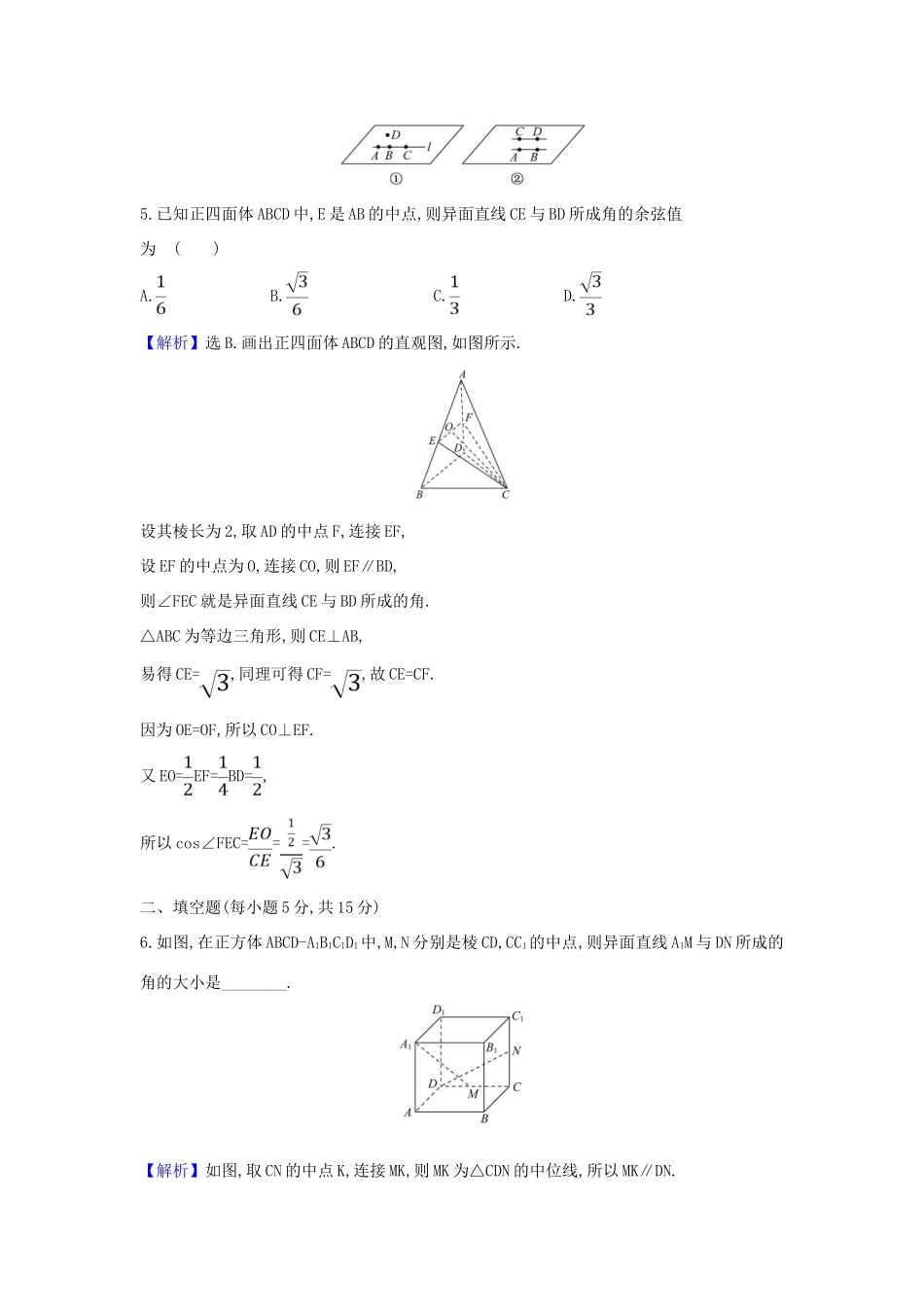
核心素养测评三十九平面的基本性质及两直线位置关系(30分钟60分)一、选择题(每小题5分,共25分)1.在下列命题中,不是公理的是()A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点,有且只有一个平面C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线【解析】选A.选项A是面面平行的性质定理,是由公理推证出来的,而公理是不需要证明的.2.若直线a,b,c满足a∥b,a,c异面,则b与c()A.一定是异面直线B.一定是相交直线C.不可能是平行直线D.不可能是相交直线【解析】选C.若a∥b,a,c是异面直线,那么b与c不可能平行,否则由公理4知a∥c.3.空间四边形ABCD中,E,F分别为AC,BD的中点,若CD=2AB,EF⊥AB,则EF与CD所成的角为()A.30°B.45°C.60°D.90°【解析】选A.取AD的中点H,连接FH,EH,在△EFH中,∠EFH=90°,HE=2HF,从而∠FEH=30°,即EF与CD所成角为30°.4.空间四点A,B,C,D共面而不共线,那么这四点中()A.必有三点共线B.必有三点不共线C.至少有三点共线D.不可能有三点共线【解析】选B.如图①②所示,A,C,D均不正确,只有B正确.5.已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为()A.B.C.D.【解析】选B.画出正四面体ABCD的直观图,如图所示.设其棱长为2,取AD的中点F,连接EF,设EF的中点为O,连接CO,则EF∥BD,则∠FEC就是异面直线CE与BD所成的角.△ABC为等边三角形,则CE⊥AB,易得CE=,同理可得CF=,故CE=CF.因为OE=OF,所以CO⊥EF.又EO=EF=BD=,所以cos∠FEC===.二、填空题(每小题5分,共15分)6.如图,在正方体ABCD-A1B1C1D1中,M,N分别是棱CD,CC1的中点,则异面直线A1M与DN所成的角的大小是________.【解析】如图,取CN的中点K,连接MK,则MK为△CDN的中位线,所以MK∥DN.所以∠A1MK为异面直线A1M与DN所成的角.连接A1C1,AM.设正方体的棱长为4,则A1K==,MK=DN==,A1M==6,所以A1M2+MK2=A1K2,所以∠A1MK=90°.答案:90°7.如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为________.【解析】EF与正方体左、右两侧面均平行.所以与EF相交的侧面有4个.答案:48.设a,b,c是空间中的三条直线,下面给出五个命题:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a∥c;③若a与b相交,b与c相交,则a与c相交;④若a⊂平面α,b⊂平面β,则a,b一定是异面直线;⑤若a,b与c成等角,则a∥b.上述命题中正确的命题是________(只填序号).【解析】由公理4知①正确;当a⊥b,b⊥c时,a与c可以相交、平行,也可以异面,故②不正确;当a与b相交,b与c相交时,a与c可以相交、平行,也可以异面,故③不正确;a⊂α,b⊂β,并不能说明a与b“不同在任何一个平面内”,故④不正确;当a,b与c成等角时,a与b可以相交、平行,也可以异面,故⑤不正确.答案:①三、解答题(每小题10分,共20分)9.如图所示,A是△BCD所在平面外的一点,E,F分别是BC,AD的中点.(1)求证:直线EF与BD是异面直线;(2)若AC⊥BD,AC=BD,求EF与BD所成的角.【解析】(1)假设EF与BD不是异面直线,则EF与BD共面,从而DF与BE共面,即AD与BC共面,所以A,B,C,D在同一平面内,这与A是△BCD所在平面外的一点相矛盾.故直线EF与BD是异面直线.(2)取CD的中点G,连接EG,FG,则AC∥FG,EG∥BD,所以相交直线EF与EG所成的角,即为异面直线EF与BD所成的角.又因为AC⊥BD,则FG⊥EG.在Rt△EGF中,由EG=FG=AC,求得∠FEG=45°,即异面直线EF与BD所成的角为45°.10.已知空间四边形ABCD的对角线AC=20,BD=19,异面直线AC与BD所成的角的余弦值为,点P,Q,M,N分别是AB,BC,CD,DA的中点,(1)求证:四边形PQMN是平行四边形.(2)求四边形PQMN的面积.【解析】(1)因为P,Q是AB,BC的中点,所以PQ∥AC,PQ=AC,同理MN∥AC,MN=AC,所以PQ∥MN,PQ=MN,所以PQMN是平行四边形.(2)因为P,N是AB,AD的中点,所以PN∥BD,PN=BD=,又因为PQ∥AC,所以PQ与PN所成的角就是异面直线AC,BD成的角,所以sin∠QPN===,所以四边形PQMN的面积为S=PQ·PN·sin∠QPN=10××=5.(15分钟35分)1.(5分)设A,B,C,D是空间四个不同的点,在下列命题中,不正确的是()A.若AC与BD共面,则AD与BC共面B.若AC与BD是异面直线,则AD与BC是异面直线C.若...