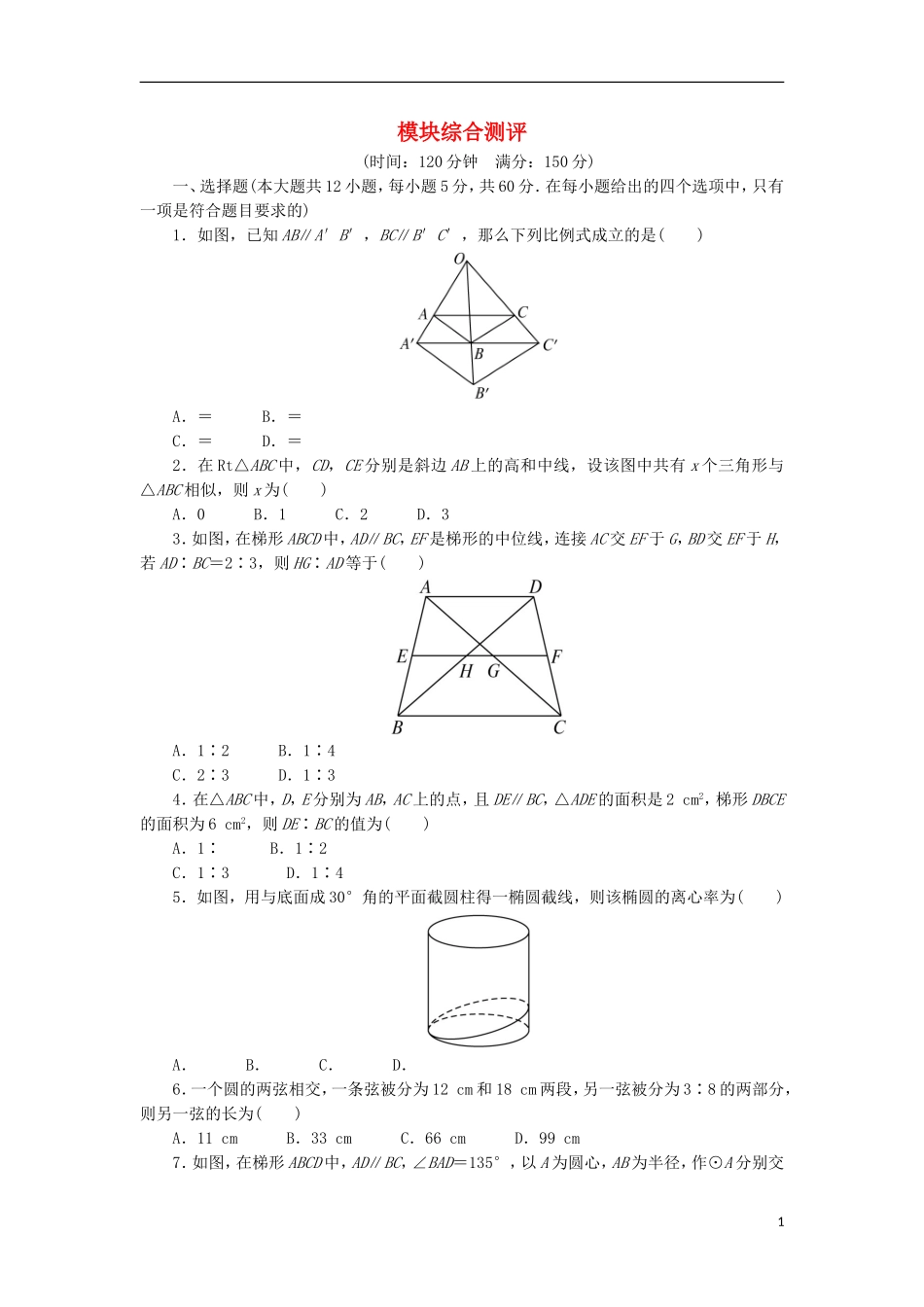
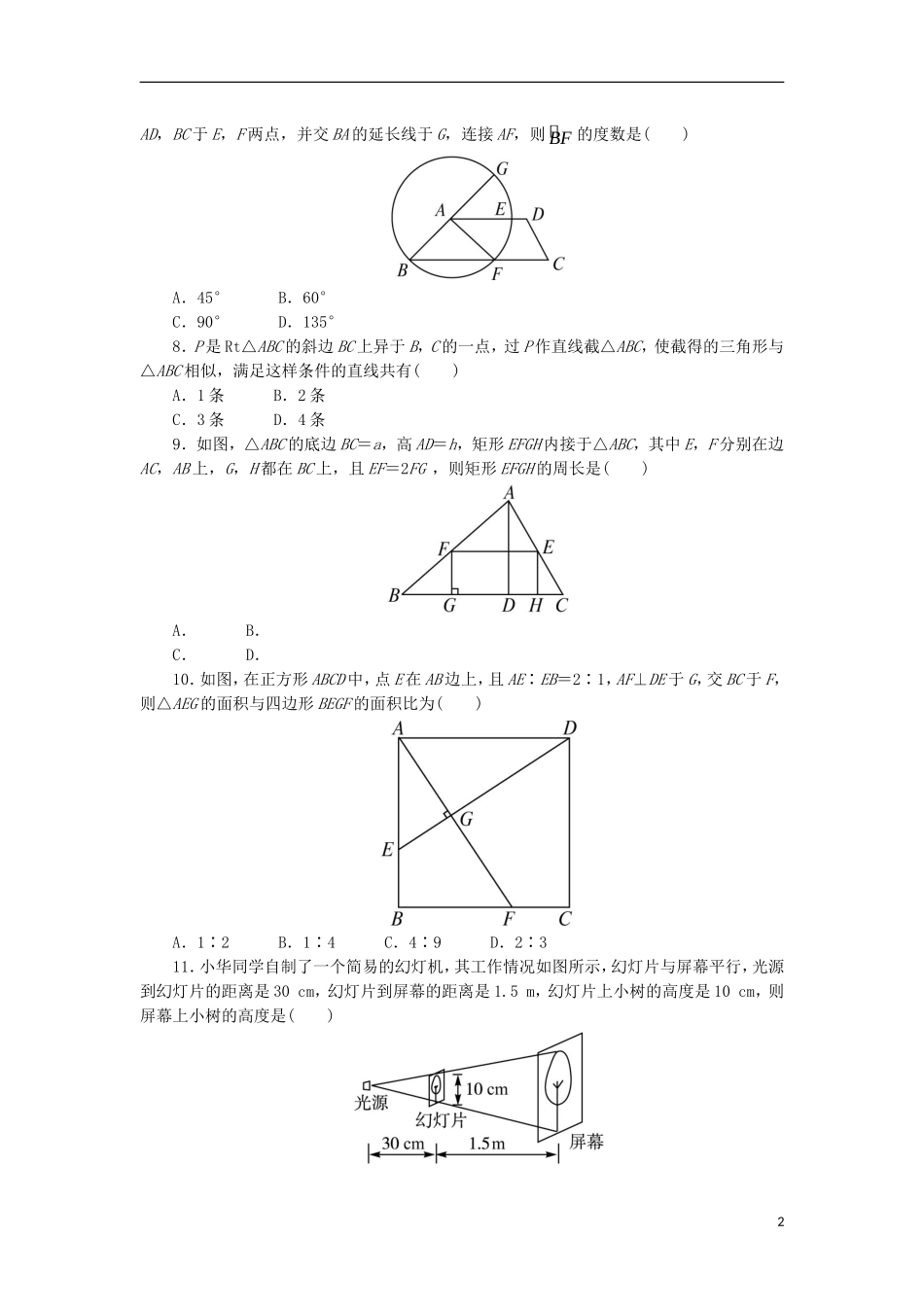
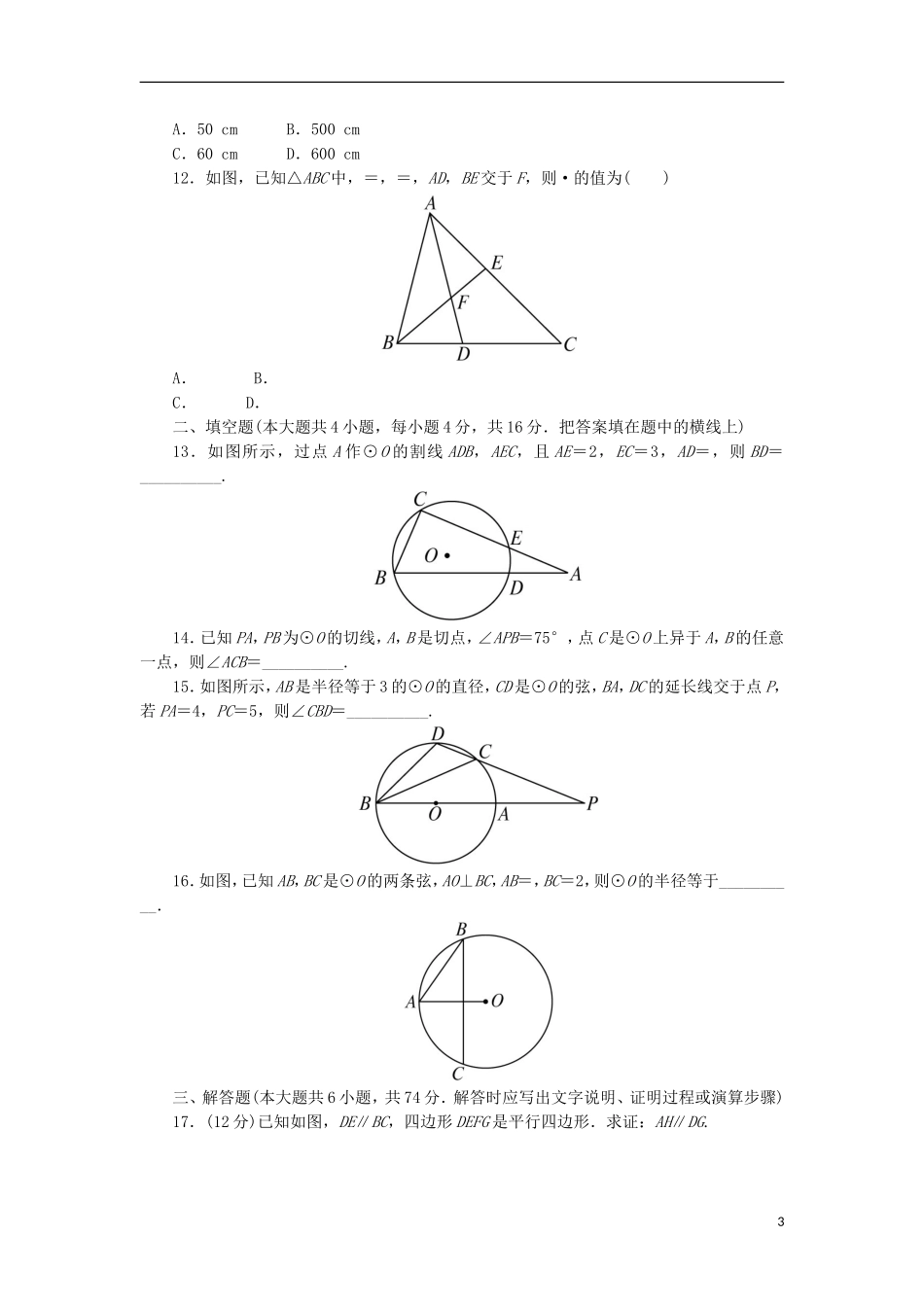
模块综合测评(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,已知AB∥A′B′,BC∥B′C′,那么下列比例式成立的是()A.=B.=C.=D.=2.在Rt△ABC中,CD,CE分别是斜边AB上的高和中线,设该图中共有x个三角形与△ABC相似,则x为()A.0B.1C.2D.33.如图,在梯形ABCD中,AD∥BC,EF是梯形的中位线,连接AC交EF于G,BD交EF于H,若AD∶BC=2∶3,则HG∶AD等于()A.1∶2B.1∶4C.2∶3D.1∶34.在△ABC中,D,E分别为AB,AC上的点,且DE∥BC,△ADE的面积是2cm2,梯形DBCE的面积为6cm2,则DE∶BC的值为()A.1∶B.1∶2C.1∶3D.1∶45.如图,用与底面成30°角的平面截圆柱得一椭圆截线,则该椭圆的离心率为()A.B.C.D.6.一个圆的两弦相交,一条弦被分为12cm和18cm两段,另一弦被分为3∶8的两部分,则另一弦的长为()A.11cmB.33cmC.66cmD.99cm7.如图,在梯形ABCD中,AD∥BC,∠BAD=135°,以A为圆心,AB为半径,作⊙A分别交1AD,BC于E,F两点,并交BA的延长线于G,连接AF,则BF的度数是()A.45°B.60°C.90°D.135°8.P是Rt△ABC的斜边BC上异于B,C的一点,过P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有()A.1条B.2条C.3条D.4条9.如图,△ABC的底边BC=a,高AD=h,矩形EFGH内接于△ABC,其中E,F分别在边AC,AB上,G,H都在BC上,且EF=2FG,则矩形EFGH的周长是()A.B.C.D.10.如图,在正方形ABCD中,点E在AB边上,且AE∶EB=2∶1,AF⊥DE于G,交BC于F,则△AEG的面积与四边形BEGF的面积比为()A.1∶2B.1∶4C.4∶9D.2∶311.小华同学自制了一个简易的幻灯机,其工作情况如图所示,幻灯片与屏幕平行,光源到幻灯片的距离是30cm,幻灯片到屏幕的距离是1.5m,幻灯片上小树的高度是10cm,则屏幕上小树的高度是()2A.50cmB.500cmC.60cmD.600cm12.如图,已知△ABC中,=,=,AD,BE交于F,则·的值为()A.B.C.D.二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中的横线上)13.如图所示,过点A作⊙O的割线ADB,AEC,且AE=2,EC=3,AD=,则BD=__________.14.已知PA,PB为⊙O的切线,A,B是切点,∠APB=75°,点C是⊙O上异于A,B的任意一点,则∠ACB=__________.15.如图所示,AB是半径等于3的⊙O的直径,CD是⊙O的弦,BA,DC的延长线交于点P,若PA=4,PC=5,则∠CBD=__________.16.如图,已知AB,BC是⊙O的两条弦,AO⊥BC,AB=,BC=2,则⊙O的半径等于__________.三、解答题(本大题共6小题,共74分.解答时应写出文字说明、证明过程或演算步骤)17.(12分)已知如图,DE∥BC,四边形DEFG是平行四边形.求证:AH∥DG.318.(12分)如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE�=AC�,DE交AB于点F,且AB=2BP=4,求PF的长度.19.(12分)如图,已知△ABC的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.(1)证明B,D,H,E四点共圆;(2)证明CE平分∠DEF.20.(12分)如图,已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB的延长线于F.求证:=.21.(12分)如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.(1)证明:∠D=∠E;4(2)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.22.(14分)如图,已知ABCD是矩形纸片,E是AB上一点,BE∶EA=5∶3,EC=15,把△BCE沿折痕EC翻折,若B点恰好落在AD边上,设这个点为F,(1)求AB,BC的长度各是多少;(2)若⊙O内切于以F,E,B,C为顶点的四边形,求⊙O的面积.5参考答案一、1.解析: AB∥A′B′,∴=,同理=,∴=,∴选项A不成立;==,∴=,∴选项B成立;由于=,∴AC∥A′C′,∴=,∴选项C不成立;==,∴选项D也不成立.答案:B2.解析:共两个,△ACD和△CBD.答案:C3.解析:由EF是梯形的中位线,得EF=(AD+BC),EH=AD,GF=AD,∴HG=BC-AD.又 AD∶BC=2∶3,故HG=AD.答案:B4.解析:由题意知△ADE∽△ABC,利用面积比等于相似比的平方可得...