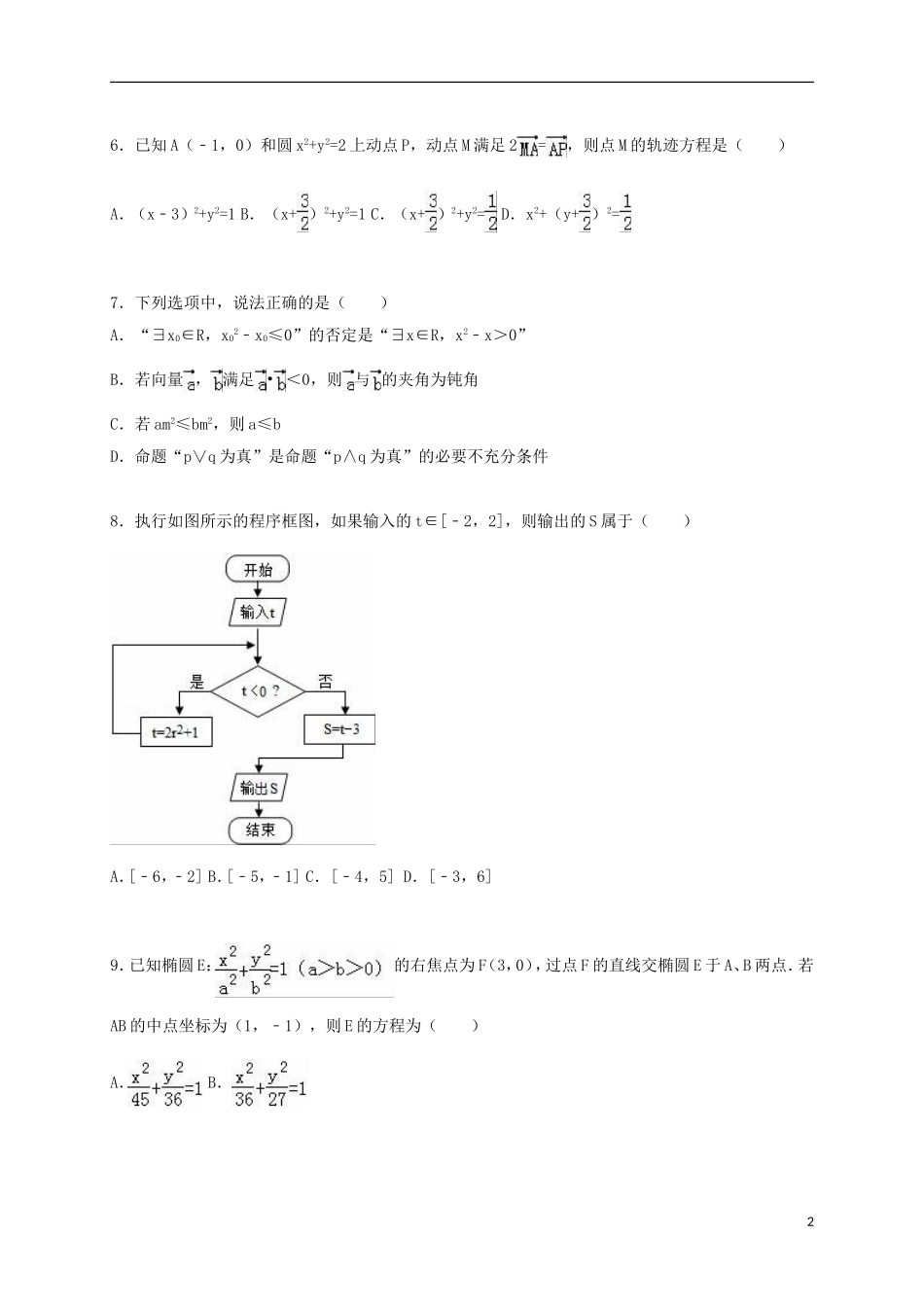
2015-2016学年福建省三明市尤溪一中高二(上)期中数学试卷(理科)一、选择题:(共11小题,每小题5分,共60分)1.已知一组数据为1、5、6、2、6,则这组数据的众数、中位数、平均数的大小关系为()A.中位数>平均数>众数B.众数>中位数>平均数C.众数>平均数>中位数D.平均数>众数>中位数2.设a∈R,则a>1是<1的()条件.A.充分不必要B.必要不充分C.充要D.既不充分也不必要3.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图由图中数据可知身高在[120,130]内的学生人数为()A.20B.25C.30D.354.从装有2个红球和2个黑球的口袋内任取2个球,则恰有一个红球的概率是()A.B.C.D.5.已知P为椭圆上的一点,M,N分别为圆(x+3)2+y2=1和圆(x﹣3)2+y2=4上的点,则|PM|+|PN|的最小值为()A.5B.7C.13D.1516.已知A(﹣1,0)和圆x2+y2=2上动点P,动点M满足2=,则点M的轨迹方程是()A.(x﹣3)2+y2=1B.(x+)2+y2=1C.(x+)2+y2=D.x2+(y+)2=7.下列选项中,说法正确的是()A.“∃x0∈R,x02﹣x0≤0”的否定是“∃x∈R,x2﹣x>0”B.若向量,满足•<0,则与的夹角为钝角C.若am2≤bm2,则a≤bD.命题“p∨q为真”是命题“p∧q为真”的必要不充分条件8.执行如图所示的程序框图,如果输入的t∈[﹣2,2],则输出的S属于()A.[﹣6,﹣2]B.[﹣5,﹣1]C.[﹣4,5]D.[﹣3,6]9.已知椭圆E:的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为()A.B.2C.D.10.已知关于x的二次函数f(x)=ax2﹣4bx+1,设(a,b)是区域,内的随机点,则函数f(x)在区间[1,+∞)上是增函数的概率是()A.B.C.D.11.设P,Q分别为圆x2+(y﹣6)2=2和椭圆+y2=1上的点,则P,Q两点间的最大距离是()A.5B.+C.7+D.6二、填空题:(共4小题,每小题4分,共16分)12.若“x∈[2,5]或x∈{x|x<1或x>4}”是假命题,则x的取值范围是.13.若直线y=kx+1与椭圆恒有公共点,则m的取值范围是:.14.设正项等差数列{an}的前2011项和等于2011,则+的最小值为.15.若以原点为圆心,椭圆的焦半径c为半径的圆与该椭圆有四个交点,则该椭圆的离心率的取值范围为:.三、解答题:(共6小题,第22题14分,其余各题12分,共74分)316.某电视台举办青年歌手大奖赛,有10名评委打分,已知甲、乙两名选手演唱后的打分情况如茎叶图所示:(Ⅰ)从统计的角度,你认为甲与乙比较,演唱水平怎样?(Ⅱ)现场有3名点评嘉宾A、B、C,每位选手可以从中选2位进行指导,若选手选每位点评嘉宾的可能性相等,求甲乙两选手选择的点评嘉宾恰重复一人的概率.17.命题p:实数x满足x2﹣4ax+3a2<0,其中a<0;命题q:实数x满足x2﹣x﹣6≤0或x2+2x﹣8>0;若¬p是¬q的必要不充分条件,求a的取值范围.18.已知椭圆的中心在原点,焦点在x轴上,且长轴为8,离心率为,求:(1)椭圆的标准方程;(2)求椭圆上的点到直线的最大距离.19.已知函数f(x)=x2﹣2ax+1,g(x)=x﹣a,其中a>0,x≠0.(1)对任意x∈[1,2],都有f(x)>g(x)恒成立,求实数a的取值范围;(2)对任意x1∈[﹣2,﹣1],x2∈[2,4],都有f(x1)>g(x2)恒成立,求实数a的取值范围;(3)存在x1∈[﹣2,﹣1],x2∈[2,4],使f(x1)>g(x2)成立,求实数a的取值范围.20.已知数列{an}的前n项和记为Sn,a1=1,an+1=2Sn+1(n≥1).(1)求{an}的通项公式;(2)等差数列{bn}的各项为正,其前n项和为Tn,且T3=15,又a1+b1、a2+b2、a3+b3成等比数列,求Tn;(3)求数列{an•bn}的前n项和.421.已知椭圆C:+=1(a>b>0)的离心率为,其左、右焦点分别为F1,F2,点P(x0,y0)是坐标平面内一点,且x02+y02=.(1)求椭圆C的方程;(2)过点S(0,﹣)且斜率为k的动直线l交椭圆于A、B两点,问:在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出M的坐标和△MAB面积的最大值;若不存在,说明理由.52015-2016学年福建省三明市尤溪一中高二(上)期中数学试卷(理科)参考答案与试题解析一、选择题:(共11小题,每小题5分...