安徽省合肥市高三数学上学期调研性检测试卷 理(PDF) 安徽省合肥市高三数学上学期调研性检测试卷 理(PDF) 安徽省合肥市高三数学上学期调研性检测试卷 理(PDF)VIP免费

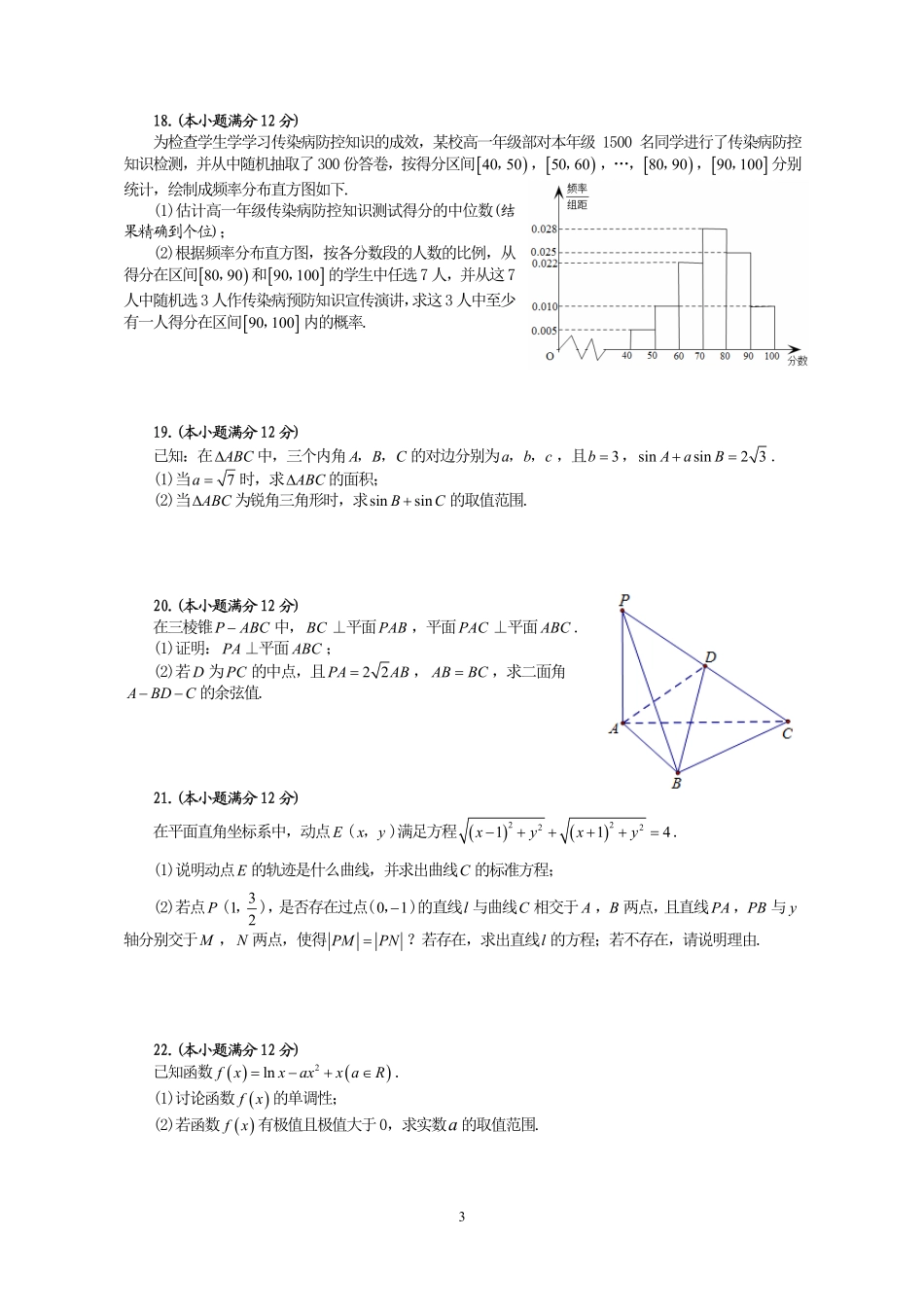
1合肥市2021届高三调研性检测数学试题(理科)(考试时间：120分钟满分：150分)第Ⅰ卷(60分)一、选择题：本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若复数z满足12izi，其中i是虚数单位，则复数z的模为A.2B.3C.22D.32.若集合1Axx，2230Bxxx，则ABA.13，B.13，C.11，D.1，3.若变量xy，满足约束条件1133xyxyxy，，，-则目标函数3zxy的最小值为A.92B.-4C.-3D.14.为了保障广大人民群众的身体健康，在新冠肺炎疫情防控期间，有关部门对辖区内15家药店所销售的A，B两种型号的口罩进行了抽检，每家药店抽检10包口罩(每包10只)，15家药店中抽检的A，B型号口罩不合格数(Ⅰ，Ⅱ)的茎叶图如图所示，则下列描述不正确．．．的是A.估计A型号口罩的合格率小于B型号口罩的合格率B.Ⅰ组数据的众数大于Ⅱ组数据的众数C.Ⅰ组数据的中位数大于Ⅱ组数据的中位数D.Ⅰ组数据的方差大于Ⅱ组数据的方差5.设数列na的前n项和为nS，若3122nnSa，则5SA.81B.121C.243D.3646.函数cosxxxxfxee在，上的图象大致是7.周六晚上，小红和爸爸、妈妈、弟弟一起去看电影，订购的4张电影票恰好在同一排且连在一起.为安全起见，每个核子至少有一侧有家长陪坐，则不同的坐法种数为A.8B.12C.16D.208.已知函数2sinfxx(0，2)的部分图象如图所示，则函数fx的单调递减区间为2A.3[22]88kkkZ，B.3[]88kkkZ，C.37[22]88kkkZ，D.37[]88kkkZ，9.如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该几何体的体积为A.32B.16C.83D.16310.在ABC中，DEF，，分别是边BCCAAB，，的中点，ADBECF，，交于点G，则：①1122EFCABC；②1122BEABBC；③ADBEFC；④0GAGBGC.上述结论中，正确的是A.①②B.②③C.②③④D.①③④11.双曲线2222:1xyCab(00ab，)的左、右焦点分别为12FF，，M为C的渐近线上一点，直线2FM交C于点N，且20FMOM，2232FMFN(O为坐标原点)，则双曲线C的离心率为A.5B.2C.3D.212.已知a，bR，函数321fxaxbxx(0a)恰有两个零点，则ab的取值范围是A.0，B.1，C.14，D.14，第Ⅱ卷(90分)二、填空题：本大题共4小题，每小题5分，满分20分.把答案填写在答题卡上的相应位置.13.若命题p：若直线l与平面内的所有直线都不平行，则直线l与平面不平行；则命题p是命题(填“真”或“假”).14.若直线l经过抛物线24xy的焦点且与圆22121xy相切，则直线l的方程为.15.已知函数cosfxxxxR，，是钝角三角形的两个锐角，则cosfsinf(填写：“＞”或“＜”或“＝”).16.已知三棱锥PABC的顶点P在底面的射影O为ABC的垂心，若2PBCABCOBCSSS，且三棱锥PABC的外接球半径为3，则PABPBCPACSSS的最大值为.三、解答题：解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)设数列na的前n项和为nS，13a，21a.若数列nSn为等差数列.(1)求数列na的通项公式na；(2)设数列11nnaa的前n项和为nT，若对*nN都有nTm成立，求实数m的取值范围.318.(本小题满分12分)为检查学生学学习传染病防控知识的成效，某校高一年级部对本年级1500名同学进行了传染病防控知识检测，并从中随机抽取了300份答卷，按得分区间4050，，5060，，…，8090，，90100，分别统计，绘制成频率分布直方图如下.(1)估计高一年级传染病防控知识测试得分的中位数(结果精确到个位)；(2)根据频率分布直方图，按各分数段的人数的比例，从得分在区间8090，和90100，的学生中任选7人，并从这...