初三数学分式及一元二次方程期中总复习 华东师大版 试题VIP免费

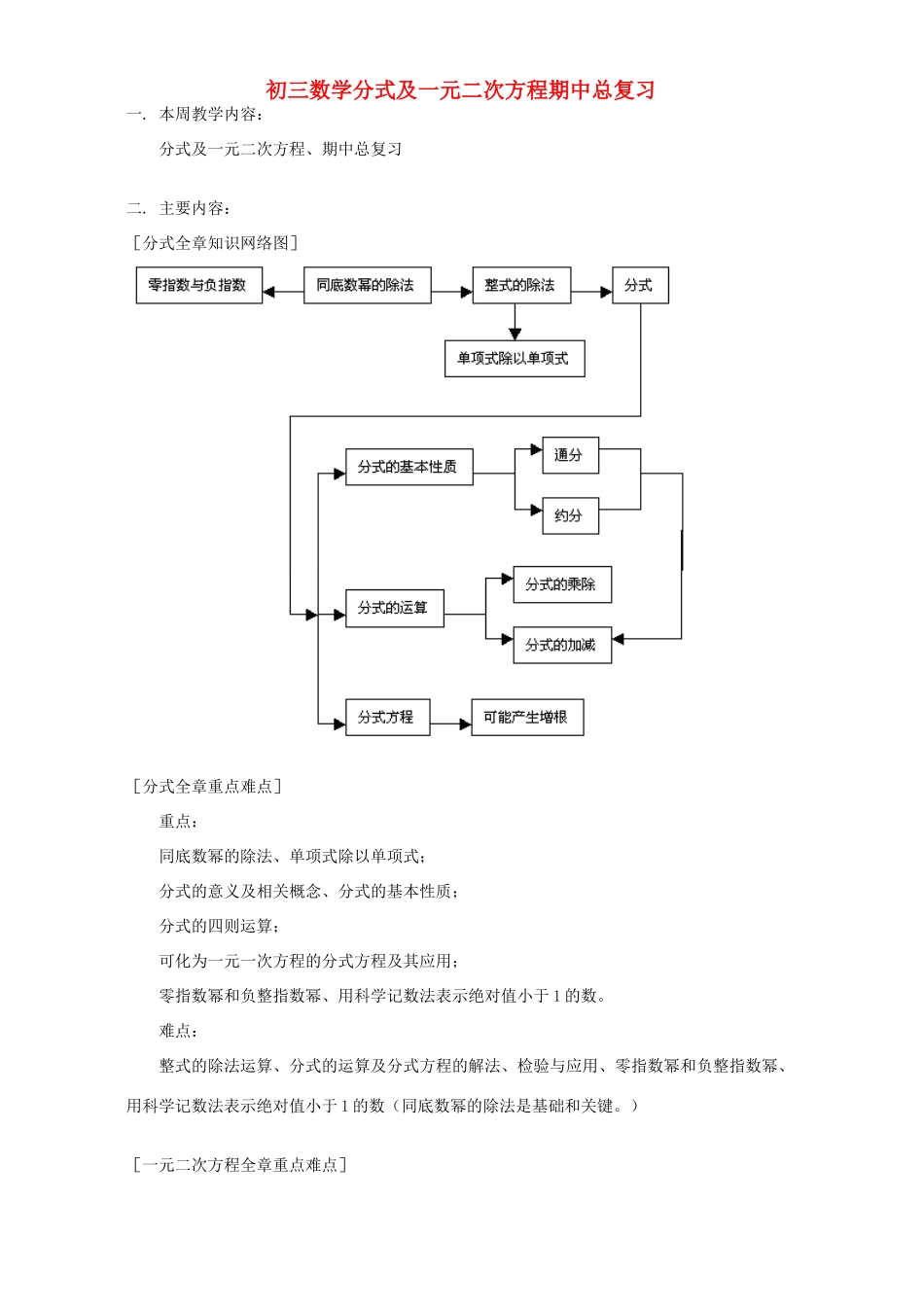
初三数学分式及一元二次方程期中总复习一.本周教学内容：分式及一元二次方程、期中总复习二.主要内容：［分式全章知识网络图］［分式全章重点难点］重点：同底数幂的除法、单项式除以单项式；分式的意义及相关概念、分式的基本性质；分式的四则运算；可化为一元一次方程的分式方程及其应用；零指数幂和负整指数幂、用科学记数法表示绝对值小于1的数。难点：整式的除法运算、分式的运算及分式方程的解法、检验与应用、零指数幂和负整指数幂、用科学记数法表示绝对值小于1的数（同底数幂的除法是基础和关键。）［一元二次方程全章重点难点］重点：一元二次方程的解法；应用一元二次方程，解决实际中的数学问题；一元二次方程根的判别式的应用；难点：灵活地选择解法，求解一元二次方程；运用根的判别式灵活解题；了解并用根与系数关系知识解决较复杂的一元二次方程综合题．［知识精析与典型例题］一.同底数幂的除法运算及应用1.nmnmaaa（nmnma,,,0都是正整数）。2.nmnmaaa（都是正整数nma,,0）。3.),,0()(都是正整数nmaaanmnm。4.121222)()(nnnnaaaa；；（n为正整数）nnnnbabaabba2222)()()()；（；（n为正整数）12121212)()()()(nnnnbabaabba；。（n为正整数）例：已知8,4nmaa，求nma23的值。分析：将指数相减恢复为幂的除法，将指数相乘恢复为幂的乘方。解：18423232323nmnmnmaaaaa二.分式有意义及分式值为零、为正、为负的条件1.分式有意义：分式的分母≠0。2.分式值为0：00分式的分子分式的分母。3.分式在分子、分母同号时值为正；分式在分子、分母异号时值为负。例1：求使下列各分式无意义的字母的值：（1）132aa（2）213xxx分析：使分式无意义的条件为分母＝0，则只求分母＝0时的字母的取值即可。解：（1）由012a即得a＝±1时，分式无意义。（2）由012xx即01xx2得251x时，分式无意义。例2：当a取何值时，下列各分式值为0：（1）163aa（2）242aa分析：分式值为0的条件是00分子分母，因此有两个条件限制了字母的取值。解：（1）06301aa∴2a1a∴a＝2时，分式值为0。（2）04022aa∴22aa∴a＝2时，分式值为0。例3：当a取何值时，分式1632aa值为正？分析：分式在分子、分母同号时值为正。解：063012aa则2a时分式值为正；三.分式的运算——约分、通分、加、减、乘除、乘方及混合运算1.分式基本性质：分式的分子和分母都乘以或除以同一个不等于零的整式，分式的值不变。公式：MBMAMBMABA（M是不等于零的整式）。2.分式的乘除法：实质是分式的约分。公式：nambnmabmnabmanbmnab;。3.分式的乘方：把分子、分母各自乘方。公式：nnnbaba，n为正整数。4.分式的加减法：（1）同分母分式相加减，分母不变，分子相加减：cbacbca；（2）异分母分式相加减，先通分化为同分母分式再加减：bdbcadbdbcbdaddcba。5.分式的混合运算：先乘方，再乘除，最后加减，如有括号先算括号内的。在混合运算中要注意优化运算顺序，在法则、定律允许的前提下，尽量先进行乘除最后加减；此外，运算结果应是最简分式或整式。例1：计算：（1）322223bacabcbcacbabac2782784336422（2）964494232222xxxxxxxx；（3）abcbaab5232122（公分母为2210ba）222222221043051041030105baabcbabaabcbabbaa；（4）2123242aaaa（公分母为12aa）)1)(2(1)1)(2(33)1)(2(44aaaaaaaa)1)(2(2aaa；（5）242)4(2)2)(2(21222222222xxxxxxxxxxxxxxx；（6）baababaa2121解法1：aabaababaa22221212原式abaababaa2)(2)(121aababaa2)21)((121aaa22121...