四川省成都市高三数学上学期入学考试试卷 文(PDF)试卷VIP免费

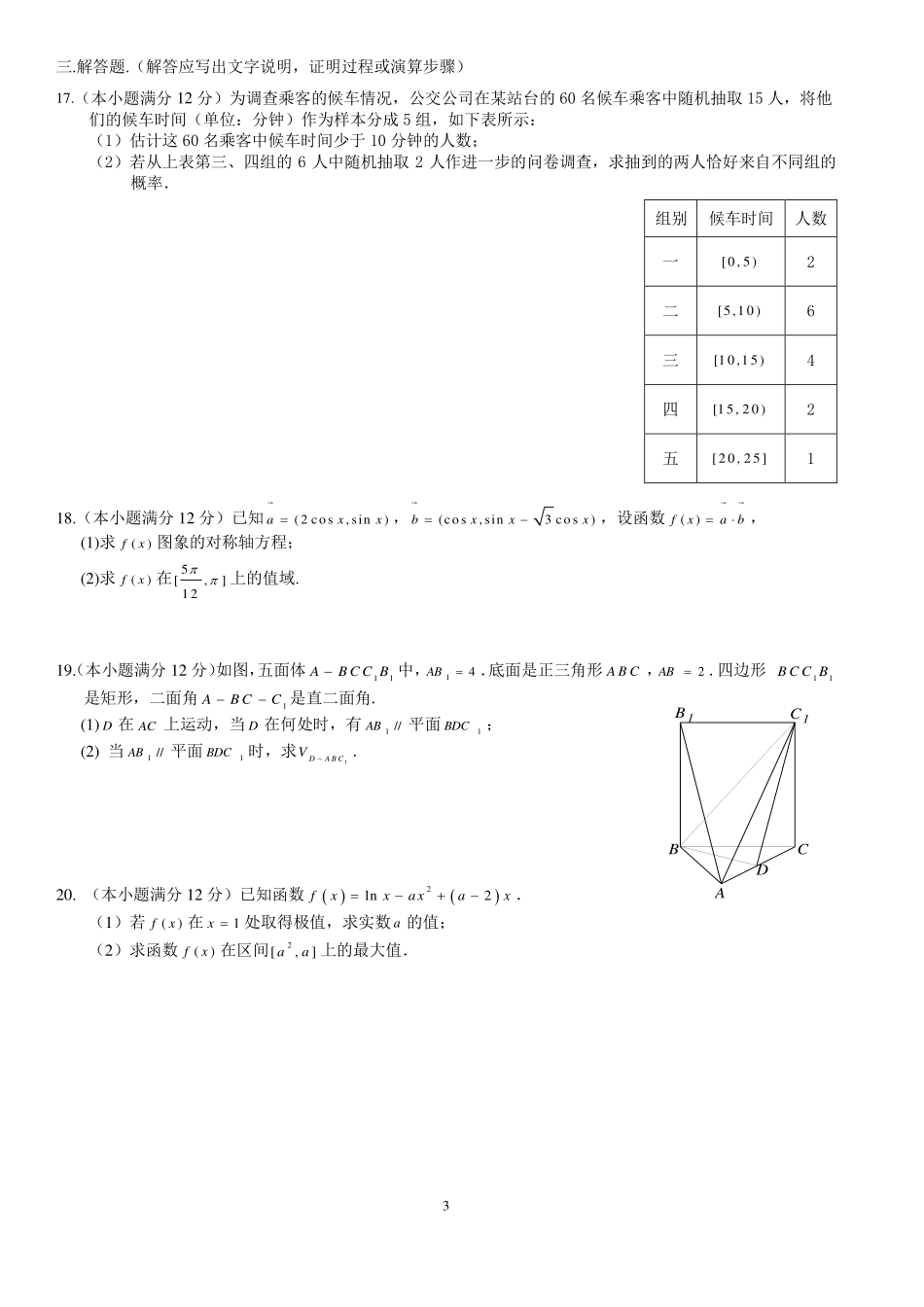
1开始输入x结束0k21xx1kk2015?x是否输出x，k成都七中高三数学入学测试(文)命题人：黄太平祁祖海满分150分考试时间120分钟I卷一.选择题.（本大题共12小题，每题5分，共60分，每小题的四个选项中仅有一项符合题目要求）1.1=ii()A.1iB.1iC.1iD.1i2.sin210()A.12B.12C.32D.323.数列{}na满足111nnaa，112a，则3a()A.12B.2C.1D.14.已知集合|1,|21,xAxxBx则AB()A.(0,1)B.(-1,1)C.10,2D.(-1,0)5.从区间[0,]2内随机取一个实数x，则3sin2x的概率为()A.32B.23C.12D.136.已知命题p:函数()fxxa在,1上是单调函数,命题q:函数()log(1)(0agxxa且1)a在1,上是增函数,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.按右图所示的程序框图运算，若输入200x，则输出k的值是（）A．3B．4C．5D．68.设不等式组110xyxyy表示的平面区域为D,若直线3ykx与平面区域D有公共点,则k的取值范围为()A.3,3B.11,,33C.,33,D.11,3329.一个几何体的三视图如图所示,则该几何体的体积为()A.163B.203C.152D.13210.若两个非零向量,ab满足2,ababa则向量ab与ab的夹角是()A.6B.3C.23D.5611.已知,AB为双曲线E的左,右顶点,点M在E上,ABM为等腰三角形,且顶角为0120,则E的离心率为()A.5B.2C.3D.212.若02bab，当1()(2)aabab取最小值时，ab()A.4B.5C.6D.7二.填空题.（本大题共4小题，每题5分，共20分）13.设函数4()fxxax，若曲线()yfx在1x处的切线斜率为1，那么a.14.已知ABC中，A、B、C的对边分别为abc、、，且2223abcbc，则A.15.设,,为互不重合的三个平面,l为直线,给出下列命题:(1)若//,,则;(2)若,且l,则l;(3)若直线l与平面内的无数条直线垂直,则直线l与平面垂直;(4)若内存在不共线的三点到的距离相等,则平面平行于平面.其中真命题的序号为(写出所有真命题的序号).16.已知函数(fx）为偶函数，又在区间[0,2]上有235,01()222,12xxxxxfxx,若()()Fxfxa在区间[2,2]上恰好有4个零点,则a的取值范围是.111111正视图侧视图俯视图3三.解答题.（解答应写出文字说明，证明过程或演算步骤）17.（本小题满分12分）为调查乘客的候车情况，公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间（单位：分钟）作为样本分成5组，如下表所示：（1）估计这60名乘客中候车时间少于10分钟的人数；（2）若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查，求抽到的两人恰好来自不同组的概率．18.（本小题满分12分）已知(2cos,sin)axx，(cos,sin3cos)bxxx，设函数()fxab，(1)求()fx图象的对称轴方程；(2)求()fx在5[,]12上的值域.19.（本小题满分12分）如图，五面体11ABCCB中，41AB．底面是正三角形ABC，2AB.四边形11BCCB是矩形，二面角1ABCC是直二面角.(1)D在AC上运动，当D在何处时，有//1AB平面1BDC；(2)当//1AB平面1BDC时，求1DABCV.20.（本小题满分12分）已知函数2ln2fxxaxax．（1）若()fx在1x处取得极值，求实数a的值；（2）求函数()fx在区间2[,]aa上的最大值．组别候车时间人数一[0,5)2二[5,10)6三[10,15)4四[15,20)2五[20,25]1C1B1DCBA421.（本小题满分12分）如图，O为坐标原点，A和B分别是椭圆1C：22221(0)xyabab和2C：22221(0)xymnmn的动点，满足0OAOB，且椭圆1C的离心率为22.当动点A在x轴上的投影恰为1C的右焦点F时，有24AOFS.(1)求椭圆1C的标准方程；(2)若1C与2C共焦点，且1C的长轴与2C的短轴等长，求2||AB的取值范围.请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分.22.（本小题满分10分）(选修4-4:坐标系与参数方程)已知在平面直角坐标系xOy中,直线l的参数方程是222422xtyt（t是参数）,以...