3.1.3导数的几何意义VIP免费

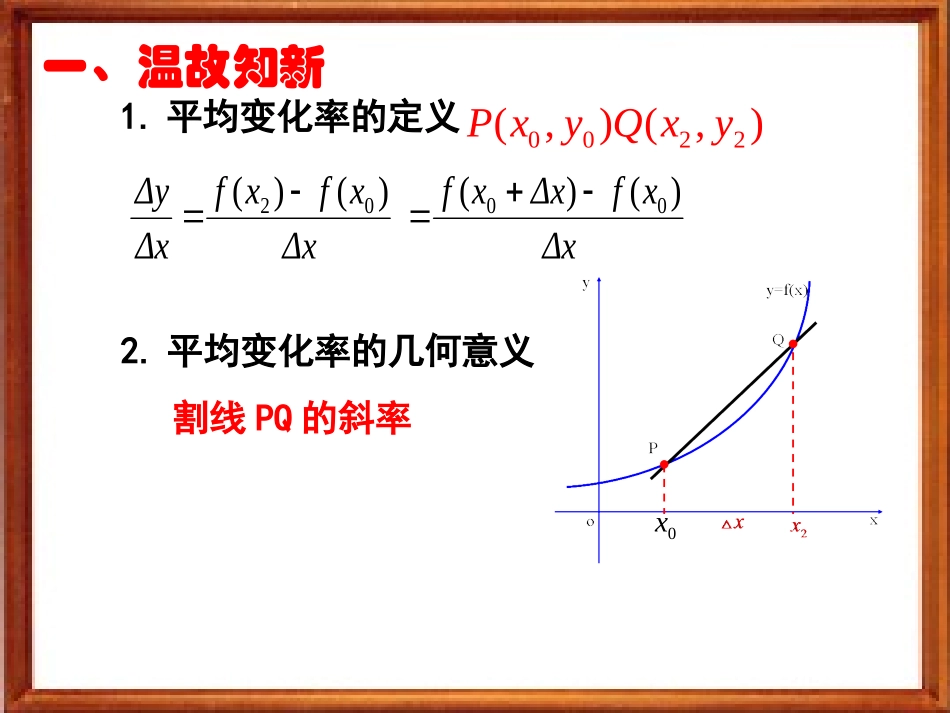
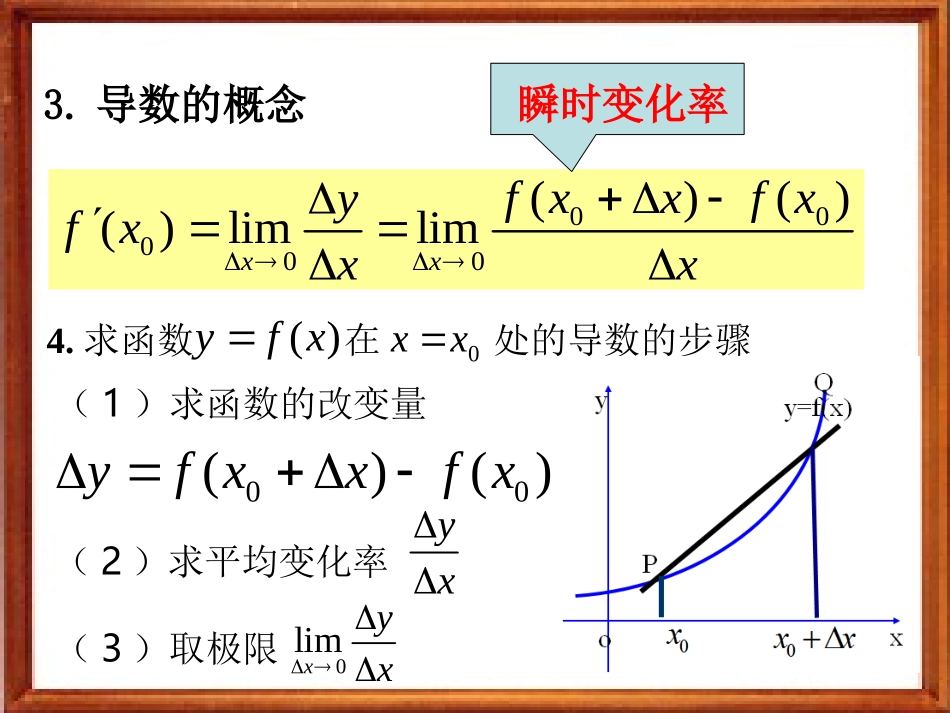
1.平均变化率的定义一、温故知新2.平均变化率的几何意义割线PQ的斜率0022(,)(,)PxyQxyΔxxfxfΔxΔy)()(02ΔxxfΔxxf)()(000x3.导数的概念00000()()()limlimxxfxxfxyfxxx)(xfy0xx4.求函数在处的导数的步骤（1）求函数的改变量（2）求平均变化率（3）取极限00()()yfxxfxyx0limxyx瞬时变化率P二、引入同学们回顾初中所学圆的切线动手画圆及过圆上一点P作圆的割线和切线Q切线：直线与圆只有一个公共点割线：直线与圆有两个公共点二、引入问题1：直线是否为点A处的切线？1l问题2：直线是否为点B处的切线？2l问题3：直线是否为点C处的切线？2l几何画板PP1oxyy=f(x)割线切线T三、切线的定义0xΔx0+xx动画展示P2P3P4我们发现,当点Q沿着曲线无限接近点P，Δx→0时,割线PQ趋近于确定的位置，这个确定位置的直线PT称为曲线在点P处的切线.?nPPPTk探究：割线的斜率与切线的斜率有什么关系呢000limxfxxfxkx四、导数的几何意义形：nPPyo)(xfyP相切相交nP数：nPP割线切线0x割线斜率切线斜率0=()kfx切线即0000()()(,())yfxxxfxPxfx函数在处的导数，就是曲线在点处的切线的斜率P四、导数的几何意义（1）若曲线y=f(x)在点P(x0,f(x0))处的切线方程为2x+y+1=0，则.)(0xf小试牛刀(2)5-1,________yfxfPk数图图则线点处线函＝的象如所示，已知＝曲在的切斜率．21探究：观察图像，割线PP1、PP2、PP3、PP4、切线PT哪一条在点P处附近更贴近函数曲线？几何画板五、以直代曲PP1oxyy=f(x)割线切线T0xΔx0+xxP2P3P4结论：过点P处的切线PT最贴近点P处的曲线f（x）所以，在点P附近，曲线就可以用过点P的切线PT近似代替以直代曲)(0xf切线k0x曲线在附近的变化情况0x在附近切线的变化情况近似代替五、以直代曲PPP例1如图,它表示跳水运动中高度随时间变化的函数105.69.4)(2ttth的图象.根据图象,请描述、比较曲线在附近的变化情况.210,,ttt)(th解:可用曲线h(t)在t0,t1,t2处的切线刻画曲线h(t)在上述三个时刻附近的变化情况.(1)当t=t0时,曲线h(t)在t0处的切线l0平行于x轴.故在t=t0附近曲线比较平坦,几乎没有升降.(2)当t=t1时,曲线h(t)在t1处的切线l1的斜率h’(t1)<0.故在t=t1附近曲线下降,即函数h(t)在t=t1附近单调递减.tohl0t0t1l1t2l2t4t3(3)当t=t2时,曲线h(t)在t2处的切线l2的斜率h’(t2)<0.故在t=t2附近曲线下降,即函数h(t)在t=t2附近也单调递减.从图可以看出,直线l1的倾斜程度小于直线l2的倾斜程度，这说明h(t)曲线在l1附近比在l2附近下降得缓慢。toht4t3根据图像描述函数在附近增（减）以及增（减）快慢的情况)(th34,tt。数在两点附近单调递增点附近曲线上升，即函，所以在两斜率均大于处的切线的、函数在0tt43附近上升的快速附近比在这说明曲线在处切线的倾斜程度，处切线的倾斜程度大于但是4343tttt0BxAxxyBA1()()()AByfxfxfx、已知函数的图象如图所示则与的大小关系是)()(.BAxfxfA)()(.BAxfxfB)()(.BAxfxfC不能确定.D牛刀小试B例2:22(1)yx切线方程：20xy即：求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.:(1)(1)yfxf解22=(1)1(11)=2()xxx所以在点P(1,2)处的切线斜率0()2kfx000:()limlim(2=2xxyfxxx解）22()2yxxxxx（1）求出函数在点x0处的导数，得到曲线在点(x0,f(x0))的切线的斜率。)(0xf（2）根据直线方程的点斜式写出切线方程，即).)(()(000xxxfxfy归纳:求切线方程的步骤2、求切线方程的步骤：1、导数的几何意义：3、函数在点P附近的增减性1、极限逼近思想2、数形结合思想3、以直代曲思想方法2、观察、实验1、类比、猜想3、由特殊到一般4、分析法4、转化思想若研究函数在某个区间内的变化趋势应该怎么办？）处的切线方程是在点（、曲线1,13xy处的切线斜率为在点、曲线)8,2(2)(22Axxf课后作业1、习题3.1A组第5题实践作业：收集有关微积分创立的时代背景和牛顿、莱布尼兹的资料；搜集数学史上、实际生活中、身边的有关“以直代曲”的事例