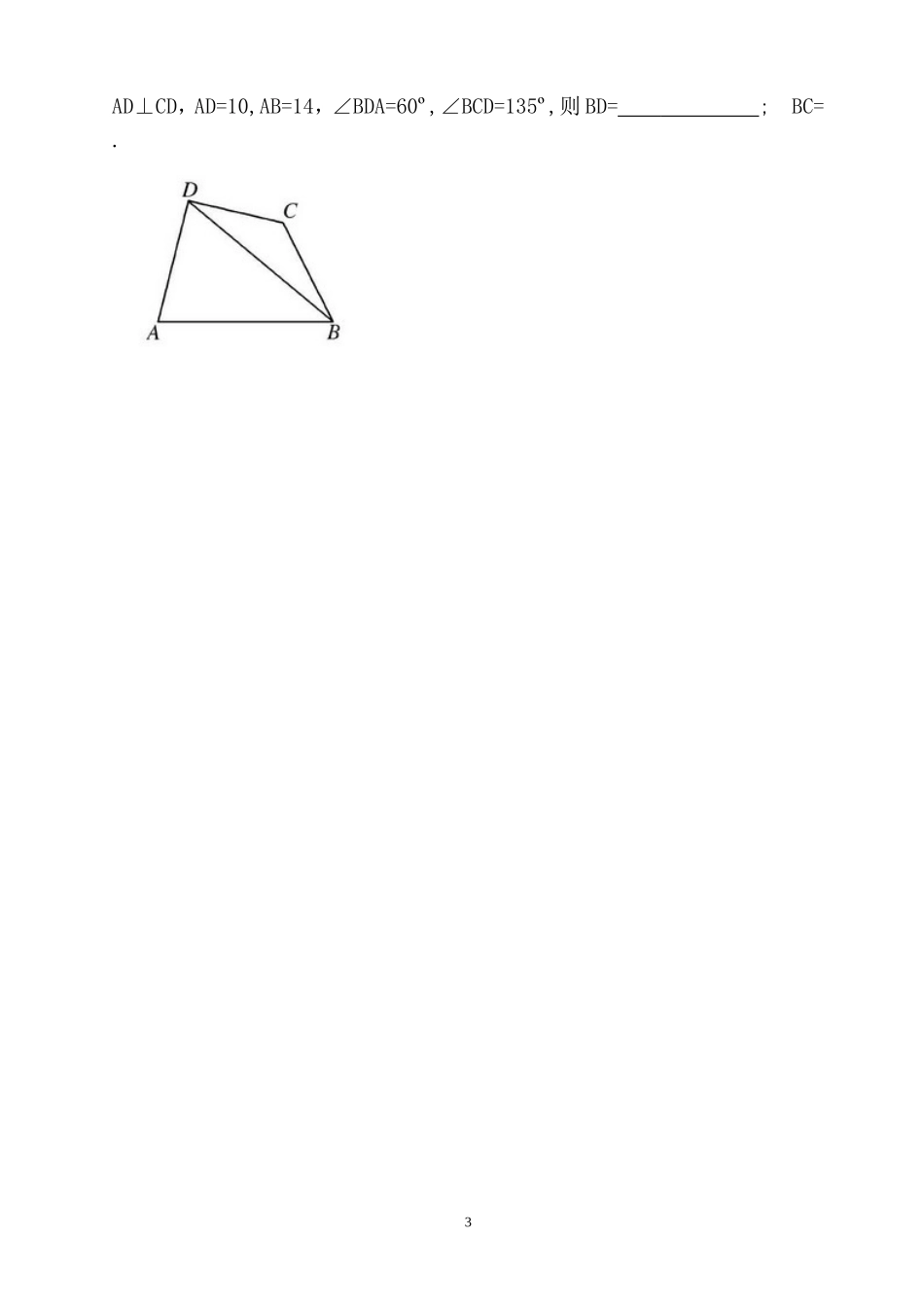
正、余弦定理在解三角形中的应用【学习目标要求】1、识记三角形的有关知识2、正确判断考查题型3、总结相关题型的解题方法与技巧4、规范答题过程.【重难点】三角形中的边角互化、以平面图形为背景的解三角形问题.知识梳理:定理正弦定理余弦定理内容===2R.(R为△ABC外接圆半径)a2=b2+c2-2bc·cos_A;b2=c2+a2-2ca·cos_B;c2=a2+b2-2ab·cos_C变形形式(1)a=2RsinA,b=2RsinB,c=2RsinC;(2)sinA=,sinB=,sinC=cosA=;cosB=;cosC=课前自主学习1、在△ABC中.若∠B=45º,AC=,cosC=,则BC=.2、△ABC的内角A,B,C的对边分别为a,b,c.已知b+a(sinC-cosC)=0,a=2,c=,求角C.探究一:解三角形中的边角互化问题例1、△ABC的内角A,B,C的对边分别为a,b,c.已知b+a(sinC-cosC)=0,a=2,c=,求角C.例2△ABC的内角A,B,C的对边分别为a,b,c.若2acosC=2b-c,求角A.1解后反思:解三角形的综合问题中关于“边角互化”的处理方法有哪些?探究二:平面图形中解三角形中问题例3、(2018年全国卷Ⅰ)在平面四边形ABCD中,∠ADC=90º,∠A=45º,AB=2,BD=5.(1)求cos∠ADB;(2)若DC=,求BC.例4、(2015年全国卷Ⅰ)在平面四边形ABCD中,∠A=∠B=∠C=75º,BC=2.则AB的取值范围是.【课堂小结】通过本节课的学习,从知识、思想和能力三个方面你有什么收获?【课后巩固】1、△ABC的内角A,B,C的对边分别为a,b,c.若2bcosB=acosC+ccosA,求角B.2、(16年)△ABC的内角A,B,C的对边分别为a,b,c.若cosA=,cosC=,a=1,则b=.3、在△ABC中,B=,BC边上的高等于BC,则cosA=.4、如图,在四边形ABCD中,已知2AD⊥CD,AD=10,AB=14,∠BDA=60º,∠BCD=135º,则BD=;BC=.3