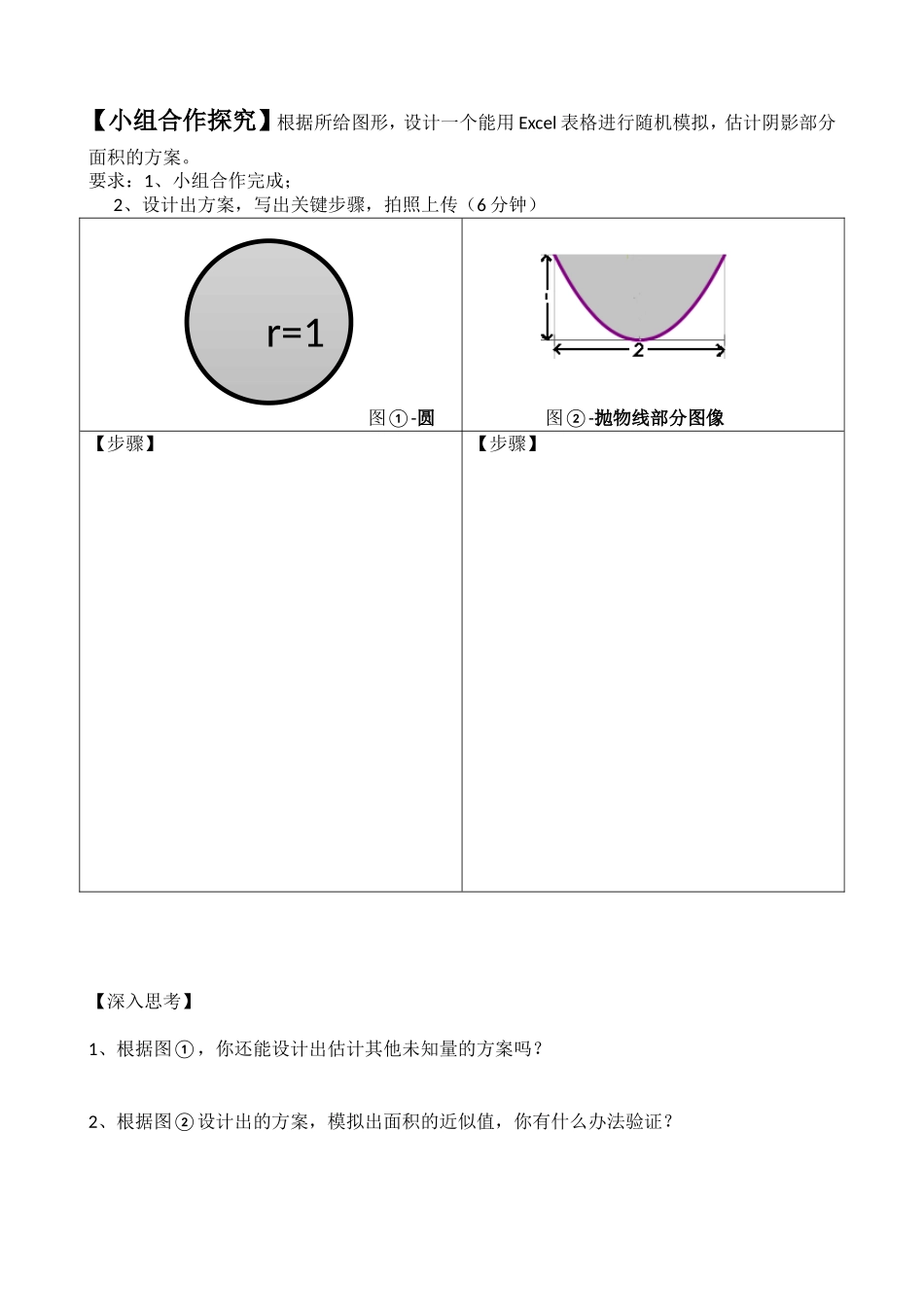
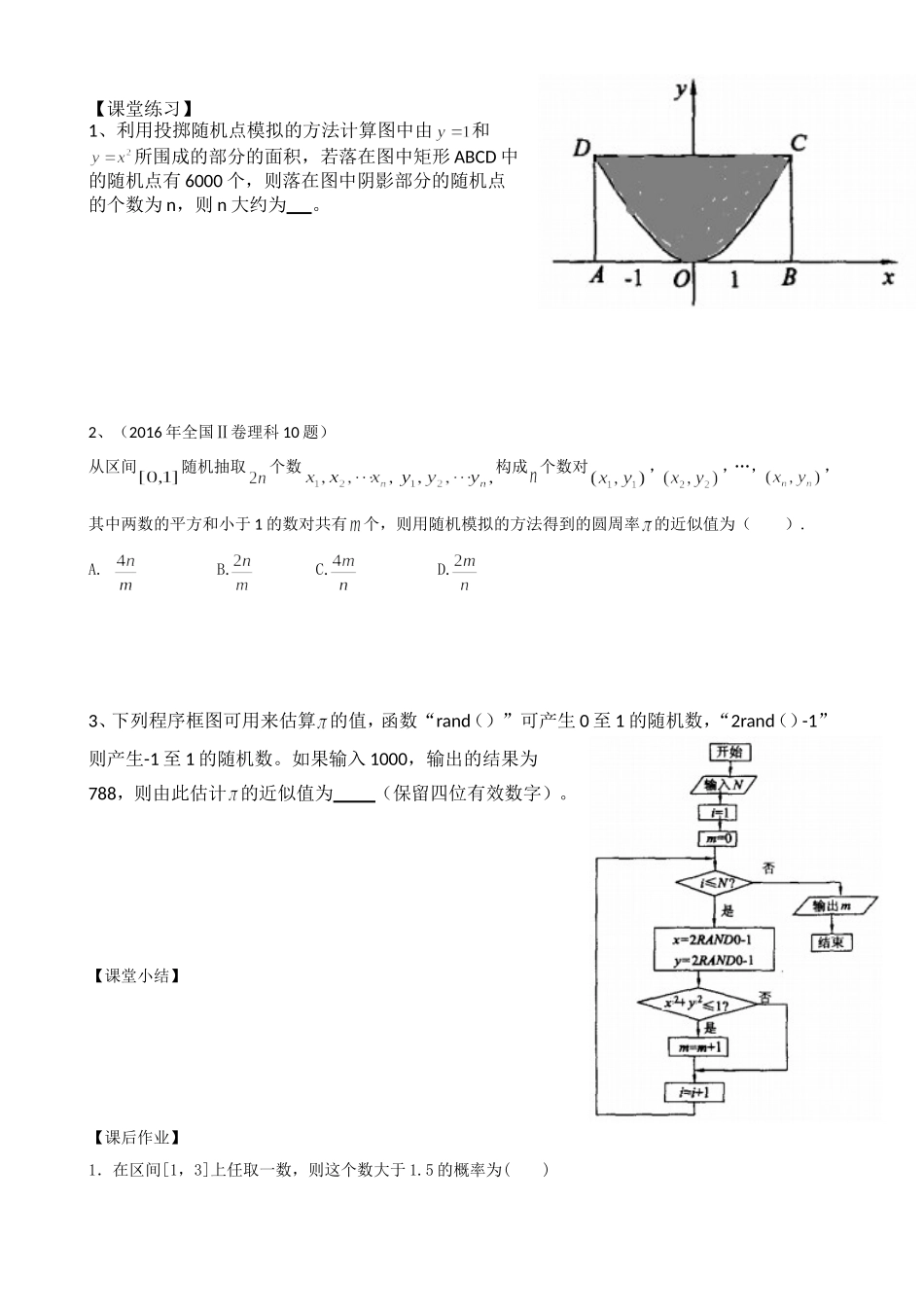
3.3.2均匀随机数的产生学案(人教A版必修3第三章)【学习目标】会利用均匀随机数解决具体的有关概率的问题,理解随机模拟的基本思想是用频率估计概率.【学习重点】1、掌握[0,1]上均匀随机数的产生及[a,b]上均匀随机数的产生.2、学会采用适当的随机模拟法去估算未知量.【学习难点】如何把未知量的估计问题转化为随机模拟问题.【引例】某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.在本题中,打开收音机的时刻X是随机的,可以是0~60之间的任何时刻,并且是等可能的,我们称X服从[0,60]上的均匀分布,X为[0,60]的均匀随机数。【课前自主预习探究】【例1】假设你家订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00—8:00之间,问你父亲在离开家前能得到报纸(称为事件A)的概率是多少?解:送报时间X是0~1之间的均匀随机数;父亲离开家的时间Y也是0~1之间的均匀随机数。若Y+7>X+6.5,即X-Y<0.5,那么父亲在离开家前能得到报纸。具体操作如下:第一步:在A1,B1单元格输入“=rand()”产生两个[0,1]的均匀随机数X,Y;第二步:在C1单元格输入“=A1-B1”,计算出X-Y的值;第三步:同时选中A1,B1,C1,拖曳产生100组数据;第四步:在D1单元格输入“=FREQUENCY(C:C,0.5)”,统计出这D栏数据中小于0.5的数据个数,并计算得出父亲在离开家前能得到报纸的频率(与概率进行比较)。【小组合作探究】根据所给图形,设计一个能用Excel表格进行随机模拟,估计阴影部分面积的方案。要求:1、小组合作完成;2、设计出方案,写出关键步骤,拍照上传(6分钟)图①-圆图②-抛物线部分图像【步骤】【步骤】【深入思考】1、根据图①,你还能设计出估计其他未知量的方案吗?2、根据图②设计出的方案,模拟出面积的近似值,你有什么办法验证?r=1【课堂练习】1、利用投掷随机点模拟的方法计算图中由和所围成的部分的面积,若落在图中矩形ABCD中的随机点有6000个,则落在图中阴影部分的随机点的个数为n,则n大约为。2、(2016年全国Ⅱ卷理科10题)从区间随机抽取个数构成个数对,,…,,其中两数的平方和小于1的数对共有个,则用随机模拟的方法得到的圆周率的近似值为().A.B.C.D.3、下列程序框图可用来估算的值,函数“rand()”可产生0至1的随机数,“2rand()-1”则产生-1至1的随机数。如果输入1000,输出的结果为788,则由此估计的近似值为(保留四位有效数字)。【课堂小结】【课后作业】1.在区间[1,3]上任取一数,则这个数大于1.5的概率为()A.0.25B.0.5C.0.6D.0.752.如图,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为,则阴影区域的面积约为()A.B.C.D.无法计算3、一只蜜蜂在一个棱长为3的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个表面距离大于1,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为()A.B.C.D.4.(2012年陕西理科10题)右图是用模拟方法估计圆周率的程序框图,表示估计结果,则途中空白框内应填入()A.B.C.D.5、若,则事件A与B的关系是()A.互斥不对立B.对立不互斥C.互斥且对立D.以上答案都不对.6、甲、乙两艘轮船都要在某个泊位停靠6小时,假定他们在一昼夜的时间段中随机地到达,试求这两艘船中至少有一艘在停靠泊位时必须等待的概率为.7、(2010年全国新课标卷理科13题)设为区间上的连续函数,且恒有,可以用随机模拟方法近似计算积分,先产生两组(每组个)区间上的均匀随机数和由此得到个点,再数出其中满足的点数,那么由随机模拟方案可得积分的近似值为_____.