探究判定三角形相似的第一个定理VIP免费

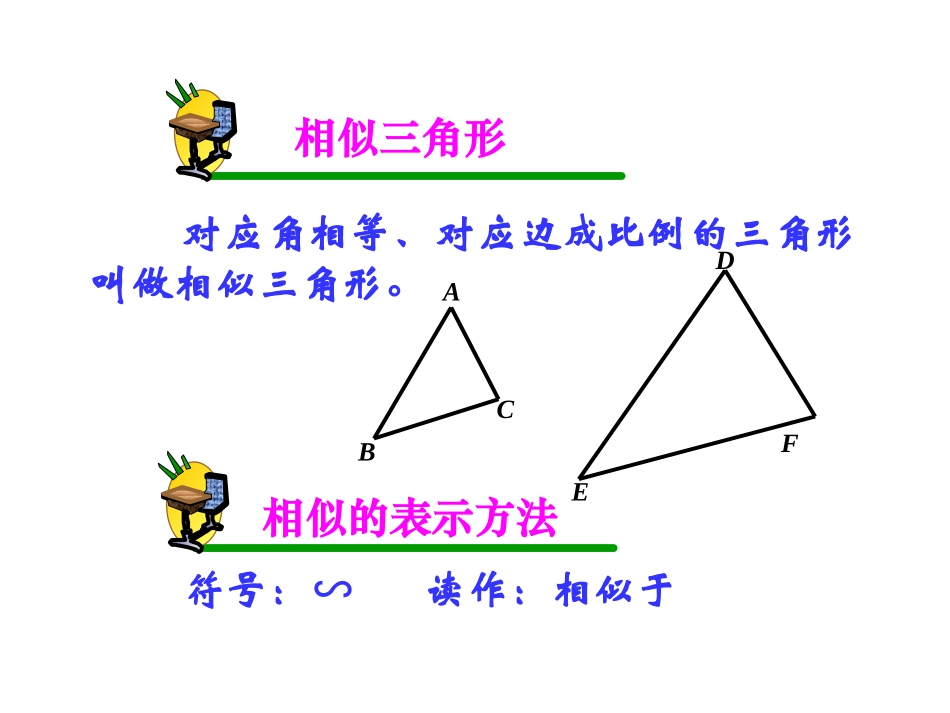
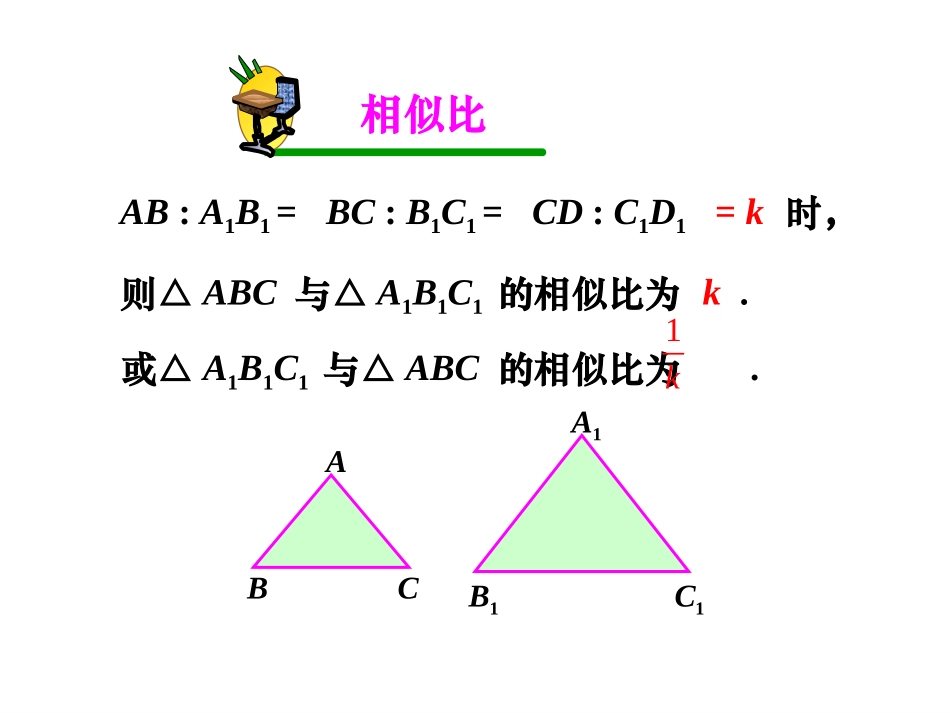
新课导入新课导入新课导入新课导入ABCA1B1C1∠A=∠A1，∠B=∠B1，∠C=∠C1，AB:A1B1=BC:B1C1=CD:C1D1=k当时，则△ABC与△A1B1C1相似，记作△ABC∽△A1B1C1。要把表示对应角顶点的字母写在对应的位置上。注意相似三角形对应角相等、对应边成比例的三角形叫做相似三角形。ABCEDF相似的表示方法符号：∽读作：相似于相似比AB:A1B1=BC:B1C1=CD:C1D1=k时，ABCA1B1C1则△ABC与△A1B1C1的相似比为k.或△A1B1C1与△ABC的相似比为.1k这两个风筝图形相似，观察并思考：ABAA1B1C1大胆猜想，那么，若已知ABA∥1B1，能否得出△ABC1∽△A1B1C1ABA∥1B1除了根据相似三角形的定义来判断是否相似，还有其它的方法吗？教学目标教学目标教学目标教学目标•理解相似三角形的判定方法．知识与能力•以问题的形式，创设一个有利于学生动手和探究的情境，达到学会本节课所学的相似三角形的判定方法．过程与方法•培养学生积极的思考、动手、观察的能力，使学生感悟几何知识在生活中的价值．情感态度与价值观教学重难点教学重难点教学重难点教学重难点•会应用相似三角形的两个判定方法。•怎样选择合格的判定方法来判定两个三角形相似。•抓住判定方法的条件，通过已知条件的分析，把握图形的结构特点。已知：DE//BC，且D是边AB的中点，DE交AC于E.猜想：△ADE与△ABC有什么关系?并证明。ABCDE证明:且∠A=A∠ DE//BC∴∠1=B∠，∠2=C∠∴△ADE与△ABC的对应角相等相似。12三角形的中位线截得的三角形与原三角形相似，相似比。∴四边形DBFE是平行四边形∴DE=BF,DB=EF∴△ADE∽ABC△ABCDEF过E作EF//AB交BC于F又 DE//BC又 AD=DB∴AD=EF ∠A=3∠，∠2=C∠∴△ADEEFC≌△∴DE=FC=BF，∴∴∴△ADE与△ABC的对应边成比例23AE=EC12AEAC12DEBC12ADAEDEABACBC12已知：DE//BC，△ADE与△ABC有什么关系?猜想：△ADE与△ABC有什么关系?相似。ABCDEF当点D在AB上任意一点时，上面的结论还成立吗？12你能证明吗？平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。知识要点知识要点平行于三角形一边的定理ABCDE即：在△ABC中，如果DEBC∥，那么△ADEABC∽△A型你还能画出其他图形吗？平行于三角形一边的直线截其它两边，所得的对应线段成比例。推论ABCDE即：在△ABC中，如果DEBC∥，那么,ADAEDEABACBC,ADAEDBEC,DBECADAE,ABACBCADAEDE（上比全，全比上）（上比下，下比上）（下比全，全比下）DBECABAC，,ABACDBECABCDE相似具有传递性△ADEABC∽△MN如果再作MN∥DE，共有多少对相似三角形？△AMNADE∽△△AMNABC∽△共有三对相似三角形。定义判定方法全等三角形相似三角形回顾并思考三角、三边对应相等的两个三角形全等三角对应相等,三边对应成比例的两个三角形相似角边角ASA角角边AAS边边边SSS边角边SAS斜边与直角边HL判定三角形相似，是不是也有这么多种方法呢？边边边SSS已知：△ABC∽△A1B1C1.A1B1C1ABC111111.ABBCACABBCAC求证：有效利用判定定理一去求证。探究1证明：在线段（或它的延长线）上截取，过点D作，交于点E根据前面的定理可得.11AB1ADAB11DEBC∥11AC1111ADEABC∽A1B1C1ABCDE11111111ADAEDEABBCAC1111111,ABBCACADABABBCAC1AEAC,DEBC111ABCABC∽1ADEABC≌∴又A1B1C1ABCDE∴111111111,AEDEBCACBCBCACAC∴∴（SSS）1111ADEABC∽ ∴如果两个三角形的三组对应边的比相等，那么这两个三角形相似。知识要点知识要点判定三角形相似的定理之一△ABC∽△A1B1C1.111111,ABBCACABBCAC即：如果那么A1B1C1ABC三边对应成比例，两三角形相似。边边边SSS√ABBCACADDEAE，求证：∠BAD=CAE∠。ADCEB∴ΔABCΔ∽ADE∴∠BAC=∠DAE∴∠BAC－∠DAC=∠DAE－∠DAC即∠BAD=CAE∠小练习小练习已知：解： ABBCACADDEAE，边角边SAS探究2已知：△ABC∽△A1B1C1.A1B1C1ABC1111,ABBCkABBC求证：∠B=∠B1.你能证明吗？如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。知识要点知识要点判定三角形相似的定理之二两边对应成比例，且夹角相等，两三角形相似。边角边SAS√A1B1C1ABC△ABC∽△A1B1C1...