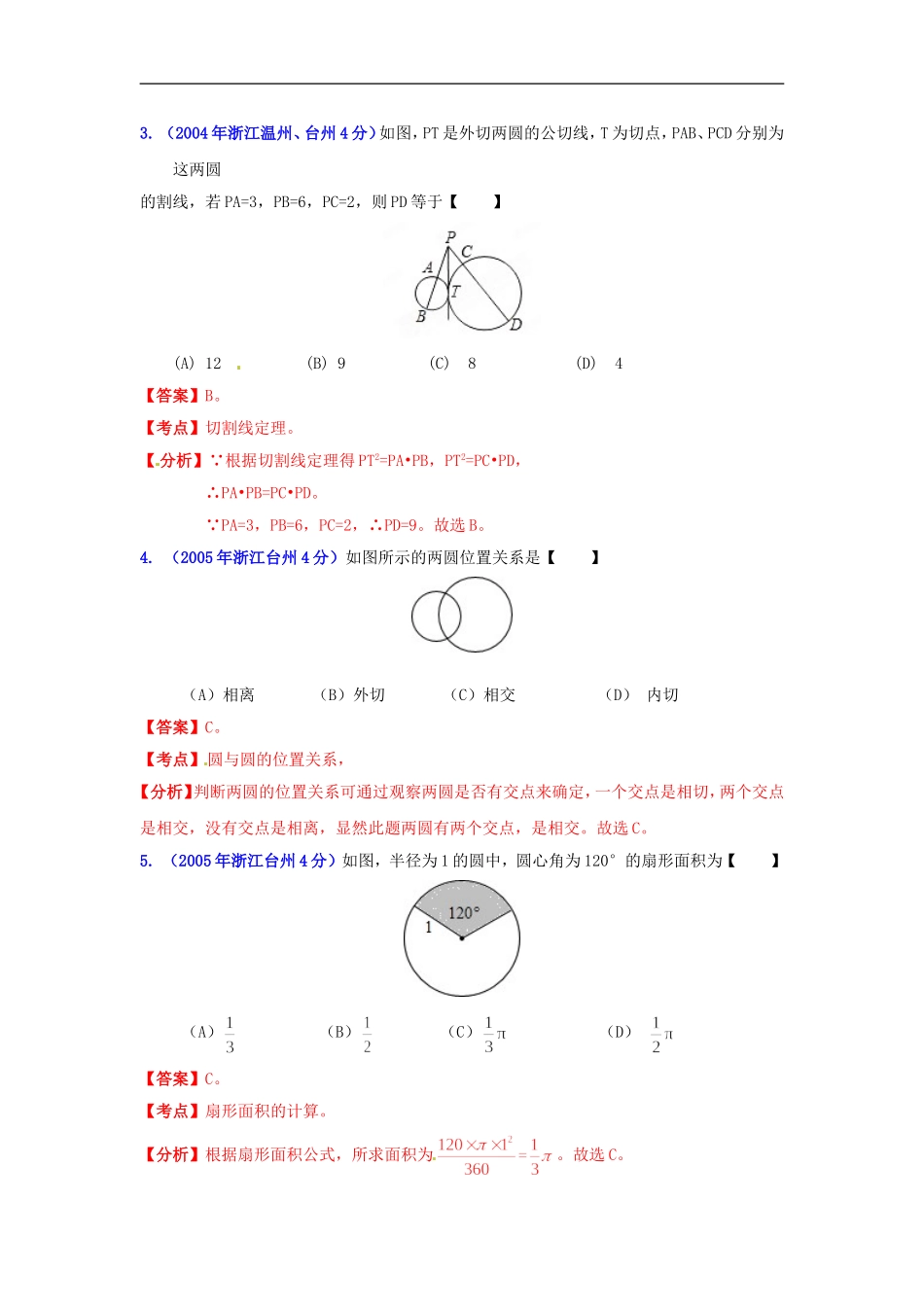
台州市2002-2013年中考数学试题分类解析专题11:圆一、选择题1.(2002年浙江台州4分)如图,⊙O的两条割线PAB,PCD分别交⊙O于点A,B和点C,D.已知PA=6,AB=4,PC=5,则CD=【】(A)(B)(C)7(D)24【答案】C。【考点】相交弦定理。【分析】 ⊙O的两条割线PAB,PCD分别交⊙O于点A,B和点C,D,∴。 PA=6,AB=4,PC=5,∴,解得:CD=7。故选C。2.(2003年浙江台州4分)如图,四个半径均为R的等圆彼此相切,则图中阴影部分(形似水壶)图形的面积为【】A、B、C、D、【答案】A。【考点】相切圆的性质,正方形的判定和性质,扇形面积。【分析】求得四条弧围成的图形的面积然后加上一个圆的面积即可求解:四条弧围成的图形的面积是:以2R为边长的正方形面积减去1个圆满的面积:2R·2R-πR2=4R2-πR2;圆的面积是:πR2。∴图中阴影部分(形似水壶)图形的面积为4R2-πR2+πR2=4R2。故选A。3.(2004年浙江温州、台州4分)如图,PT是外切两圆的公切线,T为切点,PAB、PCD分别为这两圆的割线,若PA=3,PB=6,PC=2,则PD等于【】(A)12(B)9(C)8(D)4【答案】B。【考点】切割线定理。【分析】 根据切割线定理得PT2=PA•PB,PT2=PC•PD,∴PA•PB=PC•PD。 PA=3,PB=6,PC=2,∴PD=9。故选B。4.(2005年浙江台州4分)如图所示的两圆位置关系是【】(A)相离(B)外切(C)相交(D)内切【答案】C。【考点】圆与圆的位置关系,【分析】判断两圆的位置关系可通过观察两圆是否有交点来确定,一个交点是相切,两个交点是相交,没有交点是相离,显然此题两圆有两个交点,是相交。故选C。5.(2005年浙江台州4分)如图,半径为1的圆中,圆心角为120°的扇形面积为【】(A)(B)(C)(D)【答案】C。【考点】扇形面积的计算。【分析】根据扇形面积公式,所求面积为。故选C。6.(2005年浙江台州4分)如图,PA、PB是⊙O的切线,A、B为切点,OP交AB于点D,交⊙O于点C,在线段AB、PA、PB、PC、CD中,已知其中两条线段的长,但还无法计算出⊙O直径的两条线段是【】(A)AB、CD(B)PA、PC(C)PA、AB(D)PA、PB【答案】D。【考点】勾股定理,垂径定理,切割线定理,射影定理,切线长定理。【分析】根据有关定理逐一作出判断:A、连接OA,构造一个由半径、半弦、弦心距组成的直角三角形,根据垂径定理以及勾股定理即可计算。B、延长PO交圆于另一点E,根据切割线定理即可计算。C、首先根据垂径定理计算AD的长,再根据勾股定理计算PD的长,连接OA,根据射影定理计算OD的长,最后根据勾股定理即可计算其半径。D、根据切线长定理,得PA=PB.相当于只给了一条线段的长,无法计算出半径的长。故选D。7.(2006年浙江台州4分)直径所对的圆周角是【】(A)锐角(B)直角(C)钝角(D)无法确定【答案】B。【考点】圆周角定理。【分析】直接根据直径所对的圆周角是直角得出结论。故选B。8.(2006年浙江台州4分)如图,已知⊙O中,弦AB,CD相交于点P,AP=6,BP=2,CP=4,则PD的长是【】(A)6(B)5(C)4(D)3【答案】D。【考点】相交弦定理。【分析】 ⊙O中,弦AB,CD相交于点P,∴。 ,AP=6,BP=2,CP=4,∴,解得PD=3。故选D。9.(2006年浙江台州4分)我们知道,“两点之间线段最短”,“直线外一点与直线上各点连结的所有线段中,垂线段最短”.在此基础上,人们定义了点与点的距离,点到直线的距离.类似地,若点P是⊙O外一点(如图),则点P与⊙O的距离应定义为【】(A)线段PO的长度(B)线段PA的长度(C)线段PB的长度(D)线段PC的长度【答案】B。【考点】新定义。【分析】根据前面的几个定义都是点到图形的最小的距离,因而由图可知:点P到⊙O的距离是线段PA的长度。故选B。10.(2008年浙江台州4分)下列命题中,正确的是【】①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③900的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等A.①②③B.③④⑤C.①②⑤D.②④⑤所以正确的是③④⑤。故选B。11.(2009年浙江台州4分)大圆半径为6,小圆半径为3,两圆圆心距为10,则这两圆的位置关系为【】A.外离B.外切C.相交D.内含...